Пуассоновский процесс
Рассмотрим бесконечно малый промежуток времени Dt (Dt®0), проходящий между моментами t и t+Dt. При определении пуассоновского процесса используются три основные предпосылки:
1. вероятность одного поступления в течение времени Dt определяется в виде: lDt+О(Dt), где О(Dt) – члены более высокого порядка, которыми мы можем пренебречь при Dt®0;
2. вероятность нулевого поступления в течение времени Dt равна 1-lDt;
3. поступление – без последействия (без памяти), т.е. поступление в течение Dt не зависит от предыдущих поступлений.
Если теперь рассмотреть большой промежуток времени Т, то вероятность p(k) того, что в промежутке Т произойдут k поступлений, равна:
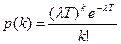, где k = 0, 1, 2, …
Это равенство называется распределением Пуассона. Оно нормировано:
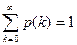
и его среднее значение имеет вид:
.
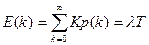Дисперсия распределения:
.
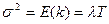Теперь рассмотрим большой промежуток времени и отметим на нём моменты, в которые наступили события Пуассоновского процесса.
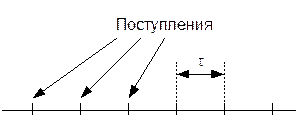
Очевидно, что t - это положительная случайная величина с непрерывным распределением. Оказывается, что для Пуассоновского распределения величина t распределена по показательному закону:
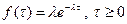
Среднее значение показательного распределения:
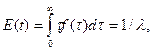
а дисперсия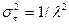 
.
Рассмотрим очередь из нескольких вызовов, ожидающих обслуживания. Отметим время завершения обслуживания:
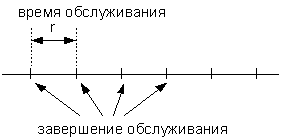
Обозначим случайную величину, описывающую время между завершениями обслуживания через r. Эта же величина является временем обслуживания. Если r распределена по показательному закону со средним значением
E(r)=1/m,
то плотность распределения будет равна:
.
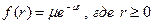Процесс обслуживания является полным аналогом процесса поступления и обладает всеми свойствами последнего. На основании этого вероятность завершения обслуживания в малом промежутке времени (t, t+Dt) в точности равна mDt + О(Dt), а вероятность незавершения обслуживания в промежутке (t, t+Dt) равна 1-mDt+О(Dt) независимо от предыдущих или последующих завершений.
Показательная модель обслуживания обладает свойством отсутствия последействия, которая используется как одна из определяющих предпосылок Пуассоновского процесса.
Ещё одно полезное свойство, объединяющее одну из причин, по которой Пуассоновский процесс часто используется для моделирования входящих потоков, заключается в том, что при объединении m независимых Пуассоновских потоков с произвольными интенсивностями l1, l2, … lm, объединённый поток также будет Пуассоновским с интенсивностью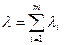 
.
В применении к сетям такое положение возникает, когда статистически объединяются пакеты иди вызовы от ряда источников, каждый из которых генерирует их с Пуассоновской интенсивностью.
Система обслуживания М/М/1
Система обслуживания М/М/1 – это система с одной обслуживающей линией, Пуассоновским входящим потоком, показательным распределением обслуживания и дисциплиной ОПП (обслуживание в порядке поступления).
Диаграмма изменений состояний во времени для системы может быть изображена следующим образом:
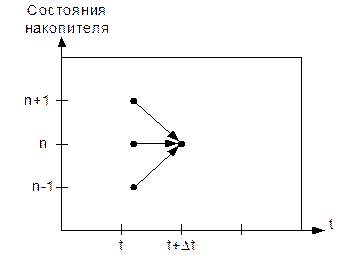
Пусть процессы поступления и обслуживания определяются соответственно параметрами l и m. Определим вероятность pn(t+Dt) того, что в момент времени t+Dt в системе будет находиться n клиентов (пакетов или вызовов). Из диаграммы видно, что в момент времени t система могла находиться только в состоянии n-1, n или n+1. Тогда мы можем записать:
.
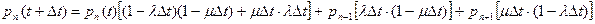Вероятности перехода из одного состояния в другое получены в результате рассмотрения путей, по которым происходят эти переходы, и расчёта соответствующих вероятностей. Например, если система осталась в состоянии n, то могли произойти либо уход и одно поступление с вероятностью mDt, либо ни одного ухода или поступления с вероятностью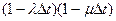 
, что и показано в первом случае.
Производя упрощения, иcпользуя разложение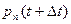 
в ряд Тейлора, можно получить следующее уравнение:
.
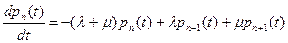Для стационарного состояния вероятность pn(t) приближается к некоторому постоянному значению, поэтому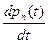 
= 0. Тогда последнее уравнение для стационарного случайного процесса упрощается и принимает вид:
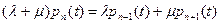(1).
Форма уравнения (1) показывает, что при работе системы действует стационарный принцип равновесия: левая часть описывает интенсивность уходов из состояния n, а правая часть – интенсивность приходов в состояние n из n-1 или n+1. Чтобы существовали вероятности стационарного состояния, эти две интенсивности должны быть равны.
Рассмотрим диаграмму состояний для системы М/М/1
Ввиду предположений о Пуассоновском процессе поступления и уходов клиентов переходы имеют место только между соседними состояниями с показанными интенсивностями.
Уравнение (1) может быть решено несколькими способами. При простейшем их них может быть использовано условие равновесия. Если рассчитать общий «поток вероятности», пересекающий границу области 1, и приравнять исходящий поток к входящему, получиться уравнение (1). Область 2 охватывает всё множество точек от 0 до n. Поток, поступающий в эту область, равен mpn+1, а поток, покидающий её, равен lpn. Приравнивая эти два потока, получим: mpn+1=lpn. Повторяя последнее уравнение n раз, получим:
mpn=lpn-1; mp2=lp1;
…
mp3=lp2; mp1=lp0;
Следовательно,
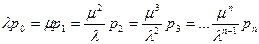
Отсюда:
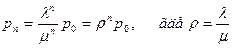
Значение р0 для случая бесконечной очереди можно найти, используя нормирующее условие: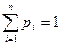 
. Просуммировав n вышеприведенных уравнений и учитывая нормировку, получим:
.
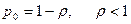Используя это, можно записать решение для установившегося режима:
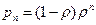. (2)
Распределение вероятностей (2) системы М/М/1 называется геометрическим распределением.
Обобщим результаты для случая конечной очереди, вмещающей не более N пакетов. Можно показать, то в этом случае:
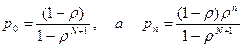
В частности, вероятность того, что очередь заполнена, совпадает с вероятностью блокировки:
.
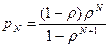На следующем рисунке приведён график вероятности блокировки в зависимости от нормированной нагрузки r.
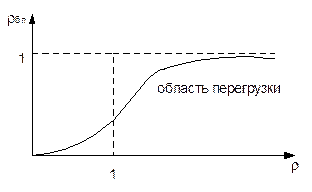
Область r>1 называется областью перегрузки или скученности. Производительность системы, которая близка к нагрузке l при малых r, выравнивается и при возрастании r приближается к пропускной способности m.
Рассмотрим область r<1. На основании определения среднего значения pn, проведя суммирование, получим среднее число E(n) клиентов в системе, включая находящихся на обслуживании:
.
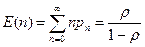Это отражено на следующем рисунке:
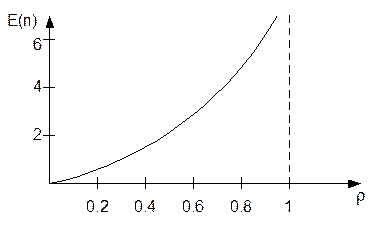
При увеличении r среднее число клиентов в очереди резко возрастает за счёт (1-r) в знаменателе.
Можно заметить, что при росте нагрузки системы растёт её производительность, однако при этом блокируется всё большее количество клиентов, а следовательно, растёт E(n), что ведёт к увеличению времени задержки в очереди.
Для нахождения времени задержки используют формулу Литтла:
lE(T) = E(n), где E(T) – среднее время задержки в системе.
Для системы М/М/1, используя предыдущие формулы, можно получить: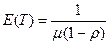 
.
Дата добавления: 2015-07-30; просмотров: 1371;