ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Особая значимость двоичной системы счисления в информатике определяется тем, что внутреннее представление любой информации в компьютере является двоичным, т.е. описываемым наборами только из двух знаков (0 и 1).
Конкретизируем описанный выше способ в случае перевода чисел из десятичной системы в двоичную. Целая и дробная части переводятся порознь. Для перевода целой части (или просто целого) числа необходимо разделить ее на основание системы счисления и продолжать делить частные от деления до тех пор, пока частное не станет равным 0. Значения получившихся остатков, взятые в обратной последовательности, образуют искомое двоичное число. Например:
Остаток
25 : 2 = 12 (1),
12 : 2 = 6 (0),
6 : 2 = 3 (0),
3 : 2 = 1 (1),
1 : 2 = 0 (1).
Таким образом
25(10)=11001(2).
Для перевода дробной части (или числа, у которого «0» целых) надо умножить ее на 2. Целая часть произведения будет первой цифрой числа в двоичной системе. Затем, отбрасывая у результата целую часть, вновь умножаем на 2 и т.д. Заметим, что конечная десятичная дробь при этом вполне может стать бесконечной {периодической) двоичной. Например:
0,73 • 2 = 1,46 (целая часть 1),
0,46 • 2 = 0,92 (целая часть 0 ),
0,92 • 2 = 1,84 (целая часть 1),
0,84 • 2 = 1,68 (целая часть 1) и т.д.
В итоге
0,73(10) =0,1011...(2).
Над числами, записанными в любой системе счисления, можно; производить различные арифметические операции. Так, для сложения и умножения двоичных чисел необходимо использовать табл. 1.5.
Таблица 1.5. Таблицы сложения и умножения в двоичной системе
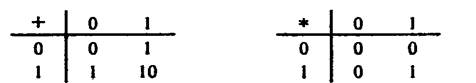
Заметим, что при двоичном сложении 1 + 1 возникает перенос единицы в старший разряд - точь-в-точь как в десятичной арифметике:
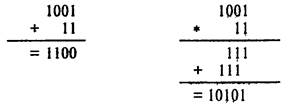
Дата добавления: 2015-07-30; просмотров: 807;
