Напряжение на участке цепи

Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.

На рис. 7 изображён участок цепи, на котором есть сопротивление 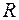, и нет ЭДС. Крайние точки этого участка обозначены буквами аи в. Пусть ток течёт от точки а к точке в.

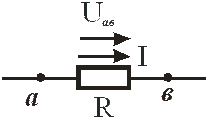
Рис. 7

На участке цепи без ЭДС ток течёт от более высокого потенциала к более низкому. Следовательно, потенциал точки а ( 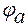) выше потенциала точки в( 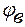) на величину, равную произведению тока на сопротивление :

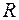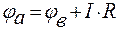. (5)

В соответствии с определением напряжения между точками а и в

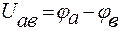. (6)

Следовательно, 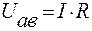. (7)

Другими словами, напряжение на сопротивлении равно произведению тока, протекающего по сопротивлению, на величину этого сопротивления.

В электротехнике разность потенциалов на концах сопротивления принято называть либо ”напряжение на сопротивлении”, либо ”падением напряжения”. Положительное направление падения напряжения совпадает с положительным направлением тока, протекающего по данному сопротивлению. Положительное направление напряжения указывают на схемах стрелкой, Стрелка должна быть направлена от первой буквы индекса ко второй. Так, положительное направление напряжения 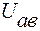изобразится стрелкой, направленной от ак в.

Рассмотрим теперь вопрос о напряжении на участке цепи, содержащем не только сопротивление, но и ЭДС.

На рис. 8, а и впоказаны участки некоторых цепей, по которым протекает ток . Найдём разность потенциалов (напряжение) между точками а исдля этих участков.

По определению

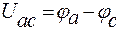. (8)

Рис. 8

Выразим потенциал точки а через потенциал точки с. При переходе от точки ск точке в (рис. 8, а) идём встречно ЭДС Е, поэтому потенциал точки в оказывается ниже потенциала точки с на величину ЭДС Е, т.е.

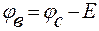. (9)

Для рис. 8, б при перемещении от точки с к точке в идём согласно ЭДС Е и поэтому потенциал точки в оказывается выше потенциала точки с на величину ЭДС Е, т.е.

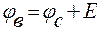. (10)

Ранее говорилось, что на участке цепи без ЭДС ток течёт от более высокого потенциала к более низкому. Поэтому в обеих схемах рис. 8 потенциал точки а выше потенциала точки в на величину падения напряжения на сопротивлении R:

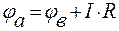. (11)

Таким образом, для рис. 8, а имеем

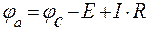, или

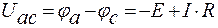, (12)

и для рис. 8, б имеем

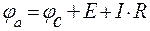, или

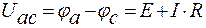. (13)

Из самого определения напряжения следует также, что 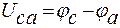, поэтому 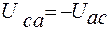. Другими словами, изменение чередования индексов равносильно изменению знака этого напряжения. Из изложенного ясно, что напряжение может быть и положительной, и отрицательной величиной.