Основные формулы и законы. где – постоянная Планка; – импульс частицы ( – масса частицы; – её скорость).

· Длина волны де Бройля

,

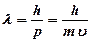где 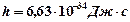– постоянная Планка; 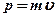– импульс частицы ( 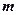– масса частицы; 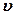– её скорость).

· Связь импульса частицы 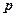с ее кинетической энергией :

,

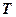где 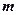– масса покоя частицы. При малых скоростях .

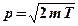· Соотношение неопределенностей Гейзенберга

,

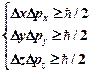
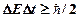где 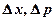, 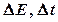– соответственно неопределенности координаты, импульса, энергии и времени, .

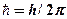· Нестационарное уравнение Шредингера

.

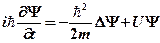· Уравнение Шредингера для стационарных состояний

,

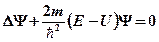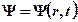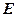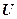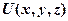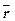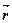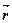
где – волновая функция микрочастицы; – полная энергия микрочастицы; = – потенциальная энергия частицы; – пространственная координата ( = 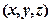); t – время, ∆ = 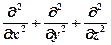– оператор Лапласа (записан в декартовых координатах); 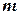– масса микрочастицы; 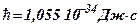– постоянная Планка; 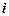= 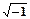– мнимая единица.

· Одномерное уравнение Шредингера для стационарных состояний

.

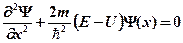· Условие нормировки волновой функции

.

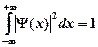
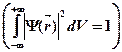· Плотность вероятности

,

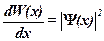
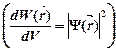где 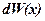– вероятность того, что частица может быть обнаружена вблизи точки с координатой 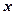на участке .

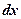· Вероятность обнаружения частицы в интервале от 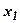до

.

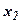
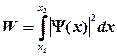· Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика шириной 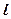(0 ≥ ≥ )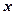

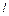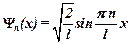(собственная нормированная волновая функция)

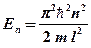(собственное значение энергии),

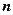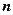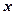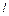
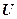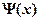где – главное квантовое число ( = 1, 2, 3,…). В области 0≥ ≥ = ∞ и = 0.

· Коэффициент прозрачности прямоугольного потенциаль-ного барьера

,

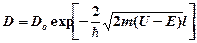где 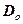– постоянный множитель (можно приравнять единице); 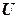– высота барьера; 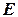– полная энергия частицы; 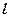– ширина барьера.

· Энергия квантового осциллятора

,

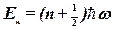где 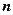– главное квантовое число ( 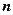=0, 1, 2,…); 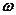– собственная частота колебаний осциллятора.

· Для частиц с целочисленными спинами (бозонов) справедлива статистика Бозе-Эйнштейна, а для частиц с полуцелыми спинами (фермионов) справедлива статистика Ферми-Дирака. Обобщенное уравнение для квантовых статистик

,

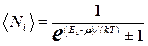где 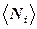- среднее число частиц в состоянии с номером i,
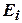– энергия частицы в этом состоянии; m – так называемый химический потенциал, определяемый из условия 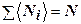, т. е. сумма всех частиц равна полному числу 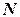частиц в системе, знак минус (-) перед единицей в знаменателе соответствует статистике бозонов (распределению Бозе-Эйнштейна, а знак плюс (+) соответствует статистике фермионов (распределению Ферми-Дирака).