Расчет несимметричного КЗ
1. Составляются схемы замещения прямой, обратной и нулевой последовательностей.
Схема замещения прямой последовательности полностью аналогична схеме замещения для расчета 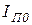 трехфазного КЗ.
трехфазного КЗ.
Схема замещения обратной последовательности такая же, но без ЭДС.
Схема замещения нулевой последовательности зависит от схем соединения обмоток трансформаторов. ЭДС в схеме отсутствуют. Ток нулевой последовательности является по сути однофазным током, протекающим по фазе и замыкающимся через землю. Схему замещения нулевой последовательности начинают строить от точки КЗ (которая как бы является источником токов нулевой последовательности) прослеживая пути протекания тока нулевой последовательности. В схеме замещения нулевой последовательности изменяются сопротивления ВЛ. Пример составления схемы замещения нулевой последовательности приведен на рисунке 6.
Схемы замещения каждой последовательности эквивалентируются так же, как при расчете трехфазного КЗ.
2. Расчет симметричных составляющих токов и напряжений всех последовательностей.
За особую фазу принимаем фазу А, тогда периодическая составляющая тока фазы А прямой последовательности.
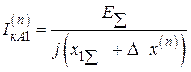 ,
,
где  – эквивалентная ЭДС в схеме прямой последовательности;
– эквивалентная ЭДС в схеме прямой последовательности;
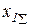 – эквивалентное сопротивление схемы прямой последовательности;
– эквивалентное сопротивление схемы прямой последовательности;
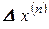 – дополнительное сопротивление, которое определяется видом КЗ (
– дополнительное сопротивление, которое определяется видом КЗ ( 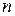 ) и параметрами схем замещения обратной и нулевой последовательностей.
) и параметрами схем замещения обратной и нулевой последовательностей.
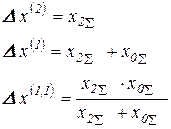
Токи обратной и нулевой последовательностей особой фазы в месте несимметричного КЗ связаны с током прямой последовательности соотношением:
- при двухфазном КЗ
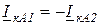
- при однофазном КЗ

- при двухфазном КЗ на землю

Напряжения прямой обратной и нулевой последовательностей особой фазы в месте КЗ
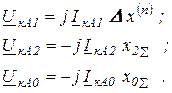
Умножение вектора на 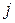 означает его поворот на 90о против часовой стрелки.
означает его поворот на 90о против часовой стрелки.
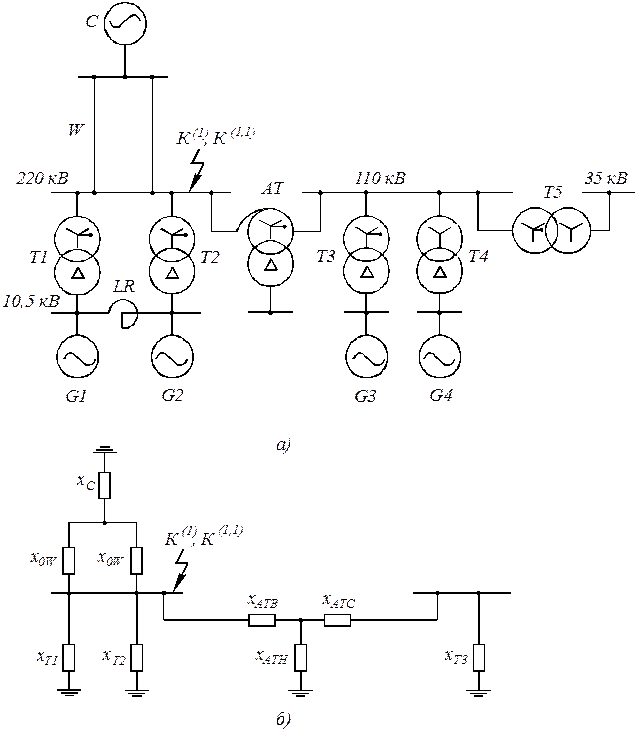
Рисунок 6 – Расчетная схема (а) и схема замещения нулевой последовательности (б).
Модуль тока в поврежденных фазах ( 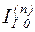 ) при любом виде несимметричного КЗ (п)
) при любом виде несимметричного КЗ (п)
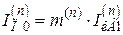 .
.
Коэффициент m:
– при двухфазном КЗ
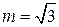 ,
,
– при однофазном КЗ
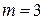 ,
,
– при двухфазном КЗ на землю
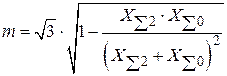 .
.
3. Построение векторной диаграммы.
Из метода симметричных составляющих известно, что

Умножение вектора на оператор 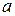 означает его поворот на 120о против часовой стрелки, на
означает его поворот на 120о против часовой стрелки, на 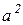 – на 240о.
– на 240о.
Для определения фазной величины нужно геометрически сложить соответствующие симметричные составляющие
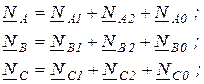
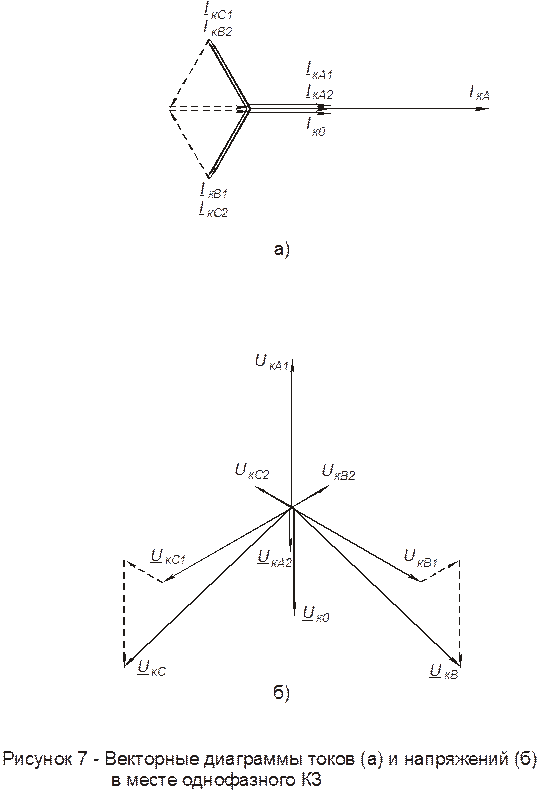
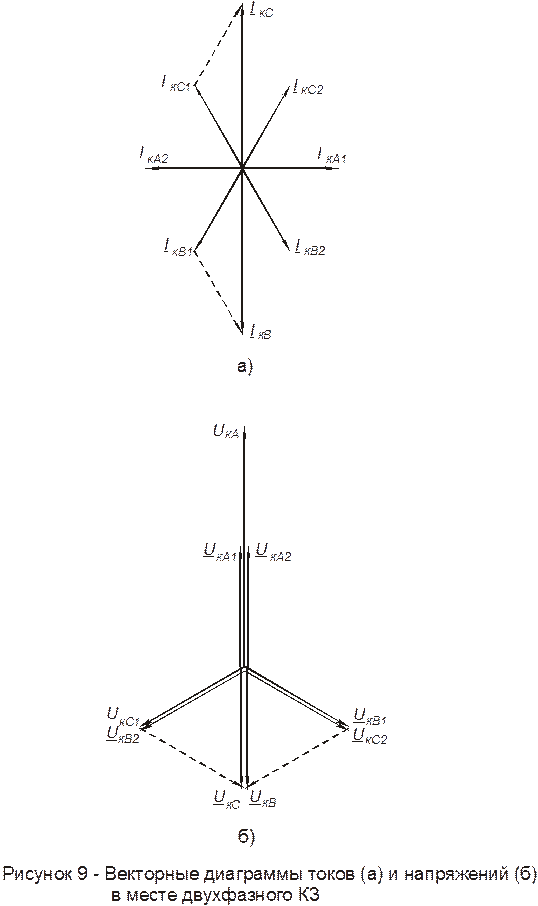
Примеры векторных диаграмм для различных видов КЗ приведены на рисунках 7¸9.

Приложение 1
Эквивалентные преобразования схем.
Путем эквивалентных преобразований схема замещения приводится к простейшему виду. Для этого используются известные методы преобразования линейных электрических цепей.
Преобразование (свертывание) схемы выполняется в направлении от источника питания к месту КЗ.
1. Преобразование последовательной цепи:
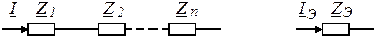 |
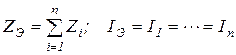
2.
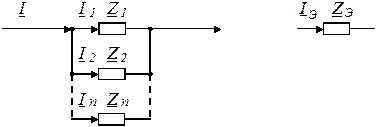 |
Преобразование параллельной цепи:
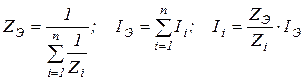 .
.
Если 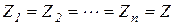 , то
, то
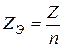
Две параллельные ветви:

3. Преобразование звезды в эквивалентный треугольник и обратно:
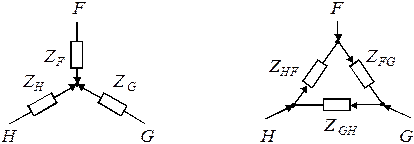 |
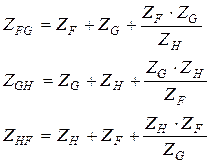

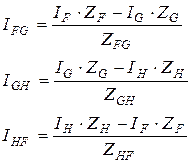
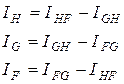
4.
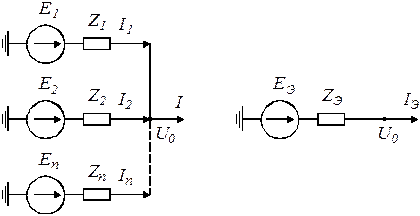 |
Эквивалентирование генераторов
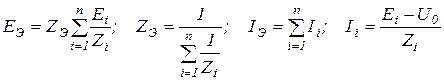
Если 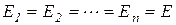 , то
, то 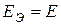
Два генератора:
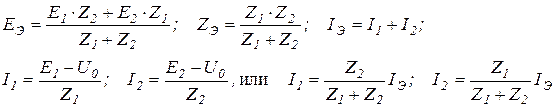
5. 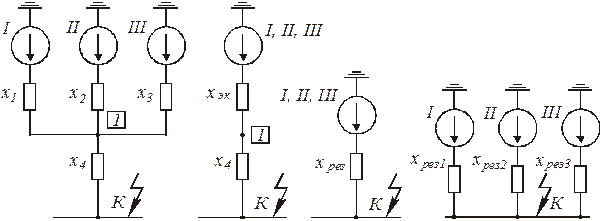 В процессе преобразования схемы замещения часто возникает задача «разделения связанных цепей».
В процессе преобразования схемы замещения часто возникает задача «разделения связанных цепей».
а) б) в) г)
Рисунок 1 - Разделение связанных цепей.
Токи от источников I, II, III проходят через общее сопротивление x4, причем в общем случае число ветвей источников может быть любым. Для того чтобы определить ток, поступающий к точке КЗ от каждого источника, необходимо преобразовать схему к виду, показанному на рисунке 1,г. Расчет производится в следующем порядке.
Определяют результирующее сопротивление схемы (рисунок 1, а–в):
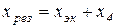 ,
,
где xэк – эквивалентное сопротивление всех источников питания относительно узла 1 схемы:
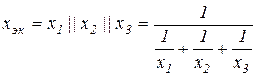 .
.
Принимают относительное значение периодической составляющей тока в месте КЗ за единицу ( 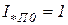 ) и находят коэффициенты распределения, т.е. долю участия в токе КЗ каждого источника. На основании законов Кирхгофа можно записать:
) и находят коэффициенты распределения, т.е. долю участия в токе КЗ каждого источника. На основании законов Кирхгофа можно записать:
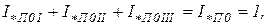
а также
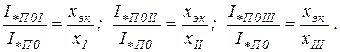
Отсюда коэффициенты распределения по ветвям
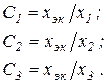
Правильность вычисления коэффициентов можно проверить по выполнению условия
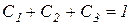 .
.
Учитывая, что токораспределение по ветвям должно оставаться неизменным, получаем (рисунок 1,г)
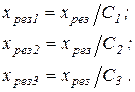
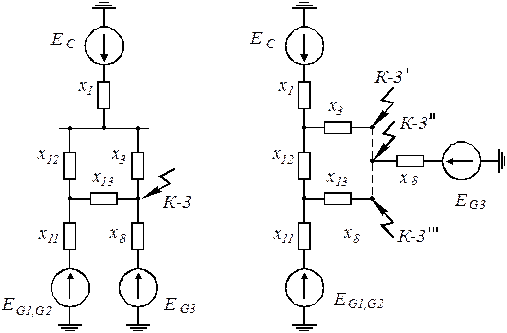
6. Если трехфазное КЗ находится в узле с несколькими сходящимися в нем ветвями (рисунок 2,а), то этот узел можно расчленить, сохранив на конце каждой образовавшейся ветви такое же КЗ (рисунок 2,б).
а) б)
Рисунок 2 - Разрезание узла по точке короткого замыкания.
Далее полученную схему нетрудно преобразовать относительно любой из точек КЗ, учитывая другие ветви с коротким замыканием как обычные нагрузочные ветви с ЭДС, равными нулю.
7. При симметрии схемы замещения относительно точки КЗ или симметрии участка схемы относительно какой-либо промежуточной точки в ходе преобразования можно соединить точки, имеющие одинаковые потенциалы, и исключить из схемы сопротивления, по которым токи КЗ не протекают.
Например, если точка КЗ делит схему на две симметричные равные части (рисунок 3,а), то при одинаковых характеристиках генераторов G1 и G3 и трансформаторов узлы а и б схемы будут иметь одинаковые потенциалы, вследствие чего их можно совместить. В результате получится схема, представленная на рисунке 3,в. В этой схеме 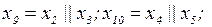
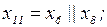
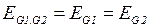 . Дальнейшее преобразование схемы производится по обычным правилам.
. Дальнейшее преобразование схемы производится по обычным правилам.
8. В ряде случаев преобразование схем замещения упрощается, если трехлучевую звезду заменить эквивалентным треугольником, затем разрезать его по вершине, где приложена ЭДС. Образовавшиеся параллельные ветви заменяют эквивалентными с той же ЭДС. Рассмотрим сложную несимметричную схему (рисунок 4,а) и ее схему замещения (рисунок 4,б). Преобразуем звезду сопротивлений ( 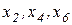 ) в треугольник сопротивлений (
) в треугольник сопротивлений ( 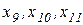 ), как показано на рисунке 5,а. Разрезав треугольник по узлу 1, получаем схему рисунка 5,б. Дальнейшие преобразования схемы приведены на рисунке 5, в, г. Здесь
), как показано на рисунке 5,а. Разрезав треугольник по узлу 1, получаем схему рисунка 5,б. Дальнейшие преобразования схемы приведены на рисунке 5, в, г. Здесь
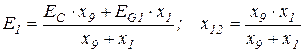 ;
;
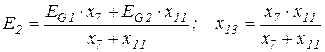 .
.
Получившийся треугольник ( 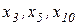 ) преобразуется в звезду (
) преобразуется в звезду ( 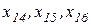 ). После определения сопротивлений
). После определения сопротивлений 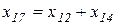 и
и 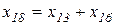 получаем схему, приведенную на рисунке 5,г.
получаем схему, приведенную на рисунке 5,г.
Если генераторы G1 и G2 схемы, приведенной на рисунке 4 имеют одинаковые ЭДС, то их можно объединить в эквивалентную машину с S=2Sном, причем 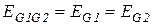 . При таком объединении образуется треугольник сопротивлений (
. При таком объединении образуется треугольник сопротивлений ( 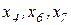 ), который преобразуется в звезду (
), который преобразуется в звезду ( 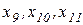 ), как показано на рисунке 6,а. В схеме на рисунке 6,б определяют сопротивления
), как показано на рисунке 6,а. В схеме на рисунке 6,б определяют сопротивления 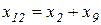 и
и  . Получившийся в результате треугольник (
. Получившийся в результате треугольник ( 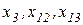 ) преобразуется в звезду (
) преобразуется в звезду ( 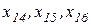 ). После определения сопротивлений
). После определения сопротивлений 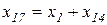 и
и 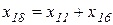 получаем схему, приведенную на рисунке 5,г.
получаем схему, приведенную на рисунке 5,г.

а) б) в)
Рисунок 3 – Короткое замыкание в симметричной сложной схеме.
 |
а) б)
Рисунок 4 – Короткое замыкание в сложной несимметричной схеме.
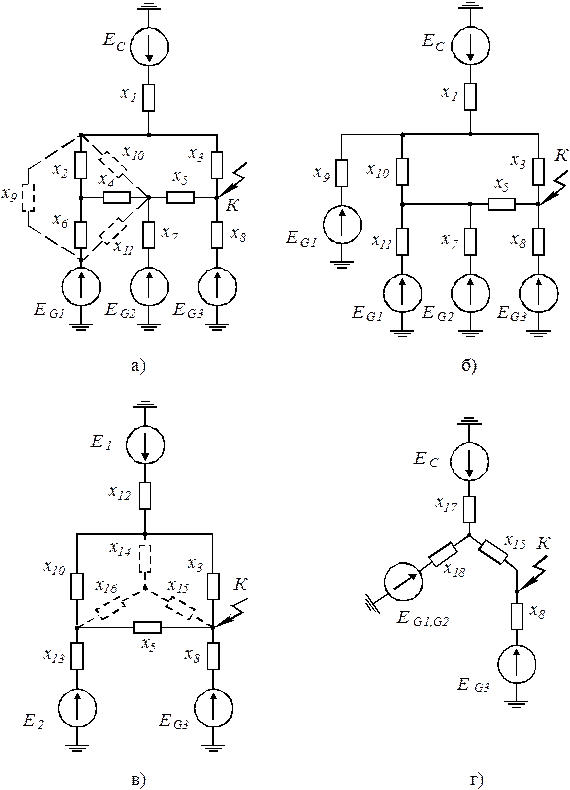
Рисунок 5 – Преобразование сложной схемы.

а) б)
Рисунок 6 – Преобразование сложной схемы по методу треугольник-звезда.
Литература
1. ГОСТ 27514-87. Короткие замыкания в электроустановках. Методы расчета в электроустановках переменного тока напряжением свыше 1 кВ.
2. Винославский В.Н., Пивняк Г.Г., Несен Л.И., Рыбалко А.Я, Прокопенко В.В. Переходные процессы в системах электроснабжения. - Киев.: Выща школа, 1989.
3. Ульянов С.А. Электромагнитные переходные процессы в электрических системах.- М.: Энергия, 1979.
4. Рожкова Л.Д., Козулин В.С. Электрооборудование станций и подстанций. – М.: Энергоатомиздат, 1987.
5. Крючков И.П., Неклепаев Б.Н., Старшинов В.А. и др. Расчет коротких замыканий и выбор электрооборудования: Учеб. Пособие для студ. высш. учеб. заведений.– М.: Издательский центр «Академия», 2005.
6. Рожкова Л.Д., Карнеева Л.К., Чиркова Т.В. Электрооборудование электрических станций и подстанций. – М.: Издательский центр «Академия», 2004.
7. ГОСТ 30323 –95 (ГОСТ Р 50254-92) Короткие замыкания в электроустановках. Методы расчета электродинамического и термического действия тока короткого замыкания– М.: Издательство стандартов, 1996.
Дата добавления: 2015-07-30; просмотров: 3645;
