Кафедра радиоэлектронных средств

Факультет прикладной математики и телекоммуникаций

Лабораторные работы №1,2

«Теоретические основы мобильной связи»

«Исследование свойств псевдослучайных сигналов»

Выполнила:

студентка группы ИКТ-32-3 ____________________/ Шустова Н.С ./

Проверил:

преподаватель кафедры РЭС _______________________/Прозоров Д.Е./

Киров 2013

Цель работы:

ознакомление с методами формирования и корреляционными свойствами широкополосных сигналов.

Оборудование:

персональный компьютер, программа MATLAB.

1.1Построить математическую модель генератора, формирующего первую М-последовательность, соответствующую логической функции: xn=xn−3⊕xn−5 .

Математическая модель изображена на рисунке 1.

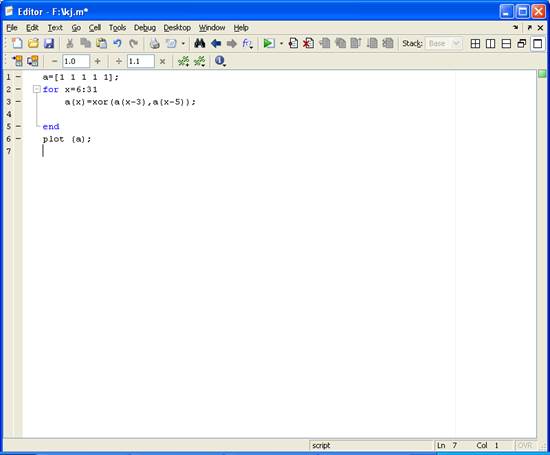
Рисунок 1 – Математическая модель

Результат работы, полученная М-последовательность:

a =

Columns 1 through 18

1 1 1 1 1 0 0 0 1 1 0 1 1 1 0 1 0 1

Columns 19 through 31

0 0 0 0 1 0 0 1 0 1 1 0 0

С помощью функции plot(а) построим график получившейся последовательности (представлен на рисунке 1.1):

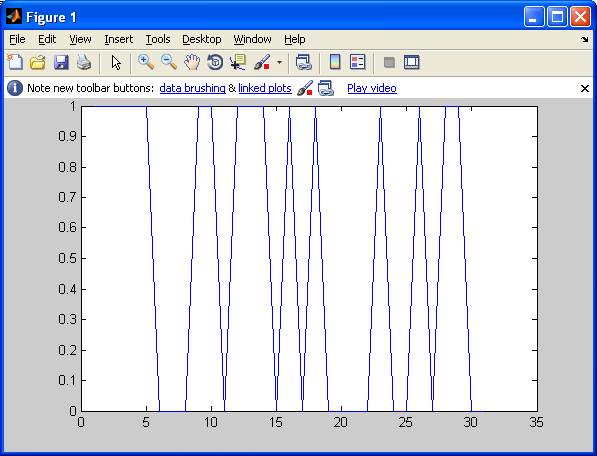
Рисунок 1.1 – График М-последовательности

1.2 Построение графика апериодической АКФ последовательности a(х), изображено на рисунке 1.2.

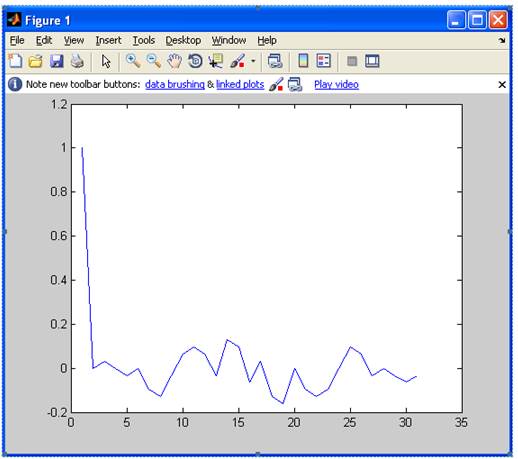
Рисунок 1.2 – Апериодическая АКФ

График построен с помощью кода:

p=[1 1 1 1 1];

L=31;

for t=0:L-1;

p1=a(1+t:L);

p2=a(1:L-t);

A=sum(p1==p2);

D=sum(p1~=p2);

r2(t+1)=(A-D)/L;

end

plot(r2);

Построение графика периодической АКФ, изображено на рисунке 1.3.

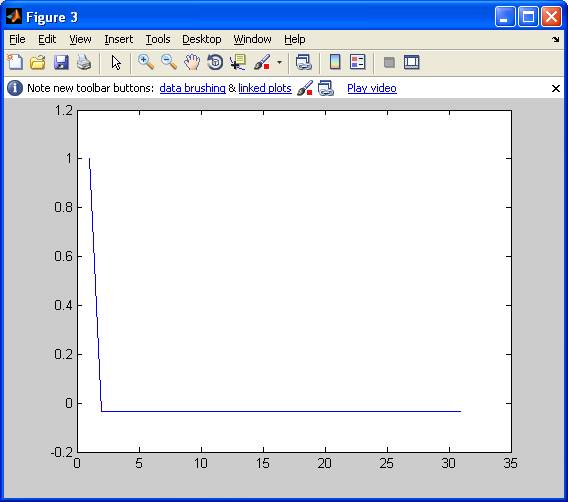
Рисунок 1.3 – Периодическая АКФ

График построен с помощью кода:

a=[p p];

for t=0:L-1;

A=sum(a(t+1:t+L)==p);

D=L-A;

r(t+1)=(A-D)/L;

end

plot(r);

1.3Построение генератора второй М-последовательности, график изображён на рисунке 1.4. Логическая функция:

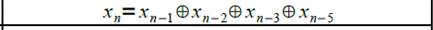
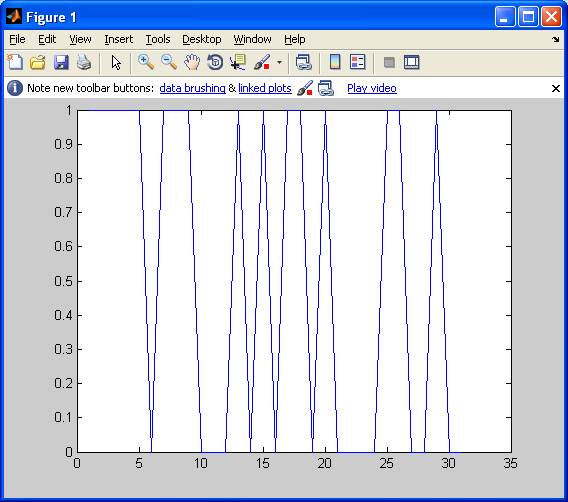
Рисунок 1.4 – График

Код математической модели:

for k=6:L;

p(k)=p(k-1)+p(k-2)+p(k-3)+p(k-5);

p(k)=mod(p(k),2);

end

plot(p);

1.4Построение ВКФ перовой и второй М-последовательностей, график изображен на рисунке 1.5.

Рисунок 1.5 – График ВКФ

График построен с помощью кода:

for t=0:L-1;

p1=a(1+t:L);

p2=b(1:L-t);

A=sum(p1==p2);

D=sum(p1~=p2);

r3(t+1)=(A-D)/L;

end

plot(r3);

3. Построение генератора, формирующего третью М-последовательность.

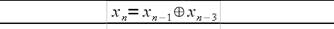
Код, генерирующий данную последовательность:

y=[1 0 1];

for i=4:63

y(i)=xor(y(i-1),y(i-3));

end

Результат работы:

y =

Columns 1 through 18

1 0 1 0 0 1 1 1 0 1 0 0 1 1 1 0 1 0

Columns 19 through 36

0 1 1 1 0 1 0 0 1 1 1 0 1 0 0 1 1 1

Columns 37 through 54

0 1 0 0 1 1 1 0 1 0 0 1 1 1 0 1 0 0

Columns 55 through 63

1 1 1 0 1 0 0 1 1

С помощью функции plot(y) построим график (рисунок 3) получившейся последовательности:

Рисунок 3 – График третьей последовательности

3.1. Построим генератор составной последовательности.

Код, генерирующий составную последовательность:

Ak=xor(x,y);

Результат работы:

Ak =

Columns 1 through 18

0 0 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0 0

Columns 19 through 36

1 1 0 1 0 1 0 1 1 1 0 0 0 1 0 1 0 0

Columns 37 through 54

1 0 1 0 1 1 0 1 1 1 1 0 1 0 0 0 0 0

Columns 55 through 63

1 1 0 0 1 1 0 0 0

График получившейся последовательности, представлен на рисунке 3.1.

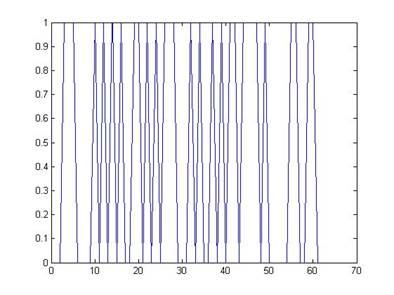
Рисунок 3.1 – График составной последовательности

3.2 Построение периодической АКФ составной последовательности.

Код, генерирующий составную последовательность:

l=length(Ak);

sk=[Ak Ak];

for k=0:l-1

A=sum(sk(k+1:l+k)==Ak(1:l));

D=sum(sk(k+1:l+k)~=Ak(1:l));

Rpakf(k+1)=(A-D)/l;

end

График периодической АКФ, представлен на рисунке 3.2.

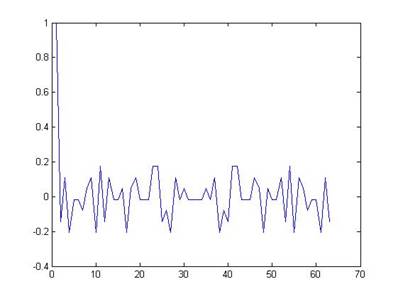
Рисунок 3.2 – График ПАКФ составной последовательности

Выводы:

1. Ознакомились с методами формирования и корреляционными свойствами широкополосных сигналов.

2. Псевдослучайная последовательность — последовательность чисел, которая была вычислена по некоторому определённому арифметическому правилу, но имеет все свойства случайной последовательности чисел в рамках решаемой задачи.

3. Ненормированная функция взаимной корреляции между двумя последовательностями одинаковой длины представляет собой совокупность величин корреляции одной последовательности со всеми циклическими перестановками другой. Автокорреляционная функция последовательности есть совокупность величин корреляции этой последовательности со всеми своими циклическими перестановками.

4. Функцию взаимной корреляции достаточно определить только для периода последовательности, так как в результате ее сдвига на эту величину она принимает свое исходное положение.

5. Так как функция взаимной корреляции получается в результате суммирования (или интегрирования) сигналов за их общий период, то она не зависит от положения их начала.