Работа на лопатках и мощность турбины
В результате взаимодействия газового потока с лопатками рабочего колеса возникает крутящий момент, являющийся конечной целью преобразования энергии в турбине.
Рассмотрим механизм действия сил и образования крутящего момента на примере одной рабочей лопатки, изображенной на рис. 3.4.
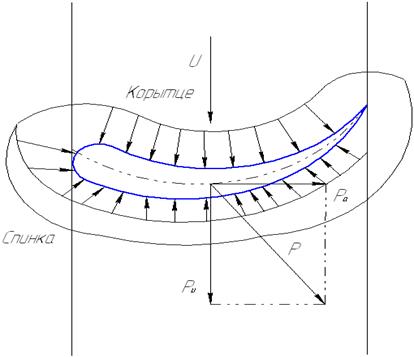
Рис. 3.4
Рабочая лопатка имеет несимметричный профиль; ее выпуклую сторону обычно называют спинкой, а вогнутую – корытцем.
При обтекании лопатки потоком газа на нее действуют силы давления и силы трения, причем силы давления распределяются по поверхности лопатки неравномерно: на вогнутую часть действуют большие давления, чем на спинку. Характер распределения давления по контуру рабочей лопатки в общем случае определяется ускорением потока газа в межлопаточном канале и воздействием на лопатку реактивной силы.
При повороте ускоряющегося потока частицы газа отбрасываются к корытцу лопатки, где создается повышенное давление. Следовательно, по ширине межлопаточного канала давление изменяется от максимального на корытце до минимального на спинке. Равнодействующую сил давления Р можно разложить на две составляющие: окружное усилие 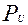 , действующее в направлении вращения ротора, и осевое усилие
, действующее в направлении вращения ротора, и осевое усилие 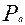 , действующее по оси вала турбины.
, действующее по оси вала турбины.
Крутящий момент на валу турбины создается окружным усилием 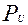 .
.
Для расчетного определения крутящего момента, работы и мощности турбины под 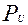 понимают суммарное окружное усилие на все лопатки, действующее на средней окружности рабочего колеса.
понимают суммарное окружное усилие на все лопатки, действующее на средней окружности рабочего колеса.
В соответствии с законом количества движения применительно к массе газа, протекающего через рабочее колесо за 1 сек.
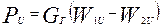
| (3.4) |
| где | 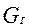 - расход газа, кг/с; - расход газа, кг/с;
|
 - проекции относительных скоростей - проекции относительных скоростей  на плоскость вращения рабочего колеса. на плоскость вращения рабочего колеса.
|
Из треугольников скоростей турбинной ступени (рис. 3.3) видно, что
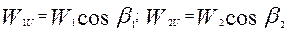
или
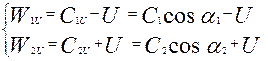
| (3.5) |
Таким образом из формулы 3.4 следует, что
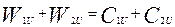
| (3.6) |
Направление силы 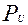 считается положительным, если оно совпадает с направлением вектора окружной скорости
считается положительным, если оно совпадает с направлением вектора окружной скорости 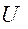 . Окружная составляющая относительной скорости
. Окружная составляющая относительной скорости 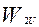 имеет отрицательный знак, т.к. она направлена в сторону, обратную направлению
имеет отрицательный знак, т.к. она направлена в сторону, обратную направлению 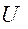 , поэтому при использовании формулы 3.4 перед
, поэтому при использовании формулы 3.4 перед 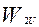 следует ставить знак плюс. Если же учитывать лишь величину скоростей, без учета их знака, формула 3.3 может быть записана в следующем виде:
следует ставить знак плюс. Если же учитывать лишь величину скоростей, без учета их знака, формула 3.3 может быть записана в следующем виде:
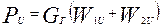
| (3.4а) |
С учетом зависимости 3.6
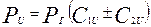
| (3.4б) |
В формуле 3.4б перед 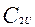 знак минус ставится, если
знак минус ставится, если 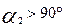 , а знак плюс, если
, а знак плюс, если 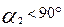 . (В надувочных газовых турбинах, как правило,
. (В надувочных газовых турбинах, как правило, 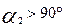 , следовательно, перед
, следовательно, перед 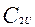 в этом случае следует ставить знак минус).
в этом случае следует ставить знак минус).
Работа на окружности колеса турбины, отнесенная к одному килограмму газа, равна произведению усилия 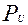 на окружную скорость
на окружную скорость 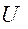 :
:
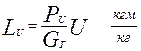
| (3.7) |
Окружную скорость можно выразить как произведение угловой скорости 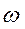 на средний радиус рабочего колеса
на средний радиус рабочего колеса 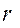 , т.е.
, т.е.
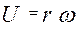
С учетом 3.6
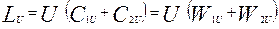
| (3.8) |
Величина крутящего момента на валу турбины может быть определена следующим образом:

Мощность турбины, выраженная в кВт при известной величине работы 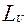 составит
составит
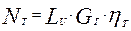 кВт кВт
| (3.9) |
Если известна окружная скорость 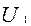 работа газа определяется величиной алгебраической разности (с учетом) проекций абсолютных скоростей
работа газа определяется величиной алгебраической разности (с учетом) проекций абсолютных скоростей 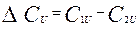 , которая зависит от изменения направления скорости газового потока и называется закруткой потока.
, которая зависит от изменения направления скорости газового потока и называется закруткой потока.
Из полученных выражений следует, что для определения работы и мощности турбины надо знать секундный расход газа 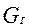 и величины векторов скоростей, т.е. треугольники скоростей ступени. Применительно к надувочной газовой турбине расход газа определяется как сумма расходов воздуха и топлива в дизеле
и величины векторов скоростей, т.е. треугольники скоростей ступени. Применительно к надувочной газовой турбине расход газа определяется как сумма расходов воздуха и топлива в дизеле
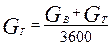 кг/с
кг/с
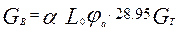 кг/час
кг/час
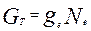
или
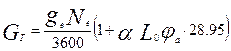 кг/с
кг/с
Дата добавления: 2015-07-24; просмотров: 3124;
