Анализ устойчивости по ЛЧХ

Оценку устойчивости по критерию Найквиста удобнее производить по ЛЧХ разомкнутой САУ. Очевидно, что каждой точке АФЧХ будут соответствовать определенные точки ЛАЧХ и ЛФЧХ.

Пусть известны частотные характеристики двух разомкнутых САУ (1 и 2), отличающихся друг от друга только коэффициентом передачи K₁ < K₂. Пусть первая САУ устойчива в замкнутом состоянии, вторая нет.(рис.79).

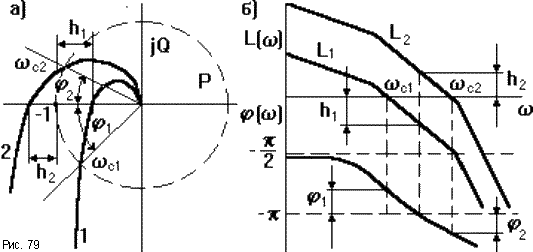
Если W₁(p) - передаточная функция первой САУ, то передаточная функция второй САУ W₂(p) = K 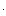W₁(p), где K = K₂/K₁. Вторую САУ можно представить последовательной цепочкой из двух звеньев с передаточными функциями K (безынерционное звено) и W₁(p), поэтому результирующие ЛЧХ строятся как сумма ЛЧХ каждого из звеньев.

Поэтому ЛАЧХ второй САУ: L₂( ) = 20lgK + L₁( ),

а ЛФЧХ: ₂( ) = ₁( ).

Пересечениям АФЧХ вещественной оси соответствует значение фазы = - . Это соответствует точке пересечения ЛФЧХ = - линии координатной сетки. При этом, как видно на АФЧХ, амплитуды A₁( ) < 1, A₂( ) > 1, что соответствует на САЧХ значениям L₁( ) = 20lgA₁( ) < 0 и L₂( ) > 0.

Сравнивая АФЧХ и ЛФЧХ можно заключить, что система в замкнутом состоянии будет устойчива, если значению ЛФЧХ = - будут соответствовать отрицательные значения ЛАЧХ и наоборот. Запасам устойчивости по модулю h₁ и h₂, определенным по АФЧХ соответствуют расстояния от оси абсцисс до ЛАЧХ в точках, где = - , но в логарифмическом масштабе.

Особыми точками являются точки пересечения АФЧХ с единичной окружностью. Частоты _c1 и _c2, при которых это происходит называют частотами среза.

В точках пересечения A( ) = 1 = > L( ) = 0 - ЛАЧХ пересекает горизонтальную ось. Если при частоте среза фаза АФЧХ _c1 >- (рис.79а кривая 1), то замкнутая САУ устойчива. На рис.79б это выглядит так, что пересечению ЛАЧХ горизонтальной оси соответствует точка ЛФЧХ, расположенная выше линии = - . И наоборот для неустойчивой замкнутой САУ (рис.79а кривая 2) _c2 < - , поэтому при = _c2 ЛФЧХ проходит ниже линии = - . Угол ₁ = _c1-(- ) является запасом устойчивости по фазе. Этот угол соответствует расстоянию от линии = - до ЛФЧХ.

Исходя из сказанного, критерий устойчивости Наквиста по логарифмическим ЧХ, в случаях, когда АФЧХ только один раз пересекает отрезок вещественной оси [- 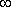;-1], можно сформулировать так: для того, чтобы замкнутая САУ была устойчива необходимо и достаточно, чтобы частота, при которой ЛФЧХ пересекает линию = - , была больше частоты среза.

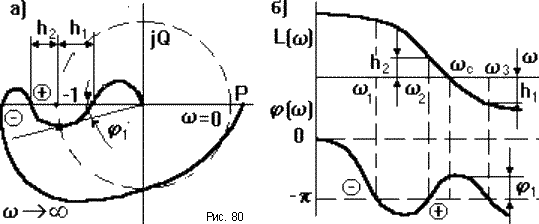
Если АФЧХ разомкнутой САУ имеет сложный вид (рис.80), то ЛФЧХ может несколько раз пересекать линию = - . В этом случае применение критерия Найквиста несколько усложняется. Однако во многих случаях данной формулировки критерия Найквиста оказывается достаточно.

Лекция 11. Качество САУ