Элементарные динамические звенья. Динамика большинства функциональных элементов САУ независимо от исполнения может быть описана одинаковыми по форме дифференциальными уравнениями не более

Динамика большинства функциональных элементов САУ независимо от исполнения может быть описана одинаковыми по форме дифференциальными уравнениями не более второго порядка. Такие элементы называют элементарными динамическими звеньями. Передаточная функция элементарного звена в общем виде задается отношением двух полиномов не более чем второй степени:

W_э(p) = .

Известно также, что любой полином произвольного порядка можно разложить на простые сомножители не более, чем второго порядка. Так по теореме Виета модно записать

D(p) = a_opⁿ + a₁p^{n - 1} + a₂p^{n - 2} + ... + a_n = a_o(p - p₁)(p - p₂)...(p - p_n),

где p₁, p2, ..., p_n - корни полинома D(p). Аналогично

K(p) = b_opm + b₁p^{m - 1}+ ... + bm = b_o(p - p^~₁)(p - p^~₂)...(p - p^~m),

где p^~₁, p^~₂, ..., p^~m - корни полинома K(p). То есть

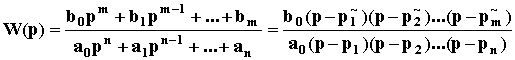
Корни любого полинома могут быть либо вещественными p_i = a_i, либо комплексными попарно сопряженными p_i = a_i ± j _i . Любому вещественному корню при разложении полинома соответствует сомножитель (p - a_i ). Любая пара комплексно сопряженных корней соответствует полиному второй степени, так как

(p - a_i + j _i )(p - a_i - j _i ) = (p - ai)² + _i ² = p² - 2pa_i + (a_i ² + _i ²).

То есть

Поэтому любую сложную передаточную функцию линеаризованной САУ можно представить как произведение передаточных функций элементарных звеньев. Каждому такому звену в реальной САУ, как правило, соответствует какой - то отдельный узел. Зная свойства отдельных звеньев можно судить о динамики САУ в целом.

В теории удобно ограничиться рассмотрением типовых звеньев, передаточные функции которых имеют числитель или знаменатель, равный единице, то есть

W(p) = 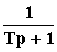, W(p) = ,

W(p) = 1/p, W(p) = p, W(p) = Tp + 1, W(p) = k.

Из них могут быть образованы все остальные звенья. Звенья, у которых порядок полинома числителя больше порядка полинома знаменателя, технически нереализуемы.

Лекция 4.Структурные схемы САУ