Сила тяжести

Так как сила тяготения и сила инерции неотличимы, то при использовании неинерциальной системы их обычно складывают (как вектора) и эту сумму называют силой тяжести.

Силой тяжести, действующей на тело в неинерциальной системе отсчета, называется сумма силы тяготения и силы инерции:

F _тяж = F _тяг +F _и (8.2)

В рассмотренном выше примере со стартующим кораблем (рис. 8.1) сила тяжести равна:

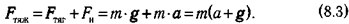
Сила тяжести сообщает всем телам одинаковое ускорение (относительно данной системы), которое называют местным ускорением свободного падения 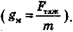В примере со стартующим кораблем

g_m=a+g.

Обратим внимание на то, что сила тяжести зависит от того, какой системой отсчета мы пользуемся. Так, например, в рассматриваемом случае можно поступить одним из двух способов.

1. Выбрать систему, связанную с Землей. В этой системе тело движется с ускорением под действием силы натяжения нити (Т) и силы тяжести (mg). Уравнение движения:

Т - mg = та.

2. Выбрать систему, связанную с кораблем. В этой системе тело находится в состоянии покоя под действием силы натяжения нити (Т) и местной силы тяжести (mg + та). Уравнение покоя:

T = mg+ma.

Очевидно, что эти уравнения одинаковы.

Для человека, находящегося в корабле, естественным является второй способ. Поэтому он скажет, что при старте сила тяжести возрастает.

С направлением силы тяжести неразрывно связаны такие понятия, как вертикаль и горизонталь.

Вертикалью называется линия, вдоль которой направлена сила тяжести.

Горизонтальной плоскостью называется плоскость, которая перпендикулярна силе тяжести.

Формула (8.2) определяет силу тяжести в любой неинерциальной системе отсчета. Применим ее к Земле, неинерциальность которой связана с вращением вокруг своей оси. Вследствие этого точки земной поверхности обладают центростремительным ускорением (а_ц), которое и является ускорением неинерциальной системы (а_с = а_ц). По формуле (8.2) находим силу инерции:

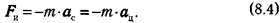
Знак «—» указывает на то, что сила инерции направлена от оси вращения Земли.

Сила тяготения направлена к центру Земли. Складывая эти силы, находим силу тяжести (рис. 8.2).

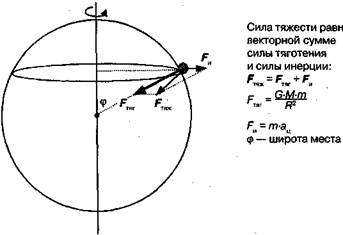
Рис. 8.2.Сила тяготения и сила тяжести

На рис. 8.2 видно отличие силы тяжести от силы тяготения. Наибольшей величины это отличие достигает на экваторе, где сила тяготения и сила инерции направлены по одной прямой в противоположные стороны. При сложении таких векторов (8.2) их величины вычитаются:

Таким образом, сила тяжести отличается от силы тяготения на величину силы инерции. Велико ли это отличие? Для ответа на этот вопрос найдем отношение силы инерции к силе тяжести. Сила тяжести создает ускорение свободного падения: Р_гяж = m-g (g = 9,8 м/с²). Сила инерции вычисляется по формуле (8.3) F = т-а , деля величины этих сил, найдем

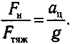(8.6)

Центростремительное ускорение рассчитывается по формуле (3.9):

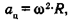
где R — радиус обращения тела, а 0) — угловая скорость вращения Земли. Для экватора R = 6 400 000 м — радиус Земли. Угловая скорость выражается через период обращения (Т), который для Земли составляет 1 сутки или 86400 с. В соответствии с формулой (3.10) ω= 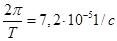. Центростремительное ускорение на экваторе а_ц= ω ²R 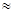0,03 м/с². Подставив это значение в (8.5) получим

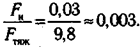
Из приведенных расчетов видно, что для Земли сила инерции составляет всего 0,3% от силы тяжести. Поэтому в большинстве случаев неинерциальностью Земли можно пренебречь.