Простейшие механизмы. На использовании законов статики основано действие простейших механизмов, используемых для изменения величины или направления силы.

На использовании законов статики основано действие простейших механизмов, используемых для изменения величины или направления силы.

Рычаг — твердое тело чаще в виде стержня, которое может вращаться (поворачиваться) вокруг неподвижной оси.

Пусть ось делит рычаг в отношении L₁:L₂ и на него действуют две параллельные силы F₁ и F₂ (рис. 7.13). Будем также считать, что силой тяжести, действующей на рычаг, можно пренебречь.

Определим положение оси вращения (О), при котором рычаг будет оставаться в равновесии.

Рис. 7.13.Равновесие рычагов 1-го (а) и 2-го (б) рода

По правилу моментов (7.8) М₁ + М₂ = 0 →— F₁∙L₁ + F₂∙L₂ = 0 или

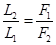
При равновесии рычага под действием двух параллельных сил ось вращения делит расстояние между точками приложения сил на отрезки обратно пропорциональные величинам сил.

Равновесие рычага наступает при условии, что отношение приложенных к его концам параллельных сил обратно отношению плеч и моменты этих сил противоположны по знаку. Поэтому, прикладывая небольшую силу к длинному концу рычага, можно уравновесить гораздо большую силу, приложенную к короткому концу рычага. В зависимости от взаимного расположения точек приложения сил и оси различают рычаги 1-го и 2-го рода (рис. 7.13):

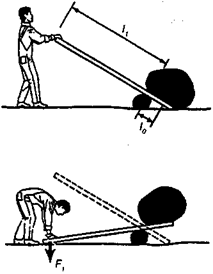
Рис. 7.14.Использование шеста в качестве рычага 1-го рода

а) Рычаг 1-го рода. Силы расположены по обе стороны от оси. Подобными рычагами являются длинный шест, с помощью которого поднимают тяжелый камень (рис. 7.14.).

б) Рычаг 2-го рода. Силы расположены по одну сторону от опоры. К данному виду относится, например, тачка (рис. 7.15), при использовании которой усилие рук приложено на «максимальном» расстоянии от оси колеса (максимальное плечо), что позволяет перевозить большие грузы.

Рис. 7.15.Тачка — рычаг 2-го рода

Применение рычага в механизмах дает выигрыш в силе, при этом столько же проигрывается в перемещении. Рычаг не дает выигрыша в работе.

Многие суставы работают по принципу рычага второго рода. При этом мышцы, действуют на меньшее плечо рычага, рис. 7.16. Это приводит к проигрышу в силе, и к выигрышу в перемещении и скорости. В результате, при сравнительно малом по протяженности движении мышцы, звено или конечность описывают значительно большую траекторию.

Эта особенность в строении костно-мышечных узлов должна вызвать дополнительные осложнения в центральном регулировании движений, так как увеличение траектории перемещения звеньев сочетается с большим количеством степеней свободы подвижности, присущих человеческому телу как кинематической цепи.

Балансир (фр. balancier — коромысло) — двуплечный рычаг, совершающий качательные (колебательные) движения около неподвижной оси. Применяется в балансирующем маятнике, использующемся в механотерапии.

Блок, как и рычаг, относится к простейшим механизмам, рис. 7.17. Он выполняется в форме диска, свободно вращающегося на оси. По окружности диск имеет желоб для цепи (каната, нити). Используется равенство натяжения во всех точках цепи, которая движется без трения.

Неподвижный блок (рис. 7.17, а) не дает выигрыша в силе, но позволяет изменять ее направление. Так, можно поднимать груз вверх, действуя на веревку силой, направленной вниз, что менее утомительно: F = P.

Подвижный блок (рис. 7.17, б) дает двукратный выигрыш в силе:

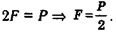
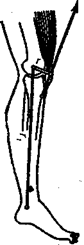
Рис. 7.16.Схема действия мышцы, разгибающей ногу в коленном суставе: плечо r действия мышцы существенно короче плеча r_1,стрелкой отмечено направление мышечной тяги

Для удобства применения подвижный блок часто используют в комбинации с неподвижным (рис. 7.17, в).

Аппараты блокового типа применяются в механотерапии при тренировках по облегчению (восстановлению) движений в суставах и укреплению мышц.

К простейшим механизмам относится и наклонная плоскость. При описании положения тела в этом случае используют прямоугольную систему координат, ось ОХ которой направлена параллельно плоскости, а ось ОУ — перпендикулярно ей. На тело, расположенное на наклонной плоскости, рис. 7.18, действуют сила тяжести mg, сила реакции опоры — N и сила трения F_тр . Проекции сила тяжести на координатные оси равны mg·sinα (скатывающая сила) и mg·cosα.

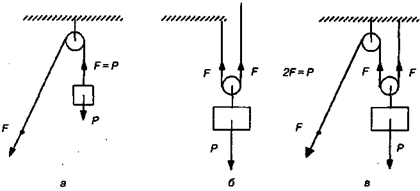
Рис. 7.17.Блоки: а) неподвижный, б) подвижный, в) комбинация

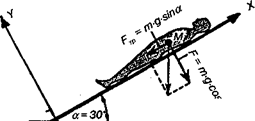
Рис. 7.18.Силы, действующие на тело человека, находящегося на наклонной поверхности

Условия равновесия определяются следующими соотношениями:

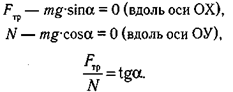
При движении вниз по наклонной плоскости скатывающая сила помогает движению и способствует значительному увеличению скорости. При заданной длине наклонной плоскости скатывающая сила прямо пропорциональна высоте, рис. 7.19.

Наклонная поверхность часто используется на тренировках при выполнении различных упражнений, рис. 7.20.

При восстановлении после травм эффективны занятия на специальном столе, конструкция которого позволяет изменять угол наклона его плоскости к горизонту, рис. 7.21.

Изменение угла наклона и места крепления фиксирующих ремней (на уровне крупных суставов ног, поясничного и грудного отделов позвоночника) позволяет дозировать нагрузку на опорно-двигательную, сердечно-сосудистую и вестибулярную системы.

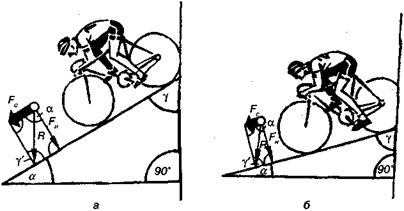
Рис. 7.19.Движение велосипедиста с наклонной плоскости: а) большая высота, б) малая высота

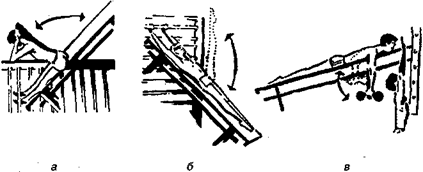
Рис. 7.20.Упражнения на наклонной плоскости:

а) выпрямление туловища, б) поднимание ног,

в) упражнения для рук с гантелями

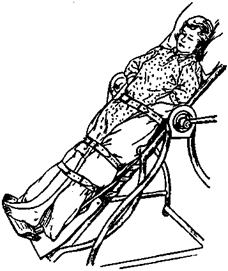
Рис.7.21. Тренировка ортостатических функций на специальном наклонном поворотном столе