Метод корреляций
Не со всеми проблемами можно справиться экспериментальным методом. Существует множество ситуаций, когда исследователь не может контролировать, какие испытуемые попадают в те или иные условия. Например, если надо проверить гипотезу, что люди с анорексией более чувствительны к изменениям вкуса, чем люди с нормальным весом, то не можем же мы собрать группу испытуемых с нормальным весом и потребовать, чтобы у половины из них появилась анорексия! На самом деле нам придется отобрать людей, уже страдающих анорексией, и тех, у кого вес в норме, и проверить, различаются ли они также по вкусовой чувствительности. Вообще говоря, можно использовать метод корреляций, чтобы определить связана ли некоторая переменная, которую мы не можем контролировать, с другой интересующей нас переменной, или, иначе говоря, коррелируют ли они между собой.
В вышеприведенном примере у переменной веса есть только два значения — нормальный и анорексичный. Чаще случается, что каждая из переменных может принимать много значений, и тогда надо определить, насколько величины одной и другой переменной коррелируют между собой. Определить это может статистический параметр, называемый коэффициентом корреляции и обозначаемый буквой r. Коэффициент корреляции позволяет оценить, насколько связаны две переменные, и выражается числом от -1 до +1. Ноль означает отсутствие связи; полная связь выражается единицей (+1, если отношение положительное, и -1, если оно отрицательное). По мере увеличения r от 0 до 1 сила связи возрастает.
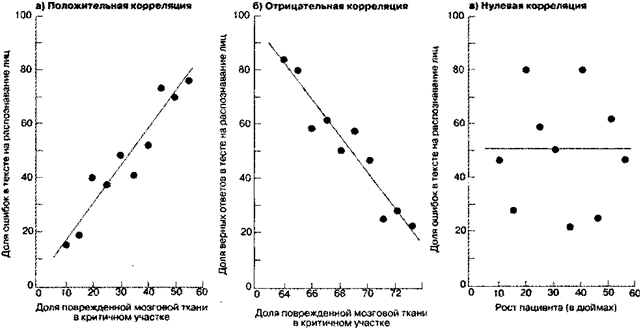
Рис. 1.6. Графики рассеивания, иллюстрирующие корреляцию.Эти гипотетические данные принадлежат 10 пациентам, каждый из которых имеет некоторое повреждение участков мозга, ответственных, насколько известно, за узнавание лиц. На рис. 1.6а пациенты располагаются вдоль горизонтали соответственно объему повреждения мозга, причем самая левая точка показывает пациента с наименьшим повреждением (10%), а самая правая точка показывает пациента с наибольшим повреждением (55%). Каждая точка на графике отражает показатель для отдельного пациента в тесте на узнавание лиц. Корреляция положительная и равна 0,90. На рис. 1.6б изображены те же самые данные, но теперь они показывают долю правильных ответов, а не ошибок. Здесь корреляция отрицательная, равная -0,90. На рис. 1.6в успехи пациентов в тесте на распознавание отображены в зависимости от их роста. Здесь корреляция равна нулю.
Суть коэффициента корреляции можно пояснить на примере графического представления данных гипотетического исследования. Как показано на рис. 1.6а, в исследовании участвуют пациенты, о которых заранее известно, что у них поврежден мозг, и это вызвало разной степени трудности в узнавании лиц (прозопагнозия). Предстоит выяснить, возрастает ли трудность, или ошибка узнавания лиц, с увеличением процента поврежденной мозговой ткани. Каждая точка на графике 1.6а показывает результат для отдельного пациента при его тестировании на узнавание лиц. Например, пациент с 10%-ным повреждением ошибался в тесте на распознавание лиц в 15% случаев, а пациент с 55%-ным повреждением делал ошибки в 95% случаев. Если бы ошибка узнавания лиц постоянно возрастала с увеличением процента повреждения мозга, точки на графике располагались бы все время выше при движении слева направо; если бы они размещались на диагонали рисунка, коэффициент корреляции был бы r = 1,0. Однако несколько точек расположены по разные стороны этой линии, поэтому корреляция составляет около 90%. Корреляция 90% означает очень сильную связь между объемом поврежденного мозга и ошибками узнавания лиц. Корреляция на рис. 1.6а — положительная, поскольку большее повреждение мозга вызывает больше ошибок.
Если бы вместо ошибок мы решили отобразить долю правильных ответов в тесте на распознавание, то получили бы график, изображенный на рис. 1.6б. Здесь корреляция отрицательная (равная примерно -0,90), поскольку с увеличением повреждения мозга доля правильных ответов уменьшается. Диагональ на рис. 1.6б — это просто инверсный вариант той, что на предыдущем рисунке.
Наконец, обратимся к графику на рис. 1.6в. Здесь отображена доля ошибок пациентов в тесте на распознавание лиц в зависимости от их роста. Разумеется, нет оснований считать, что доля узнанных лиц связана с ростом пациента, и график подтверждает это. При движении слева направо точки не проявляют согласованного движения ни вниз, ни вверх, а разбросаны вокруг горизонтальной линии. Корреляция равна нулю.
Числовой метод вычисления коэффициента корреляции описан в Приложении II. Сейчас, однако, мы сформулируем несколько элементарных правил, которые помогут вам разобраться с коэффициентом корреляции, когда вы встретитесь с ним в последующих главах.
Корреляция бывает положительной (+) и отрицательной (-). Знак корреляции показывает, связаны ли две переменные положительной корреляцией (величина обеих переменных растет или уменьшается одновременно) или отрицательной корреляцией (одна переменная растет при уменьшении другой). Предположим, например, что количество пропусков занятий студентом имеет корреляцию -0,40 с баллами в конце семестра (чем больше пропусков, тем меньше баллов). С другой стороны, корреляция между полученными баллами и количеством посещенных занятий будет +0,40. Прочность связи одна и та же, но знак ее зависит от того, считаем ли мы пропущенные или посещенные занятия.
По мере усиления связи двух переменных r увеличивается от 0 до 1. Чтобы лучше это представить, рассмотрим несколько известных положительных коэффициентов корреляции:
- Коэффициент корреляции между баллами, полученными в первый год обучения в колледже, и баллами, полученными на втором году, составляет около 0,75.
- Корреляция между показателями геста на интеллект в возрасте 7 лет и при повторном тестировании в 18 лет составляет примерно 0,70.
- Корреляция между ростом одного из родителей и ростом ребенка во взрослом возрасте, составляет около 0,50.
- Корреляция между результатами теста на способность к обучению, полученными в школе и в колледже, равна примерно 0,40.
- Корреляция между баллами, полученными индивидуумами в бланковых тестах, и суждением психолога-эксперта об их личностных качествах составляет около 0,25.
В психологических исследованиях коэффициент корреляции 0,60 и выше считается достаточно высоким. Корреляция в диапазоне от 0,20 до 0,60 имеет практическую и теоретическую ценность и полезна при выдвижении предсказаний. К корреляции от 0 до 0,20 следует относиться осторожно, при выдвижении предсказаний ее польза минимальна.
Тесты.Знакомый пример использования корреляционного метода — тесты по измерению некоторых способностей, достижений и других психологических качеств. При тестировании группе людей, различающихся по какому-нибудь качеству (например, математическим способностям, ловкости рук или агрессивности), предъявляют некоторую стандартную ситуацию. Затем можно вычислить корреляцию между изменениями показателей данного теста и изменением другой переменной. Например, можно установить корреляцию между показателями группы студентов в тесте на математические способности и их оценками по математике при дальнейшем обучении в колледже; если корреляция значительная, то на основе результатов этого теста можно решить, кого из нового набора студентов можно перевести в группу с повышенными требованиями.
Тестирование— важный инструмент психологических исследований. Оно позволяет психологам получать большое количество данных о людях с минимальным отрывом их от повседневных дел и без применения сложного лабораторного оборудования. Построение тестов включает множество этапов, которые мы подробно рассмотрим в последующих главах.
Корреляция и причинно-следственные связи.Между экспериментальными и корреляционными исследованиями есть важное различие. Как правило, в экспериментальном исследовании систематически манипулируют одной переменной (независимой) с целью определить ее причинное воздействие на некоторые другие переменные (зависимые). Такие причинно-следственные связи нельзя вывести из корреляционных исследований. Ошибочное понимание корреляции как причинно-следственного отношения можно проиллюстрировать на следующих примерах. Может существовать корреляция между мягкостью асфальта на улицах города и количеством солнечных ударов, случившихся за день, но отсюда не следует, что размягченный асфальт выделяет какой-то яд, приводящий людей на больничную койку. На самом деле изменение обеих этих переменных — мягкости асфальта и числа солнечных ударов — вызывается третьим фактором — солнечным теплом. Еще один простой пример — высокая положительная корреляция между большим количеством аистов, гнездящихся во французских деревнях, и высокой рождаемостью, зарегистрированной там же. Предоставим изобретательным читателям самим догадываться о возможных причинах такой корреляции, не прибегая к постулированию причинно-следственной связи между аистами и младенцами. Эти примеры служат достаточным предостережением от понимания корреляции как причинно-следственного отношения. Если между двумя переменными есть корреляция, изменение одной может вызывать изменения другой, но без специальных экспериментов такой вывод будет неоправданным.
Дата добавления: 2015-07-22; просмотров: 861;
