Тверді тіла
Структура твердого тіла 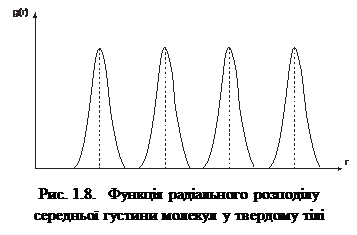 .На відміну від газоподібного і рідкого стану, речовини у твердому стані мають властивість зберігати густину й об’єм. У твердому тілі сили міжмолекулярної взаємодії настільки значні, що тепловий рух молекул практично не впливає на формування їхньої структури. У твердих тілах потенціальна енергія міжмолекулярної взаємодії значно більша від кінетичної енергії теплового руху (/Еп/>>kТ). За цих умов моле-кули твердого тіла розміщені у фіксованих положеннях, які відповідають стану стійкої рівноваги, коли Fв=Fпр, а Еп=Еп.min(див. рис.1.1).
.На відміну від газоподібного і рідкого стану, речовини у твердому стані мають властивість зберігати густину й об’єм. У твердому тілі сили міжмолекулярної взаємодії настільки значні, що тепловий рух молекул практично не впливає на формування їхньої структури. У твердих тілах потенціальна енергія міжмолекулярної взаємодії значно більша від кінетичної енергії теплового руху (/Еп/>>kТ). За цих умов моле-кули твердого тіла розміщені у фіксованих положеннях, які відповідають стану стійкої рівноваги, коли Fв=Fпр, а Еп=Еп.min(див. рис.1.1).
Очевидно, що умови рівноважного розташування молекул у твердому тілі поширюються на весь його об’єм і спричинюють виникнення просторової періодичної структури. Ця періодична структура має вигляд кристалічної ґратки. У кристалічній ґратці молекули (атоми, іони) розміщені у її вузлах –
точках, що відповідають положенню рівноваги. Характер руху молекул твердого тіла коливальний. Тверді тіла мають просторову структуру, для якої, на відміну від речовини, характерний як ближній, так і дальній порядок. Експериментальним підтвердженням кристалічної структури твердих тіл є результати рентгеноструктурного дослідження їхньої функції радіального розподілу g(r), показані на рис. 1.8. Як бачимо, просторова впорядкованість молекул, що утворюють кристалічну ґратку, є головною ознакою твердих тіл.
Зазначимо, що всі тверді тіла можна розділити на два типи – монокристалічні та полікристалічні. У монокристалах дальній порядок чітко витриманий у всьому об’ємі твердого тіла. Природні монокристали (гірський кришталь, сапфір, алмаз тощо) мають, здебільшого, правильну форму багатогранника і є анізотропними, тобто їхні фізичні властивості різні, залежно від напряму вимірювання. Полікристалічні тіла складаються з великої кількості дрібних монокристалів, розміри і просторова орієнтація яких є різними. Завдяки такій будові полікристалічні зразки ізотропні.
У розмаїтті речовин навколишнього світу є й такі, що поєднують властивості рідин і твердих тіл. Це так звані аморфні тіла (скло, бурштин, пластики та ін.), які, зазвичай, ми зачислюємо до твердих. За окремими властивостями вони справді мають ознаки твердого тіла (здатність зберігати форму й об’єм, механічну стійкість до деформацій, перехід у рідкий стан під час нагрівання та ін.). Водночас за структурою вони ближчі до рідин. Зокрема, для аморфних тіл характерний лише ближній порядок у розміщенні атомів. У них зовсім нема кристалічної структури. Саме тому аморфні тіла слід розглядати як переохолоджені рідини, що перебувають у метастабіль-ному (нестійкому) стані.
Надалі під поняттям тверде тіло ми розумітимемо лише кристалічні речовини.
Кристалічна ґратка.У будь-якому кристалі елементарні структурні частинки (атоми, молекули, іони) розміщені періодично вздовж будь-якого напряму, утворюючи кристалічну ґратку (рис. 1.9).
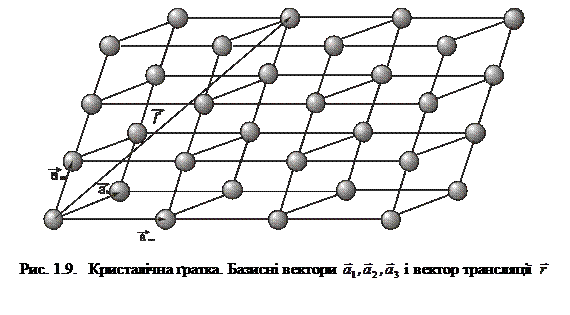 |
Якщо координатні осі XYZ вибрати так, щоб вони збігались із ребрами кристала, то вздовж кожного з цих ребер атоми будуть розміщені на однакових відстанях а1, а2, а3, відповідно. Ці відстані називають основними періодами ґратки, а паралелепіпед з ребрами а1, а2, а3 та разом з атомами в його вершинах – елементарною коміркою кристалічної ґратки. Вектори
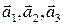 називають базисними. За допомогою базисних векторів можна записати радіус-вектор
називають базисними. За допомогою базисних векторів можна записати радіус-вектор 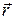 , який визначає положення будь-якого атома в кристалічній ґратці:
, який визначає положення будь-якого атома в кристалічній ґратці:
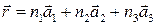 , (1.14)
, (1.14)
де n1, n2, n3 – натуральні числа. Вектор 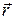 називають вектором трансляції.
називають вектором трансляції.
Кристалічну ґратку, яка задовольняє умову (1.14), називають примітивною ґраткою, а її елементарну комірку – примітивною коміркою.
Зазначимо, що складні кристалічні ґратки складаються з кількох примітивних.
Симетрія кристалів. Елементи симетрії.Закономірно, що просторова періодичність у розміщенні атомів кристала та його частин
зумовлює симетрію кристала. Надалі під поняттям симетрії розумітимемо здатність твердого тіла суміщатись із собою під час його рухів або певних операцій над його точками. До елементів симетрії твердих тіл належать:
1) площина симетрії Р;
2) поворотна вісь симетрії n-го порядку Ln;
3) центр симетрії, або центр інверсії С;
4) дзеркально-поворотна вісь симетрії n-го порядку 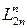 ;
;
5) вісь інверсії Lin.
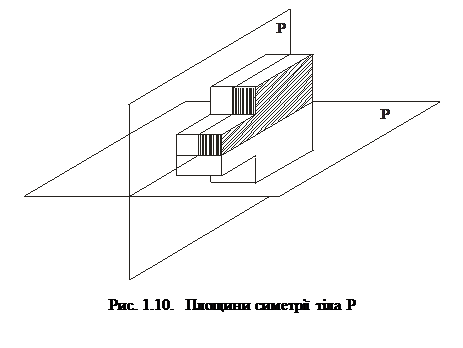 |
Якщо тіло суміщається собою в разі дзеркального відображення у заданій площині, то цю площину називають площиною симетрії Р (рис. 1.10).
Віссю симетрії n-го порядку Ln називають вісь, під час повертання навколо якої на кут 2p/n тіло суміщається з собою.
Якщо тіло можна сумістити з собою шляхом інверсії відносно точки С, то цю точку називають центром симетрії. Центр симетрії – це точка перетину трьох взаємо перпендикулярних площин симетрії тіла.
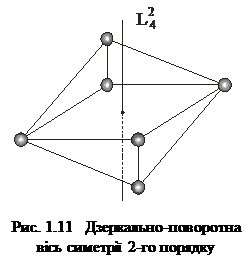
Дзеркально-поворотна вісь симетрії n-го порядку 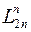 діє як сукупність осі симетрії n-го порядку і площини симетрії, що перпендикулярна до неї (рис.1.11).
діє як сукупність осі симетрії n-го порядку і площини симетрії, що перпендикулярна до неї (рис.1.11).
 Вісь інверсії n-го порядку Lіn діє як сукупність осі симетрії n-го порядку і центра інверсії С. Зазначимо, що Li1=C, a Li2=P. Загалом, як самостійні елементи симетрії існують лише Li4 і Li6. У разі описування структури кристалів треба мати на увазі, що не всі елементи симетрії існують у реальних кристалічних ґратках. Зокрема, доведено, що ґратчаста будова кристалів не допускає існування у кристалах осей симетрії іншого порядку, крім 1, 2, 3, 4, 5 і 6. Для позначення точкових елементів симетрії, характерних для просторової кристалічної ґратки, використовують і міжнародні позначення
Вісь інверсії n-го порядку Lіn діє як сукупність осі симетрії n-го порядку і центра інверсії С. Зазначимо, що Li1=C, a Li2=P. Загалом, як самостійні елементи симетрії існують лише Li4 і Li6. У разі описування структури кристалів треба мати на увазі, що не всі елементи симетрії існують у реальних кристалічних ґратках. Зокрема, доведено, що ґратчаста будова кристалів не допускає існування у кристалах осей симетрії іншого порядку, крім 1, 2, 3, 4, 5 і 6. Для позначення точкових елементів симетрії, характерних для просторової кристалічної ґратки, використовують і міжнародні позначення
L1=1; C=1;
L2=2; Li2=3;
L3=3; Li4=4;
L4=4; Li4=6;
L6=6; p = m.
П’ять описаних вище елементів симетрії кристалів називають точковими, оскільки їхня дія завжди залишає нерухомою хоча б одну точку кристала. Крім точкових елементів симетрії, для складних кристалів характерні ще й два просторові елементи симетрії – гвинтова вісь n-го порядку та площина дзеркального ковзання. Гвинтова вісь симетрії n-го порядку – це та вісь, переміщенням уздовж якої з одночасним повертанням на кут 2p/n кристалічну ґратку буде суміщено саму з собою. Площина дзеркального ковзання забезпечує таке суміщення кристалічної ґратки шляхом одночасного дзеркального відображення у площині та зсуву на певну відстань паралельно до площини.
Отже, поряд з елементами точкової симетрії кристалічна ґратка має трансляційну симетрію і просторові елементи симетрії. Сукупність усіх елементів симетрії ґратки називають її просторовою групою. Кристалограф Е. Федоров довів, що всього є 230 просторових груп симетрії кристалів.
У кристалографії сукупність елементів симетрії, притаманних конкретному кристалу, визначає його клас симетрії. У 1869 р. А. Гадолін, використовуючи закономірності складання елементів симетрії, довів, що в природі існує 32 класи симетрії кристалів. За параметрами елементарної комірки кристали поділяють на сім типів кристалографічних систем (сингоній). До однієї сингонії належать кристали з подібними елементарними комірками. У таких комірках співвідношення між довжинами векторів і відповідними кутами між ними однакові.
Ознаки кристалографічних систем (сингоній)
| Тип сингонії | Параметри елементарної комірки | |
| Кубічна | а1=а2=а3 | a=b=g=90° |
| Гексагональна | а1=а2¹а3 | a=b=90°, g=120° |
| Тетрагональна | а1=а2¹а3 | a=b=g=90° |
| Тригональна | а1=а2=а3 | a=b=g¹90° |
| Ромбічна | а1¹а2¹а3 | a=b=g=90° |
| Моноклінна | а1¹а2¹а3 | a=g=90°, g¹90° |
| Триклінна | а1¹а2¹а3 | a¹b¹g¹90° |
Ґратки Браве. Кристалографічні індекси.Автором сучасної теорії гратчастої будови кристалів є А. Браве, який 1855 р. математично довів існування 14 типів кристалічних ґраток. Учений виявив, що будь-яку просторову кристалічну ґратку можна відтворити шляхом трансляції одного паралелепіпеда вздовж кристалографічних напрямів. Такий елементарний паралелепіпед просторової ґратки називають ґраткою Браве. Чотирнадцять ґраток Браве розділені між сімома сингоніями так:
| Сингонія | Примі-тивна | Базо- центрована | Об’ємо- центрована | Гране- центрована |
| Триклінна | 
| |||
| Моноклінна | 
| 
| ||
| Ромбічна | 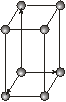
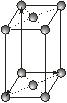
| 
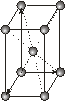
| 
| 
|
| Тригональна (ромбоедрична) | 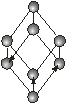
| |||
| Тетрагональна | 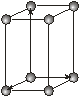
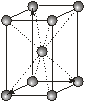
| 
| ||
| Гексагональна | 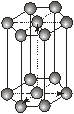
| |||
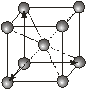
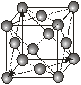
| Кубічна | 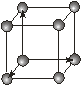
| 
| 
|
Кожна із семи сингоній має примітивну ґратку Браве. Базоцентровані ґратки є лише у моноклінній та ромбічній сингоніях, а гранецентровані – у ромбічній та кубічній. Об’ємоцентровані ґратки мають три сингонії – ромбічну, тетрагональну і кубічну.
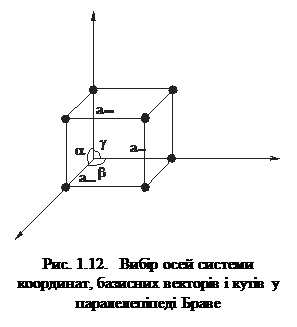 Положення атомів у кристалічній ґратці виражають за допомогою прямокутних або косокутних систем координат, осі яких збігаються з ребрами паралелепіпеда Браве, а початок координат міститься в одному із вузлів ґратки (рис.1.12). За масштабні одиниці осей координат вибирають довжини базисних векторів.
Положення атомів у кристалічній ґратці виражають за допомогою прямокутних або косокутних систем координат, осі яких збігаються з ребрами паралелепіпеда Браве, а початок координат міститься в одному із вузлів ґратки (рис.1.12). За масштабні одиниці осей координат вибирають довжини базисних векторів.
Для характеристики паралельних атомних площин у кристалі достатньо виразити одну з них. Рівняння будь-якої площини в прямокутних (або косокутних) координатах має вигляд
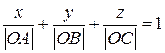 , (1.15)
, (1.15)
де ОА, ОВ і ОС – довжини відрізків (в одиницях масштабу), які площина відтинає на відповідних осях координат. Оскільки довжини цих відрізків є раціональними числами, то рівняння (1.15) можна записати у вигляді
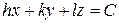 , (1.16)
, (1.16)
 де h, k, l – цілі числа, які не мають спільного множника. Ці числа однозначно визначають положення площини у просторі, їх називають індексами Міллера. У кристалографії індексами Міллера позначають атомні площини, записуючи їх у круглих дужках – (hkl). Якщо якийсь індекс є від’ємним, то його позначають знаком мінус зверху – (
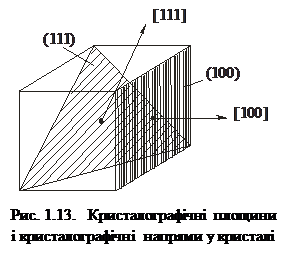
де h, k, l – цілі числа, які не мають спільного множника. Ці числа однозначно визначають положення площини у просторі, їх називають індексами Міллера. У кристалографії індексами Міллера позначають атомні площини, записуючи їх у круглих дужках – (hkl). Якщо якийсь індекс є від’ємним, то його позначають знаком мінус зверху – ( 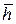 kl). Напрям у кристалі, перпендикулярний до заданої атомної площини, позначають тими ж індексами Міллера, записаними у квадратних дужках – [hkl]. На рис. 1.13 показані, як приклад, дві атомні площини і відповідні їм напрями у кристалі кубічної сингонії.
kl). Напрям у кристалі, перпендикулярний до заданої атомної площини, позначають тими ж індексами Міллера, записаними у квадратних дужках – [hkl]. На рис. 1.13 показані, як приклад, дві атомні площини і відповідні їм напрями у кристалі кубічної сингонії.
Дефекти кристалічної ґратки.
 |
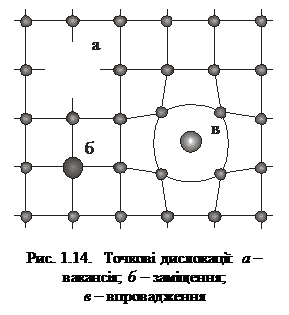 Дефектом кристалічної ґратки називають будь-яке відхилення від чіткої періодичності у розміщенні атомів. До макроскопічних дефектів належать тріщини, сторонні вкраплення та порожнини. Мікроскопічні дефекти – це порушення періодичності, розміри яких мають порядок кількох міжато-мних відстаней. Мікроскопічні дефекти поділяють на точкові та лінійні. Є три типи точкових дефектів:
Дефектом кристалічної ґратки називають будь-яке відхилення від чіткої періодичності у розміщенні атомів. До макроскопічних дефектів належать тріщини, сторонні вкраплення та порожнини. Мікроскопічні дефекти – це порушення періодичності, розміри яких мають порядок кількох міжато-мних відстаней. Мікроскопічні дефекти поділяють на точкові та лінійні. Є три типи точкових дефектів:
1) вакансія – це відсутність атома у вузлі ґратки;
2) заміщення – коли у вузлі ґратки міститься атом іншого сорту;
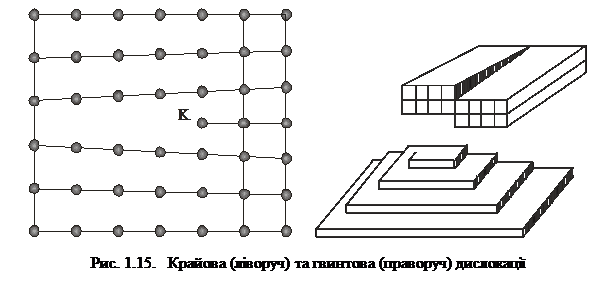
3) впровадження – коли атом іншого сорту міститься у міжвузлі кристалічної ґратки (рис. 1.14). Точкові дефекти порушують лише ближній порядок у кристалічній ґратці. На відміну від точкових, лінійні дефекти порушують дальній порядок у кристалі. Лінійні дефекти називають дислокаціями і поділяють на крайові та гвинтові. Крайову дислокацію можна уявити як додаткову півплощину, розміщену між атомними площинами кристала (див. рис. 1.14). Гвинтова дислокація утворюється внаслідок ковзання двох атомних півплощин на один період одна щодо одної (рис. 1.15).
Дислокації не можуть обриватися всередині кристала. Вони закінчуються на поверхні кристала, на межі зерна у полікристалічному зразку або ж мають вигляд замкненої петлі. Дислокації можуть суттєво впливати на механічні властивості твердих тіл.
Дата добавления: 2015-07-22; просмотров: 1530;
