Параллелизм. Рассмотрим случай, когда операнды Р и Q оператора || имеют неодинаковые алфавиты aР aQ.

Рассмотрим случай, когда операнды Р и Q оператора || имеют неодинаковые алфавиты aР 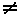aQ.

Когда такие процессы объединяются для совместного исполнения, события, содержащиеся в обоих алфавитах, требуют одновременного участия Р и Q. События же из алфавита Р, не содержащиеся в алфавите Q, не имеют никакого отношения к Q, который физически неспособен ни контролировать, ни замечать такие события. Такие события процесса P могут происходить независимо от Q. Аналогично Q может самостоятельно участвовать в событиях, содержащихся в его алфавите, но отсутствующих в алфавите Р.

Таким образом, множество всех событий, логически возможных для данной системы, есть просто объединение алфавитов составляющих ее процессов a(Р || Q) = aР 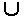aQ.

Законы

Формальное описание вышесказанного осуществляется с помощью следующих законов:

Пусть а (aР - aQ), b (aQ - aР) и {c, d} (aР aQ). Следующие законы показывают, каким образом процесс Р один участвует в событии a, Q один участвует в b, а c и d требуют одновременного участия P и Q.

L1А. (с Р) || (с Q)=с (Р || Q).

L1B. (с Р) || (d Q)=СТОП.

L2А. (a Р) || (с Q)=a (Р || (с Q)).

L2B.(с Р) || (b Q)=b ((с Р) || Q)..

L3.(a Р) || (b Q)=.(a (Р || (b Q)) | b ((a Р) || Q)).

Эти законы можно обобщить для общего случая оператора выбора:

L3.Пусть Р = (х: А Р(х)), Q = (y: B Q(y)). Тогда

Р || Q = (z: C (Р' || Q')),

где С = (A B) 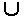(А - aQ) 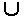(B - aP), P' = P(z), если z A, иначе P' = Р, а Q' = Q(z), если z B, иначе Q' = Q.

С помощью этих законов можно переопределить процесс, удалив из его описания, параллельный оператор, как это показано в следующем примере.

Пример 3.17.

Пусть aР = {a, c}, aQ = {b, c}, P = (a c P), Q = (c b Q). Тогда

Р || Q = (a c P) || (c b Q) = a ((c P) || (c b Q)) по L2A

= a c (P || (b Q)), по L1A (1)

(P || (b Q)) = a ((c P) || (b Q)) | b (P || Q) по L3

= a b ((c P) || Q) | b (P || Q)по L2B

= a b c (P || (b Q)) | b a c (P||(b Q)) по L1A и (1)

= mX.(a b c X | b a c X).

Отсюда следует, что

Р || Q = a c mX.(a b c X | b a c X).по (1)