Метод Верещагина.

Способ Максвелла — Мора в значительной степени вытеснил на практике непосредственное применение теоремы Кастильяно. В справочниках обычно приводятся таблицы интегралов 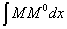для наиболее часто встречающихся типов нагрузки.

Наш соотечественник А. Н. Верещагин в 1924 г. предложил упрощение вычислений. Так как единичной нагрузкой бывает обычно либо сосредоточенная сила, либо пара сил, то эпюра 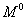оказывается ограниченной прямыми линиями. Тогда вычисление 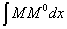при любом очертании эпюры М можно произвести следующим образом. Пусть эпюра М (Рис.3) имеет криволинейное очертание, а эпюра 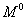— прямолинейное. Произведение Mdx можно рассматривать, как элемент 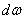площади эпюры М, заштрихованный на чертеже.

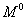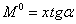Так как ордината равна , то произведение 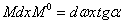, а весь интеграл 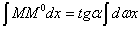представляет собой статический момент площади эпюры М относительно точки А, умноженный на .

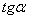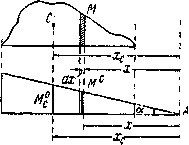
Рис.3. Расчетная модель метода Верещагина.

Но этот статический момент равен всей площади 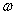эпюры М, умноженной на расстояние от ее центра тяжести 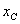до точки А. Таким образом,

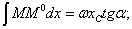
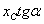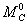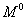но величина равна ординате эпюры под центром тяжести эпюры М. Отсюда

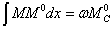
и искомое перемещение равно

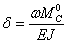
Таким образом, для определения перемещения 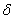надо вычислить 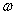— площадь эпюры М, умножить ее на ординату 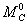эпюры от единичной нагрузки под центром тяжести площади 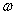и разделить на жесткость балки.

Определим этим способом угол поворота сечения D балки, изображенной на Рис.4, а; Балка загружена моментом М, приложенным в сечении В к консоли АВ. Эпюра М показана на Рис.4, б. Прикладываем в сечении D единичную пару, выбирая ее направление произвольно (Рис.4, в). Эпюра моментов от единичной нагрузки показана на рис.4, г. Так как М на участках DC и СВ равен нулю, то остается лишь один интеграл для участка АВ.

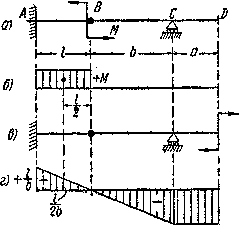
а) расчетная схема б)грузовая эпюра в)фиктивное состояние г) эпюра моментов от единичного момента

Рис.4. Иллюстрация метода Верещагина:

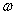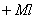Площадь равна ; ордината эпюры 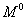под центром тяжести площади 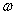равна отсюда искомый угол поворота 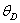равен

Знак плюс показывает, что вращение происходит по направлению единичной пары, т. е. по часовой стрелке.

Лекция № 35. Расчет статически неопределимых балок. Способ сравнения деформаций.