Написание формул

В математических формулах индексы и показатели степени долж­ны быть одинаковыми по величине и одинаково опущены или подняты по отношению к линии основной строки. Индексы, относящиеся к математическим знакам с пределами, должны быть написаны либо под (над) этими знаками, либо сбоку, например:

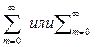
Скобки необходимо писать так, чтобы они полностью охватывали по высоте заключенные в них формулы. Открывающие и закрывающие скобки одного вида должны быть одинаковой высоты. В случае применения одина­ковых по начертанию скобок внешние скобки должны быть большего раз­мера, чем внутренние:

Y = k [а (b + сх)].

Знак корня должен быть такой величины, чтобы он охватывал все эле­менты подкоренного выражения. Знаки над буквами и цифрами необходимо писать точно над ними, на­пример:

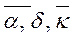
Основным знаком умножения является точка на средней линии ( 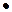). Знак умножения в виде косого креста (х) применяется чаще всего при переносе формулы с одной строки на другую на знаке умножения и для векторного произведения векторов. Точку как знак умножения не ставят перед буквен­ными обозначениями физических величин и между ними, перед скобками и после них, между сомножителями в скобках, перед дробными выражениями и после них или между несколькими дробями, написанными через горизон­тальную черту, перед знаком радикала, интеграла, а также перед аргументом тригонометрической функции, например:

Знак умножения следует применять между числовыми сомножителями (25 • 653,7) или когда вслед за аргументом тригонометрической функции стоит буквенное обозначение, а также для отделения сомножителей от вы­ражений, относящихся к знакам логарифма, интеграла, радикала и т.п., на­пример:

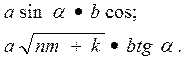
Если формула не умещается в одной строке, то ее частично переносят на другую строку. В первую очередь перенос следует делать на знаках ра­венства и соотношения между левой и правой частями формулы (= , ~ , > , < и т.д.), во вторую - на знаках сложения и вычитания (+, -), в третью - на знаке умножения применением косого креста (х) в конце одной строки и начале следующей строки. Не допускаются переносы на знаке деления.

При изложении математических выводов следует употреблять настоящее время глагола: "получаем", "находим", "определяем", "преобразуем" и т.д.

При расшифровке буквенных обозначений значения символов и числовых коэффициентов должны приводиться непосредственно под формулой в той последователь­ности, в какой они даны в формуле. После формулы ставят запятую. Пер­вую строчку экспликации начинают со слова "где", двоеточие после него не ставят.

Расшифровку значений символов располагают в виде колонки, символ отделяют от его расшифровки знаком тире. Размерность буквенного обозна­чения отделяют от текста запятой. Затем пишут численное значение симво­ла и при необходимости делают ссылку на источник. Пос­ле расшифровки каждого символа ставят точку с запятой. Колонки вырав­нивают по тире.

Не допускается употребление в тексте символов и условных буквенных обозначений без словесной расшифровки.

Затем формула записывается в численном выражении всех символов и коэффициентов и пишется конечный результат с размерностью без проме­жуточных вычислений.

Формулы должны нумероваться сквозной нумерацией арабскими цифрами, которые записывают на уровне формулы справа в круглых скобках. Первую формулу обозначают - (1). Ссылки в тексте на порядковые номера формул дают в скобках, напри­мер: ... в формуле (3).

Допускается нумерация формул в пределах раздела. В этом случае номер формулы состоит из номера раздела и порядкового номера формулы, разде­ленных точкой, например (2.1).

При указании величин с двумя пределами “от” и ”до” между ними ставят тире, многоточие или предлоги “от” и ”до”, а обозначение размерности ставят только один раз после второй цифры, например: 6…9 мм, в пределах от 5 до 10 град.

Если предельные числа представляют собой порядковые номера, то ин­тервалы чисел в тексте записывают только через дефис, например: рис.3-6.

Рядом стоящие цифровые величины отделяют одну от другой точкой с запятой, например: линейные размеры изменяются соответственно на 0.5; 1; 1,5; 5 мм.