Лекция 9

Математическая модель распространения звука в канале. Методы расчета глушителя шума вентилятора ТРДД.. Требуемая акустическая эффективность системы шумоглушения и методы ее определения.

Теоретическое решение задачи о снижении шума, распростра­няющегося в канале с равномерным потоком, основано на исполь­зовании волнового уравнения Блохинцева, которое в ци­линдрических координатах для акустического давления имеет вид

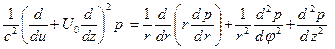(9.1)

где с — скорость звука; U₀ — постоянная скорость потока вдоль оси г, U₀ < c. Если решение уравнения (9.1) искать в форме волн, распространяющихся вдоль оси z (постоянная распростра­нения k_z) в виде:

,

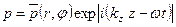то уравнение примет вид

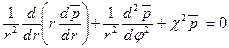(9.2)

где

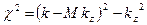(9.3)

, .

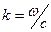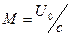Решение уравнения (9.2), полученное методом разделения переменных, имеет вид:

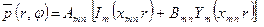(9.4)

где _Аmn, В_mn - произвольные постоянные, характеризующие зву­ковое поле в начальном сечении канала; m — число осцилляции звукового поля по азимуту; n - то же по радиусу; 1_т (xr) и У (xr) — соответственно функции Бесселя и Неймана целого порядка “m”..

При фиксированном значении “m” решение (9.4) называют азимутальной модой m-го порядка. Различным значениям “n” соответствуют разные радиальные моды.

Из уравне­ния (9.3) следует, что постоянная распространения может быть представлена в виде

(9.5)

Действительная часть k_z характеризует ослабление амплитуды звуковой волны на единицу длины пути и называется коэффициентом затухания. Мнимая часть постоянной распространения называется фазовой постоянной. Эта величина по смыслу аналогична волновому числу при некоторой фазовой скорости распространения, отличной от скорости звука..

Моды, у которых значения k_z действительны, называютcя распро­страняющимися или нормальными, а моды, у которых значения k_z мнимы,— нераспространяющимися или неоднородными. Знак действительной части корня в формуле (9.5) определяет направ­ление распространения волны; одинаковые знаки числа М и действительной части корня соответствуют распространению волны по потоку, противоположные - против потока. Действительная часть по­стоянной распространения определяет затухание в канале

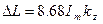(9.6)

Для решения уравнения Блохинцева можно воспользоваться граничным условием на стенке канала в виде линейной связи между давле­нием р и нормальной компонентой v_n акустической скорости, то есть импедансом стенки 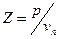, и условием непрерывности дав­ления и нормальной компоненты суммарной скорости среды на границе раздела, включающей и значение акустической скорости. В результате получим граничное условие на стенке канала

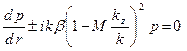(9.7)

где знак минус выбирается для цилиндрического канала радиуса г = а, знак плюс - для внутренней стенки кольцевого канала (r = b); .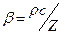

Характеристическое уравнение для определения собственных значений χ_mn в цилиндрическом канале получают из граничного условия (9.7) после подстановки в него выражения для звуко­вого давления р с учетом того, что в этом случае В_mn = 0.

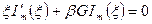, (9.8)

где

; (9.9)

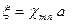
Аналогично для кольцевого канала характеристическое уравнение в общем случае имеет вид

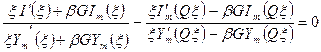, (9.10)

где Q = b/а - отношение внутреннего радиуса канала к внешнему. Урав­нения (9.8) и (9.10) совместно с (9.5) и (9.9) являются транс­цендентными уравнениями, решения которых полностью опреде­ляют нормальные моды цилиндрического и кольцевого каналов. В общем случае аналитических решений они не имеют, решения их могут быть получены только численным методом.

Исследования показывают, что в цилиндрическом канале в случае, когда частота высокочастотного 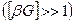звука намного превышает критическую, 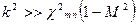, затухание звука при распространении против потока больше затухания его по потоку в отношении .

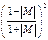В области низких частот (|βG|<<1) волна по потоку затухает сильнее, чем против потока. Учет пограничного слоя показывает, что его наличие на стенке канала ослабляет влия­ние потока на затухание звука. Наибольшее затухание в канале отмечается вблизи критической частоты, где оно не зависит от на­правления распространения звуковых волн и воздушного потока.

Приведенные выражения позволяют производить оптимизацию затухания звука в канале, то есть выбирать такой импеданс сте­нок канала, при котором будет обеспечено наибольшее снижение шума.

Акустический импеданс – это комплексное сопротивление, представляющее собой отношение комплексной амплитуды звукового давления к объемной колебательной скорости (произведению усредненной по площади колебательной скорости частиц среды на площадь, для которой определяется импеданс). В удельном акустическом импедансе рассматривается колебательная скорость в точке среды. Соотношение для импеданса системы представляет собой сумму действительной и мнимой частей:

,

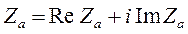где ReZa – действительная часть импеданса – активное акустическое сопротивление, связанное с диссипацией энергии в самой системе и с затратами энергии на излучение звука; Im Za – мнимая часть импеданса – реактивное акустическое сопротивление, обусловленное реакцией сил инерции (масс) или сил упругости. В задачах распространения звука в каналах с поглощающими стенками нередко используются акустические характеристики, являющиеся обратными по отношению к импедансу. Обратная величина акустического импеданса в комплексном виде называется адмитансом, а обратная величина действительной части импеданса называется проводимостью.

В достаточно длинном канале (или при равномерном рас­пределении звуковой энергии по волновым модам) ослабление интенсивности звука определяется затуханием наименее затухаю­щей моды из всех мод, возбуждаемых источником.

Как только моды с большим затуханием по амплитуде становятся много меньше наименее затухающей, они перестают давать вклад в суммарное затухание. В подобной ситуации увеличить суммарное зату­хание звука в канале возможно путем увеличения затухания наи­менее затухающей моды, подбирая для этого соответствующий импеданс стенок канала, то есть оптимизируя импеданс по этой моде.

Иное положение реализуется в случае короткого канала, где большое число мод дает вклад в суммарное затухание. В этом случае общее затухание определяется модой, которая наиболее сильно возбуждена, причем она не обязательно совпадает с наименее затухающей модой. Увеличение затухания наиболее возбуждаемой моды - основной метод увеличения суммарного затухания звуковой мощности в коротком канале.

В обоих случаях максимальное затухание отмечается, когда импеданс подобран из условия опти­мума при слиянии двух простых распространяющихся мод звуко­вой волны. При этом затухание двойной моды всегда больше, чем затухание менее ослабляемой из двух простых мод, которые могут образовать двойную моду.

Теоретическое решение задачи по определению импеданса стенок, который обеспечивает максимальное затухание шума в канале с потоком, показывает следующее. В цилиндрическом канале оптимальный адмитанс β₀ стенок канала может быть определен из уравнения:

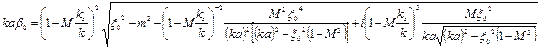
(9.11)

а двойные моды — из уравнения

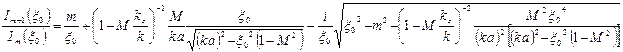
(9.12)

Методы практической реализации теоретически вычисленного им­педанса определяются типом применяемых звукопоглощающих конструкций. Например, для ЗПК из перфорированного листа с сотовым наполнителем геометрические пара­метры конструкции находятся для оптимального импеданса.

Сотовые ЗПК характеризуются следующими геометрическими параметрами (рисунок 9.1): диаметром отверстий перфорации - d; коэффициентом перфо­рации - F, выражающим отношение площади, занимаемой отвер­стиями, ко всей площади панели; толщиной перфорированной па­нели- t; глубиной воздушной полости - h (высотой сот), и поперечным размером сотовой ячейки - а.

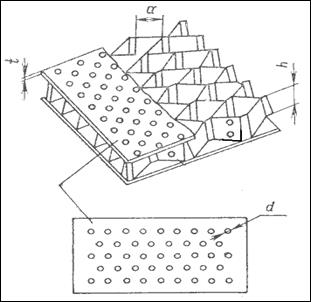
Рисунок 9.1

В каналах силовой установки существенно про­являются нелинейные эффекты, поэтому для описания поведения входного акустического импеданса сотовой ЗПК с заданными геометрическими параметрами недостаточно модели, представляю­щей собой набор резонаторов Гельмгольца. Необходимо учи­тывать вклад в импеданс различных физических факторов таких, как вязкость, влияние присоединенной массы в отверстиях перфо­рированной панели и эффект излучения энергии из отверстий, взаимодействие между ними, а также влияние высокого уровня звукового давления в падающей волне и скорости потока, сколь­зящего вдоль пористой поверхности сотовой ЗПК.

Взаимосвязь между входным акустическим импедансом однослойной сотовой ЗПК и ее геометрическими параметрами имеет вид

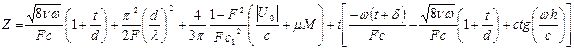(9.13)

где ν - кинематический коэффициент вязкости; IU₀I = амплитуда скорости в отверстиях перфорации; р — звуковое давление на поверхности пористой панели ЗПК;

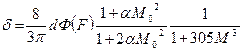
α — коэффициент; М — число Маха скорости потока; М₀ — число Маха, определенное для акустической скорости в отверстиях; μ — численный коэффициент, зависящий от параметров пограничного слоя; с₁ - коэффициент расхода, зависящий от числа Рейнольдса, определенного по диаметру отверстия, коэффициенту перфорации и отношению t/d, Ф (F) — функция Фока.

Теоретический метод выбора оптимального импеданса и гео­метрических параметров ЗПК, обеспечивающих наибольшее сни­жение уровня дискретных составляющих шума вентилятора, был проверен экспериментально. Получено хорошее соответствие рас­чета с экспериментом.

Основным недостатком описанных выше ЗПК является узкая полоса частот, в которой наблюдается эффективное снижение шума. Для расширения частотного диапазона возможно исполь­зование сотовых ЗПК с различной глубиной и коэффициентом перфорации, а также применение ЗПК более сложных схем, на­пример, двухслойных, состоящих из двух перфорированных листов и непроницаемого основания, разделенных двумя слоями сотового заполнителя.

Наконец, возможно использование так называемых объемных или «гомогенных» звукопоглощающих конструкций, включающих слои однородного пористого материала. Все пере­численные методы повышения эффективности глушителей связаны с усложнением их конструкции и технологии изготовле­ния, а также с ухудшением эксплуатационных свойств.

Повышения эффективности глушителя при любой конструк­ции ЗПК можно добиться путем размещения в каналах силовой установки дополнительных кольцевых или радиальных раздели­телей потока, облицованных ЗПК. Такие глушители могут обла­дать очень высокой акустической эффективностью, однако, они существенно усложняют конструкцию силовой установки, ухуд­шают ее параметры и надежность работы.