Лекция 5. Метрики структурной сложности программ.
Структурная сложность программ определяется:
· числом взаимодействующих компонент;
· числом связей между компонентами;
· сложностью взаимодействия компонент.
При функционировании программы разнообразие ее поведения и разнообразие связей между ее входными и результирующими данными в значительной степени определяется набором маршрутов(чередующихся последовательностей вершин и дуг графа управления), по которым исполняется программа.
Установлено, что сложность программного модуля связана не столько с размером (числом команд) программы, сколько с числом маршрутов ее исполнения и их сложностью.
Для повышения качества программы маршруты возможной обработки данных должны быть тщательно проверены при создании программы и тем самым определяют сложность ее разработки. Данную метрику сложности можно использовать для оценки трудоемкости тестирования и сопровождения модуля, а также для оценки потенциальной надежности его функционирования. Проведенные исследования подтверждают достаточно высокую адекватность использования структурной сложности программ для оценки трудоемкости тестирования, вероятности ненайденных ошибок и затрат на разработку программных модулей в целом.
Все маршруты исполнения программного модуля условно можноразделить на две группы:
· вычислительные маршруты;
· маршруты принятия логических решений.
Первая группа маршрутов включает в себя маршруты арифметической обработки данных и предназначена для преобразования величин, являющихся квантованными результатами измерения непрерывных физических характеристик (квазинепрерывных переменных).
Для проверки вычислительных маршрутов можно построить достаточно простую стратегию их проверки. Во всем диапазоне входных переменных нужно выбрать несколько характерных точек (предельные значения, значения в точках разрыва и несколько (1-3) промежуточных значений), для которых проверяется работоспособность программы. Предполагается, что в большинстве промежуточных точек программу можно не проверять из-за гладкости значений непрерывных переменных.
Сложность вычислительных маршрутов оценивается следующей формулой:
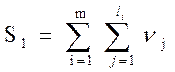 ,
,
где m – количество маршрутов исполнения программы;
li – число данных обрабатываемых в i-ом маршруте;
nj – число значений обрабатываемых данных j-го типа (2 £ nj £ 5)
Расчет сложности программы по данной формуле имеет значительную неопределенность из-за произвола в выборе количества значений nj при изменении входных данных. Поскольку доля вычислительной части во многих сложных программных комплексах обработки информации относительно невелика (общее число арифметических операций не выходит за предел 5–10%), вычислительные маршруты не определяют структурную сложность программ.
Сложность маршрутов принятия логических решенийоценивается формулой:
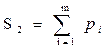 ,
,
где pi – число ветвлений или число проверяемых условий в i-ом маршруте.
Общая сложность программы определяется формулой:
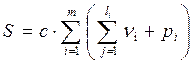 ,
,
где с– некоторый коэффициент пропорциональности, определение которого является сложной задачей.
Выделение маршрутов исполнения программы, минимально необходимых для ее проверки, и оценки структурной сложности могут осуществляться по различным критериям. Наилучшим, по-видимому,является критерий, позволяющий выделить все реальные маршруты исполнения программы при любых сочетаниях исходных данных. При этом формирование маршрутов зависит не только от структуры программы, но и от значений переменных в различные моменты времени. Такое выделение маршрутов трудно формализовать, и оно представляется очень трудоемким для оценки показателей сложности структуры.
Дата добавления: 2015-08-26; просмотров: 1454;
