Системы координат в пространстве.

Прямоугольная (декартова) система координатв пространстве возникает, если взяты три одинаковые взаимно перпендикулярные числовые оси - оси координат; которые пересекаются в точке O, называемой началом системы координат. Первую ось OX называют осью абсцисс, вторую ось OY - осью ординат, третью OZ - осью аппликат. Через каждые две (из трех) координатные оси проходит координатная плоскость.

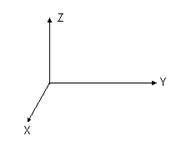
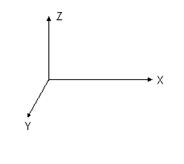
Существуют две, не сводящиеся друг к другу, системы координат: правая система координати левая система координат. Различить эти системы координат можно следующим образом: если посмотреть из любой положительной точки оси OZ на ось OY и ось OX окажется справа, то это правая система координат, если слева - левая (сравните рис.2.1а и рис.2.1б).

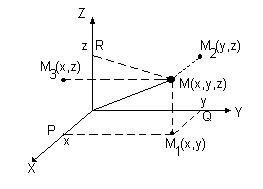
Каждой пространственной точке M можно сопоставить ориентированный отрезок OM, берущий начало в точке начала координат и оканчивающийся в точке M (рис.2.2). Такой отрезок называют радиус-вектором точкиM. Спроектируем точку М на оси координат. Каждой точке M соответствуют три точки на осях (на рис.2.2 P, Q, R), их координаты называют координатамиточкиM. Они однозначно определяют положение этой точки в выбранной системе координат. Наоборот, задав на каждой из осей координат по одной точке, например, P, Q, и R, мы определим одну и только одну точку в пространстве. Эта точка получается при пересечении трех взаимно перпендикулярных плоскостей PM₁MM₃, QM₁MM₂, RM₂MM₃, проходящих соответственно через точки P, Q и R параллельно осям координат. Расстоянием между двумя точкамиM(x₁,y₁,z₁) и N(x₂,y₂,z₂). в пространственазывается число d, равное длине отрезка прямой соединяющей эти точки

d = 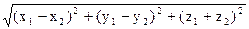. (2.1)

Например, расстояние между двумя точками M(2,-1,3) и N(-2,-1,0), согласно (3.16) равно

d =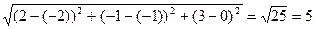

В пространстве всякая поверхность может рассматриваться как некоторое множество точек, между координатами которых установлены определенные соответствия

F(x,y,z) = 0 (2.2)