Modus Tollens
| Умова | |||||
| B | |||||
| Імплікація | A → B | ||||
| Висновок | |||||
| A |
У цьому випадку з істинності передумови та імплікації випливає істинність висновку. Наприклад, якщо «він не літає», то «це не літак».
Наведені вище дві (із багатьох існуючих) схеми висновку в двійковій логіці можна узагальнити на випадок нечіткості.
7.2. Правила висновку в нечіткій логіці
Припустимо, що наявні у правилах modus ponens і modus tollens судження характеризуються деякими нечіткими множинами. Далі буде записувати залежності типу «якщо А, то В» використовуючи службові слова мов програмування: if A then B.
| Modus Ponens | |||||
| Умова | x is А′ | ||||
| Імплікація if x is A then y is B | |||||
| Висновок | y is B′ | ||||
| Modus Tollens | |||||
| Умова | y is not B′ | ||||
| Імплікація | ifxisAthenyisB, | ||||
| Висновок | x is not A′ |
де А, А′, В, В′ – нечіткі множини, а x і y – нечіткі лінгвістичні змінні.
7.3. Нечітка імплікація
Функції належності в логічних висновках залежать від функції
належності 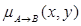 нечіткої імплікації
нечіткої імплікації 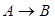 , рівнозначної деякому
, рівнозначної деякому
нечіткому відношенню 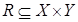 . Подамо різні способи задання функ-ції
. Подамо різні способи задання функ-ції 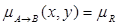 на основі відомих функцій належності
на основі відомих функцій належності 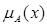 і
і 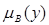 .
.
Нехай А і В – це нечіткі множини, 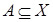 ,
, 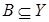 . Нечіткою імплі-кацією
. Нечіткою імплі-кацією 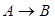 називають відношення R, визначене на X ×Y , що відповідає таким правилам:
називають відношення R, визначене на X ×Y , що відповідає таким правилам:
1. Правило типу «мінімум» (правило Мамдані)
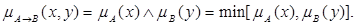
2. Правило типу «добуток» (правило Ларсена)
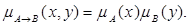
3. Правило Лукашевича
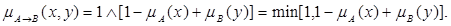
4. Правило типу «максимум-мінімум» (правило Заде)
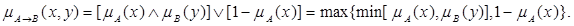
5. Бінарне правило (правило Кліна–Дейна)
µA→B (x, y) = [ 1- µA(x)]∨ µB (y) = max [ 1- µA(x),µB (y) ].
Окрім наведених є й інші означення нечіткої імплікації.
7.4. Нечіткий логічний висновок за методом Мамдані
Механізм нечіткого логічного висновку (inference) ґрунтується на
знаннях, сформованих спеціалістами цієї предметною галузі у вигляді сукупності нечітких породжувальних правил (правил логічного висновку):
if x1 is A1 and x2 is A2 and … xn is An then y is B
Частину правила перед ключовим словом then («то») називають
умовою або передумовою (antecendent), а завершальну частину «y є
В» – наслідком або висновком (consequent).
Проілюструємо механізм нечіткого логічного висновку на прикладі обчислень значень функції y = f (x1, x2). Припустимо, що маємо базу знань, яка складається з двох правил:
R1:if x1 is A11 and x2 is A22 then y is B1 ,
R2:if x1 is A12 or x2 is A22 then y is B2 ,
де Aij і Bi – це нечіткі множини, визначені для відповідних нечітких
змінних, котрі мають функції належностей µAij (x) і µBj (y).
Тепер за наданими значеннями x1 = x10 і x2 = x20 знайдемо конкретне y0 . Слід зазначити, що цей приклад легко узагальнити для довільної кілдькості вхідних (x) і вихідних (y) змінних.
Для логічного висновку приходимо за чотири кроки:
Крок 1. Введення нечіткості (fuzzification). Для чітко заданих вихідних значень розраховують ступені належності до окремих множин. Для розглядуваного прикладу визначають числові значення µA 1 j (x10) і µA2 j (x20) .
Нечітка імплікація. Знаходять функції належності перед
|
α = µA 1 j (x10) ∩ µA 2 j (x20) – для оператора and.
|
α = µA 1 j (x10) ∪µA 2 j (x20) – для оператора or.
|
Потім знаходять вислідні функції належності кожного правила
|
Нечітка композиція(aggregation). Знаходять вислідну функцію належності всієї сукупності правил при вхідних
сигналах x10 і x20 : µ∑(y) = µ1(y) ∪ µ2(y) .
Зведення до чіткості(defuzzification). Використовують, коли потрібно перетворити вихідну функцію належності у
|
|
|
y µ∑ (y)dy
|
|
|

µ∑ (y)dy
Як бачимо формула (7.1) досить важка для обчислень, тож часто в практичних розрахунках виконують наближені обчислення, замі нюючи інтеграли відповідними сумами.





µA11 µA21 µB1 





µA12 µA22 µB2


x10 x20 
µΣ 


Вхідні сигнали
y0
Рис. 7.1. Ілюстрація роботи алгоритму Мамдані
На практиці також часто використовуються такі методи:
– мінімальний максимум: результат ycl – найменша точка, в якій
µ∑(y) досягає максимуму;
– максимальний максимум: ycr – найбільша точка, в якій µ∑(y)
досягає максимуму;
|
|
– середній максимум: y0 = ycm = yi max , де yi max – точки, в яких 
µ∑(y) досягає локальних максимумів, m – кількість максимумів;
– зведення до чіткості по висоті: елементи області визначення R,
для яких значення функції належності, менші ніж певний рівень α, до
до уваги не беруть; чітке значення знаходять за такою

де Cα – нечітка множина α-рівня.
7.6. Нечіткий логічний висновок за методом Сугено
На практиці широко застосовують алгоритм нечіткого логічного
висновку Сугено (Sugeno), відомий також як алгоритм Такагі–Сугено–
Канга (TSK). Відмінною рисою цього алгоритму є простота обчислень.
Проджувальні правила в алгоритмі Сугено мають такий вигляд:
if x1 is A1 and x2 is A2 and … xn is An then y = fr (x1,..., xn) ,
де fr – звичайна чітка функція; r – номер правила.
Принципова відмінність від алгоритму Мамдані в цьому разі –
висновок, який подають у формі функціональної залежності.
Реалізація алгоритму Сугено складається із трьох кроків:
Крок 1. Введення нечіткості. Цілком аналогічне алгоритмові Мам-
дані.
Крок 2. Нечітка імплікація. Знаходяться функції належності перед-
умов кожного окремого правила за конкретних вхідних сиг-
налів xi0 :
αr , r =1, 2, ..., m,
де m – кількість породжувальних правил. У класичному ал-
горитмі Сугено логічна операція перетину реалізується як
min.
Крок 3. Зведення до чіткості. Визначається чітке значення вихідної
 змінної:
змінної:
Як функцію fr часто використовують поліноми нульового порядку:


Або першого порядку: , , де wr і prj – деякі сталі.
Їх називають алгоритмами Сугено нульового або першого порядку відповідно.
Зазначимо, що відомий алгоритм Ванга–Менделя відрізняється
від алгоритму Сугено нульового порядку тільки тим, що ступінь на-
лежності передумов правил у ньому знаходять за допомогою операції
множення.
Існує безліч алгоритмів нечіткого висновку, які відрізняються на-
бором вихідних правил, видом функцій належності, способами нечіт-
кої імплікації та композиції, а також методом зведення до чіткості.
8. СИНТЕЗ СИСТЕМ З НЕЧІТКОЮ ЛОГІКОЮ
Вступ
Під час розв’язування більшості прикладних задач регулювання,
інформацію, потрібну для побудови і реалізації системи керування,
можна поділити на дві частини:
– числову (кількісну), що отримується з вимірювальних датчиків;
– лінгвістичну (якісну), що надходить від експерта.
Значна частина нечітких систем регулювання використовує другий
вид знань, що частіше за все подають у формі бази нечітких правил.
У випадку, коли виникає потреба спроектувати нечітку систему,
але наявні лише числові дані, ми стикаємося з серйозними проблема-
ми. Один із способів їх розв’язання – це застосування так званих ней-
ро-нечітких (neuro-fuzzy) систем. Вони мають багато переваг, але їх
база правил повільно наповнюється знаннями в процесі ітеративного
навчання.
8.2. Нечіткі нейронні мережі
Основна перевага систем з нечіткою логікою – це здатність вико-
ристовувати умови і методи розв’язування задач, описані мовою, близь-
кою до природної. Однак класичні системи з нечіткою логікою, не-
здатні навчатися автоматично, мають недоліки. Набір нечітких пра-
вил, вид і параметри функцій належності, що описують вхідні і вихід-
ні змінні системи, а також вид алгоритму нечіткого висновку, виби-
раються суб’єктивно експертом-людиною, і вони не завжди відпові-
дають дійсності.
Для усунення вказаного недоліку був запропонований апарат не-
чітких нейронних мереж (fuzzy neural networks). Ці системи відомі та-
кож як адаптивні нейро-нечіткі системи висновку (Adaptive Neuro-Fuzzy Inference System, ANFIS).
Нечітка нейронна мережа – це багатошарова нейронна мережа, в якій шари виконують функції елементів системи нечіткого висновку. Нейрони такої мережі характеризуються набором параметрів, настроювання яких виконують під час навчання, як у звичайних ШНМ. На рис. 8.1 зображена нечітка ШНМ на базі алгоритму Сугено нульового порядку, за якого значення вихідної змінної обчислюють за фор-мулою
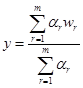
де αr – значення функцій належності передумов кожного окремого правила r за конкретних значень вхідних сигналів.
Шар 1 здійснює зведення до нечіткості.Нелінійні функціїµri (xi ),де r – номер продукційного правила, а i – номер компоненти вхідного вектора, відповідають функціям належності передумов правил. Настроювані параметри цього шару – параметри використовуваних функцій належності.
Шар 2 обчислює вислідні функції належності передумов нечіткихправил. У цьому випадку шар не має настроюваних параметрів.
Шар 3 (складається з двох нейронів)і виконує додавання і зважене додавання вихідних сигналів шару 2. Параметрами цього шару є вагові коефіцієнти wr .
Шар 4 реалізує операція ділення y = f1  f2.Він не містить настро-юваних параметрів.
f2.Він не містить настро-юваних параметрів.
Якщо в такій мережі використовувати функції належності гаус-сового типу, а для обчислення вислідних функцій належності переду-
мов правил (шар 2) – операцію множення замість операції «мінімум», то отримаємо досить поширену нечітку мережу Ванга–Менделя.
 Для мережі Ванга–Менделя можна аналітично подати градієнт функції похибки від параметрів мережі, що дає змогу використовувати для її навчання метод зворотного поширення похибки, котрий застосовують у багатошарових персептронах.
Для мережі Ванга–Менделя можна аналітично подати градієнт функції похибки від параметрів мережі, що дає змогу використовувати для її навчання метод зворотного поширення похибки, котрий застосовують у багатошарових персептронах.
Рис. 8.1. Нечітка нейронна мережа на основі алгоритму Сугено
8.3. Синтез нечітких правил на основі числових даних
Розглянемо один з найпростіших, але в той же час досить універсальний метод побудови бази нечітких правил на основі числових да-них. Переваги цього методу полягають в його простоті і високій ефективності. Крім того, він дає змогу об’єднувати числову інформацію, подану у формі даних для навчання, з лінгвістичною інформацією у вигляді бази правил доповненням наявної бази правилами, створеними на основі числових даних.
Припустимо, що ми створюємо базу правил для нечіткої системи з двома входами і одним виходом. Очевидно, для цього потрібні дані
| для навчання у вигляді множини пар (x1(i), x2 (i), d (i)) , де x1 (i), x2 (i) | – сиг- |
| нали, які подаються на вхід модуля нечіткого керування, а d (i) | – очі- |
куване (еталонне) значення вихідного сигналу.
Задача полягає у формуванні нечітких правил, щоб побудований на їх основі модуль керування під час отримання вхідних сигналів генерував коректні (що мають мінімальну похибку) вихідні сигнали.
Крок 1. Поділ простору вхідних і вихідних сигналів на інтервали
Припустимо, що нам відоме мінімальне і максимальне значення кожного сигналу. За ними можна визначити інтервали, в яких мітяться припустимі значення. Наприклад, для вхідного сигналу x1 такий інтервал позначимо [x1− , x1+ ] . Якщо значення x1− і x1+ невідомі, то можна скористатися навчаючими даними і вибрати з них відповідно
мінімальне і максимальне значення:
x1−=min(x1), x1+=max(x1).
Аналогічно для сигналу x2 визначимо інтервал [x2− , x2+ ] , а для бажаного вихідного сигналу d – інтервал [d −, d + ] .
Кожен визначений у такий спосіб інтервал поділимо на 2n + 1 (непарне число) інтервалів (відрізків), причому значення n для кожно-
го сигналу підбирається індивідуально, а відрізки можуть мати однакову або різну довжину. Окремі інтервали позначимо так: Sn (малий n), ... , Sn (малий1), M (середній), B1(великий1), ... , Bn (великий n).
На рис. 8.2 подано приклад такого поділу, де область визначення сигналу x1 розбита на п’ять інтервалів (n = 2), сигналу x2 – на сім ін-тервалів (n = 3), а область визначення вихідного сигналу y – на п’ять інтервалів (n = 2).
| µ(x1) | S2 | S1 | M | B1 | B2 | |

| x− | x1(1) | x1(2) x+ | x1 | |||
| µ(x2) | S3 | S2 | S1 M B1 | B2 B3 | ||

| x2− | x2(1) | x2(2) | x2+ | x2 | ||
| µ(d) | S2 | S1 | M | B1 | B2 | |

| d(1) | d(2) d + | y | ||
| d − |
Рис. 8.2. Поділ простору сигналів на інтервали
Кожна функція належності в даному прикладі має трикутну форму. Одна з вершин розміщена у центрі відрізка і їй відповідає значення функції, що дорівнює 1. Дві інших вершини лежать в центрах сусідніх відрізків. Їм відповідають значення функції належності, що дорівнюють 0. Зазначимо, що можна запропонувати багато інших способів поділу вхідного і вихідного простору на окремі відрізки і використовувати інші форми функцій належності.
Крок 2. Побудова нечітких правил на основі даних для навчання
Визначимо ступені належності даних для навчання кожного відрізка, виділеного на кроці 1.
Ці ступені будуть виражені значеннями функцій належності від-повідних нечітких множин для кожної групи даних.
Тепер співставимо дані для навчання (x1 (i), x2 (i), d (i)) з областями значень, в яких вони мають максимальні ступені належності. Наприклад, для випадку, показаного на рис. 8.2, x1 (1) має найбільший ступінь належності до інтервалу M, а x2 (1) – до інтервалу S1. Остаточно для кожної пари даних для навчання можна записати правило:
{x1 (1), x2 (1);d (1)}⇒
{x1 (1)[max = 0.8 in M], x2 (1)[max = 0.6 in S1 ];d (1)[max = 0.8 in M]}⇒
R(1): if x1 is M and x2 is S1 then y is M.
(8.1)
{x1 (2), x2 (2);d (2)}⇒
{x1 (2)[max = 0.8 in B1 ], x2 (2)[max =1 in M];d (2)[max = 0.8 in B1 ]}⇒
R(2): if x1 is B1 and x2 is M then y is B1.
Крок 3. Приписування кожному правилу ступеня істинності
Зазвичай є багато пар даних для навчання за кожною з яких можна сформулювати одне правило. Тому є висока ймовірність того, що
деякі з цих правил виявляться взаємовиключальними. Це стосується правил з одним і тим же посиланням (умовою), але з різними наслідками (висновками).
Один з методів вирішення цієї проблеми полягає у приписуванні кожному правилу так званого ступеня істинності з подальшим вибором серед правил, що суперечать одне одному, того, у якого цей ступінь виявиться найбільшим. Так не тільки вирішують проблему взає-мовиключальних правил, але й значно зменшується їх кількість. Для правила вигляду
R: if x1 is A1 and x2 is A2 then y is B
ступінь істинності, що позначається як SP(R), визначається як
SP(R) =µ A1 ( x1 ) µ A 2 ( x2 ) µB ( y) .
Наприклад, правило R(1) з (8.3) матиме ступінь істинності
SP(R 1 ) =µ M ( x1 ) µ S 1 ( x2 ) µ M ( y) = 0,8 ⋅ 0,6 ⋅ 0,8 = 0,384 .
Крок 4. Створення бази даних нечітких правил
Спосіб побудови бази нечітких правил подано на рис. 8.3.
| B3 | |||||||
| B2 | |||||||
| B1 | |||||||
| x2 M | B1 | ||||||
| S1 | М | ||||||
| S2 | |||||||
| S3 | |||||||
| S2 | S1 | M | B1 | B2 | |||
| x1 |


Рис. 8.3. Форма бази нечітких правил
Ця база зображена у вигляді таблиці, яку заповнюють нечіткими правилами таким чином: якщо правило має вигляд як, наприклад, правило R(1) у (8.1), то на перетині рядка S1 і стовпця M вписують назву нечіткої множини, отриманої в результаті, тобто М (відповідної вихідному сигналові y). Якщо є декілька нечітких правил з одним і тим же посиланням, то з них вибирають те, яке має найвищий ступінь істинності.
Крок 5. Зведення до чіткості
Наша задача зазвичай полягає у визначенні за допомогою бази правил відображення f : (x1, x2) → y , де y – вихідна величина нечіткої системи. Під час визначення кількісного значення керуючого впливу y для даних вхідних сигналів потрібно виконувати операцію зведеннядо чіткості.
Спочатку для вхідних сигналів (x1, х2) з використанням операції добутку об’єднаємо посилання (умови) k-го нечіткого правила. Так визначають ступінь активності k-го правила. Його значення знаходять за формулою
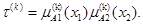
Для розрахунку вихідного значення y скористаємось способом зведення до чіткості за середнім центром:

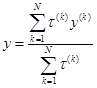 .
.
Розглянутий метод можна легко узагальнити для нечіткої системи з будь-якою кількістю входів і виходів.
8.4. Нечітка одноелементна модель
Ефективність застосування апарату нечіткої логіки ґрунтується на теоремах, аналогічних теоремам про повноту для нейронних мереж, суть яких полягає в тому, що система на основі алгоритму нечіткого виводу під час виконання визначених, але не дуже жорстких умов – це універсальний апроксиматор.
Найбільш простою системою апроксимації функцій є нечітка одноелементна модель (singleton fuzzy model), що ґрунтується на системі Сугено нульового порядку:
| ifxisAitheny=wi. | (8.2) |
До довільної функціональної залежності y = f(x) може бути застосована процедура кусково-лінійної апроксимації, як показано на рис. 8.4.
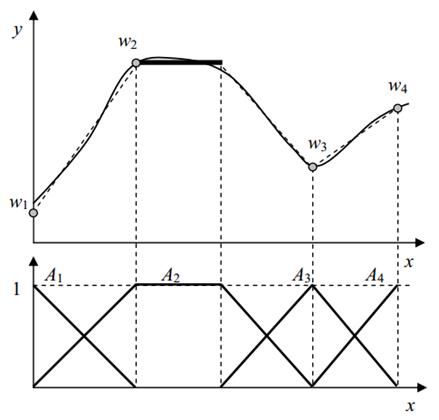
Рис. 8.4. Кусково-лінійна апроксимація і синтез множин
Вузли кусково-лінійної апроксимуючої функції відповідатимуть значенням коефіцієнта функції наслідку wi в моделі (8.2). Висновок і зведення до чіткості здійснюються за формулою
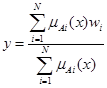 .
.
– добре прогнозовані апроксимаційні властивості;
– просте отримання параметрів.
Це викладення методів синтезу нечітких систем не можна вважати повним. Слід пам’ятати, що є багато алгоритмів і методів, які різняться набором вихідних правил, виглядом функцій належності, способами нечіткої імплікації і композиції, а також методом зведення до чіткості.
9. АЛГОРИТМИ ЗНАХОЖДЕННЯ ОПТИМАЛЬНИХ ТРАЄКТОРІЙ
9.1. Загальні положення
Серед всіх алгоритмів, що належать до стратегічного і тактичного рівнів структури інтелектуальної системи керування рухомим об’єктом, алгоритми пошуку оптимальної траєкторії, враховуючи обмеження, накладені перешкодами, є найбільш важливими для успішного розв’язання задач керування. В загальному вигляді такі задачі формулюються так: знайти шлях для руху об’єкта із початкового положення в кінцеве.Немає потреби нагадувати,що розв’язання такоїзадачі нетривіальне, це зумовлено різними перешкодами на шляху об’єкта, котрі блокують просування до цілі. Проте розрізняють безліч алгоритмічних підходів до розв’язання цієї задачі. Хоча не всі вони однаково ефективні, але їх послідовне розглядання дає змогу розібратися у проблемах, що виникають, і способах їх вирішення. У загальному вигляді алгоритм обходу перешкод такий:
покиціль не досягнутавибрати напрям руху до цілі
якщошлях вільний,
торухатись
інакшевибрати інший напрям відповідно
до вибраного алгоритму обходу перешкоди
Розглядувані алгоритми дають змогу обходити перешкоди під час руху за картою, заданою у вигляді прямокутного масиву значень, що характеризують ступінь «прохідності» цієї ділянки. Попри уявну обмеженість такого підходу, більшість алгоритмів можна узагальнити для інших способів задання простору руху.
9.2. Найпростіші алгоритми обходу перешкод
Найбільш прості алгоритми обходу перешкод – це метод руху у випадковому напрямку і метод відслідковування меж перешкод.
Дата добавления: 2015-08-26; просмотров: 1013;
