Конечно-разностная форма уравнения Навье-Стокса
Напряженное состояние жидкости. Законы движения и покоя жидкостей и газов основываются на законах механики сплошной среды, что позволяет рассматривать равновесие и течение жидкости в целом без учета механизма молекулярного движения.
В массе жидкости, которая рассматривается как сплошная среда, под влиянием внешних сил возникают соответствующие внутренние силы. Оценим порядок значений сил, действующих на элементарный изолированный объем, имеющий форму параллелепипеда со сторонами dx, dy, dz (см. рис. 3.2). Вся система движущейся массы отнесена к координатам x, y, z. На плоскостях граней изолированного параллелепипеда возникают напряжения. Составляющие напряжений, направленные перпендикулярно грани, называются нормальными напряжениями. Составляющие, находящиеся в плоскости граней, называются касательными напряжениями.
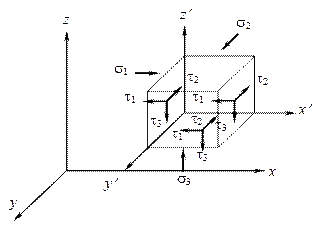
Рис. 3.2. Силы, действующие на элементарный изолированный объем
На поверхности граней элементарного параллелепипеда возникают три различных по величине касательных напряжения и три нормальных составляющих напряжений: вдоль осей x и y – напряжение t1, вдоль осей x и z – t2 и вдоль осей y и z – t3. Вдоль оси x действует нормальная составляющая напряжения s1, вдоль оси y – s2 и вдоль оси z – s3.
На массу жидкости, находящуюся в изолированном объеме, действуют массовые силы, которые пропорциональны третьей степени размера выделенного объема. При прохождении жидкости через изолированный элементарный объем происходит изменение количества движения массы жидкости. Это изменение вызывает соответствующий импульс сил, действующий на массу жидкости в изолированном объеме.
Изменение количества движения жидкости, протекающей через рассматриваемый неподвижный объем, пропорционально массе, заключенной в этом объеме и третьей степени его линейного размера. Силы, действующие на поверхности граней и равные возникающим напряжениям, умноженным на соответствующие площади, пропорциональны квадрату характерного линейного размера. При стягивании рассматриваемого элементарного объема в точку остаются только силы, связанные с возникающими в этой точке напряжениями.
Рассматривая элементарный объем, можно считать, что он находится в равновесии только под действием сил, возникающих за счет напряжений на его поверхности.
При течении реальных жидкостей в потоке возникают напряжения, которые раскладываются на нормальные и касательные составляющие к площадкам, на которых они действуют. В таком потоке можно рассматривать две системы напряжений: нормальные напряжения (давление), определяемые в любой точке потока; дополнительные напряжения, состоявшие из трех нормальных и трех касательных составляющих; эта система напряжений зависит в каждой точке потока от ориентации площадки, на которой возникают напряжения.
Выберем в точке, находящейся внутри потока и определяемой координатами x, y, z, систему прямоугольных координат x¢, y¢, z¢. В плоскостях координат возникнут кроме давления еще три нормальные s1, s2, s3 и три касательные t1, t2, t3 составляющие дополнительного напряжения. Значения дополнительного напряжения зависит от физических свойств и характера течения жидкости. Изолированная элементарно малая масса жидкости находится в момент времени t в начале координат. Элементарная масса имеет форму параллелепипеда с гранями, параллельными плоскостям координат. Стороны параллелепипеда имеют размеры dx, dy, dz. Рассмотрим проекцию сил, возникающих на гранях изолированного параллелепипеда под действием дополнительных напряжений, на ось x. В момент, когда он вместе с потоком движется мимо центра координат, на гранях, нормальных к оси x. действуют силы: 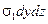 и
и 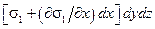 . Суммарная проекция силы, определяемая нормальными составляющими напряжения,
. Суммарная проекция силы, определяемая нормальными составляющими напряжения,
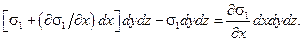
| (3.7) |
На гранях, параллельных плоскости координат x0z, действуют напряжения, а, следовательно, и силы вдоль оси x: 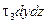 и
и 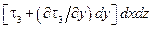 . Эти напряжения приводят к составляющей вдоль оси x, равной
. Эти напряжения приводят к составляющей вдоль оси x, равной 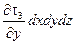 .
.
На гранях, параллельных плоскости координат x0y, на ось 0x проектируются силы 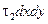 и
и 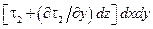 . Вдоль оси эти напряжения дадут составляющую
. Вдоль оси эти напряжения дадут составляющую 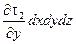 .
.
Суммарная составляющая сил, возникающих на гранях изолированного элемента жидкости за счет дополнительного напряжения в проекции на ось x,равна
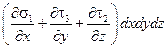 . .
| (3.8) |
Аналогично составляющие дополнительного напряжения, действующие на остальных гранях, в проекциях на оси 0y и 0z дадут составляющие сил:
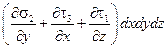 и и 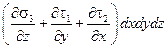 . .
| (3.9) |
Прибавляя эти силы, отнесенные к единице массы жидкости к правой части уравнений Эйлера, получим условия динамического равновесия в точке потока при течении реальной жидкости.
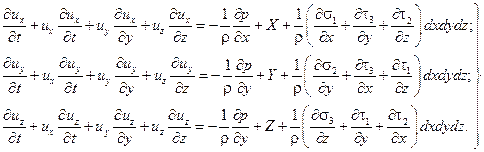
| (3.10) |
Определим теперь силы, возникающие в точке потока за счет вязкости. Проекция на ось 0x сил вязкости, отнесенных к единице объема и действующих в точке, определяемой в потоке координатами x, y, z. Проекция на ось 0x сил вязкости, отнесенных к единице объема и действующих в точке, определяемой в потоке координатами x, y, z:
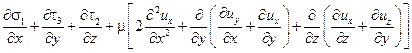 . .
| (3.11) |
Дифференцируя уравнение неразрывности по x, получим
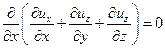 или или 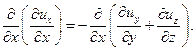
| (3.12) |
Тогда уравнение сил, возникающих за счет вязкости жидкости, равно
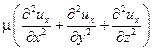 . .
| (3.13) |
Аналогично в проекции на оси 0y и 0z дополнительная проекция сил, которые следует учитывать при течении вязких жидкостей, составит:
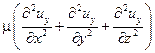 и и 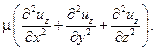
| (3.14) |
Уравнения Эйлера с учетом этих дополнительных сил примут вид:
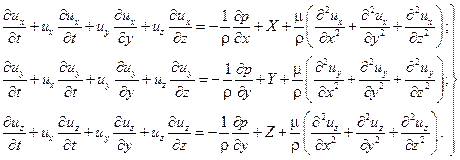
| (3.15) |
Полученная система уравнений называется уравнениями Навье-Стокса.
Уравнение Навье-Стокса, как и уравнение Зйлера, интегрируются только для некоторых частных случаев, но в последние годы, в связи с развитием различных методов решения подобных задач, полученные уравнения используются все чаще и являются идеальным инструментом, позволяющим получить хороший результат. Наиболее часто для решения уравнений Навье-Стокса применяются численные методы.
Дата добавления: 2015-08-26; просмотров: 1343;
