Метод Дельфи. Основные черты метода – регулярная обратная связь (участники экспертизы получают результаты обработки экспертных оценок по каждому туру)

Разработан в 1964 г. (амер. О.Хелмер, Т.Гордон). Сущность метода состоит в последовательном анкетировании мнений экспертов об объекте прогнозирования о формировании базы данных, отражающей индивидуальные оценки экспертов.

Основные черты метода – регулярная обратная связь (участники экспертизы получают результаты обработки экспертных оценок по каждому туру), анонимность (участники экспертизы не располагают информацией о том, кто из них давал те или иные оценки), групповой ответ (статистическая обработка результатов экспертизы позволяет уменьшать разбросы индивидуальных оценок и получать групповой ответ, в котором отражено мнение каждого эксперта).

Обработка результатов экспертизы на каждом этапе производится на основе следующих принципов:

- вопросы в анкетах формулируются в количественных шкалах

- опрос производится в несколько туров, в ходе которых вопросы и ответы все более уточняются

- все эксперты знакомятся после каждого тура с результатами опроса

- эксперты, выразившие крайние отклонения от мнения большинства, обосновывают свои мнения и оценки

- обработка результатов экспертизы на каждом этапе производится с целью получения обобщающих характеристик

Ø Метод сценариев и др.

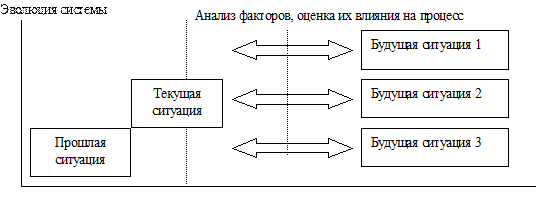
Это метод декомпозиции (т.е. упрощения) задачи прогнозирования, предусматривающий выделение набора отдельных вариантов развития событий (сценариев). При этом каждый отдельный сценарий должен допускать возможность достаточно точного прогнозирования, а общее число сценариев - быть обозримым.

В конкретной ситуации сама возможность подобной декомпозиции не всегда очевидна. При применении метода сценариев необходимо осуществить два этапа исследования:

· построение исчерпывающего, но обозримого набора сценариев;

· прогнозирование в рамках каждого конкретного сценария с целью получения ответов на интересующие менеджера вопросы.

Методы моделированияоснованы на исследовании статистических зависимостей между изучаемыми факторами и характеристиками. Для этого используются методы математической статистики.

Корреляционный анализ – основан на изучении связей между математическими ожиданиями случайных величин. Теснота связей оценивается коэффициентом корреляции.

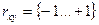
Если значение коэффициента корреляции равно 0, то связи между переменными х и у нет. Если равно +1, то корреляция положительная (рост одной переменной вызывает рост другой). Если равно –1, то корреляция отрицательная. Метод дает возможность проверить различные гипотезы (предположения) о связях между различными техническими и экономическими явлениями.

Регрессионный анализ устанавливает количественное соотношение между величинами случайного процесса. Полученные соотношения в форме уравнений регрессии часто используются в экономическом анализе.

Пример. В 20-30 годах попытка связать два фактора производства в форме уравнений регрессии (производственная функция Кобба-Дугласа)

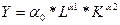
где Y – конечный продукт, L – интенсивность трудовых затрат, К – интенсивность капитальных затрат, a0, a1, a2 – коэффициенты уравнения регрессии.

Дисперсионный анализ – устанавливает зависимость результатов наблюдения от разных, одновременно действующих факторов, и позволяет проводить выбор наиболее значимых из них, отбрасывая несущественные.