Электромеханические и пьезоэлектрические фильтры

Физические основы работы электромеханических, пьезоэлектрических и акустоэлектронных фильтров. Резонансные контуры, входящие в состав электрических фильтров, трудно сделать высокостабильными, высокодобротными и в то же время малогабаритными, поэтому, не смотря на простоту их изготовления и возможность выбора вида частотной характеристики при увеличении числа контуров, эти фильтры используются ограниченно.

Указанные обстоятельства обусловили появление фильтров, основанных на принципе механических упругих колебаний и механического резонанса. Широкое применение таких фильтров объясняется тем, что скорость распространения упругих колебаний в твердом теле примерно в 100 тыс. раз меньше скорости распространения электромагнитных волн. Это позволяет использовать очень компактные механические резонаторы с распределенными параметрами, обладающие чрезвычайно малыми потерями, т. е. весьма высокой добротностью, достигающей 10³…10⁴. Однако для применения этих фильтров в электронной аппаратуре необходим переход от электрических колебаний и сигналов, действующих в цепях этой аппаратуры, к акустическим (упругим) колебаниям в механических резонаторах и последующий переход от акустических к электрическим.

Для этого преобразования используются известные из физики эффекты взаимодействия электрических или магнитных полей и механических деформаций и напряжений, например пьезоэффект и магнитострикционный эффект. Особенности и свойства таких преобразователей существенно зависят от того, какой эффект при этом используется. Часто название эффекта, на котором основано преобразование, применяется при классификации фильтров. Например, различают пьезокерамические, пьезокварцевые, магнитострикционные фильтры и т. д.

Полагая, что преобразования электрических колебаний в механические и обратно произведены, рассмотрим физическую сущность фильтрации в механических системах. Как известно из радиотехники, колебания и резонансы могут возникать в цепях с сосредоточенными (LC-фильтры) и с распределенными (длинные линии) параметрами. Аналогично обстоит дело и при механических колебаниях. Они могут появляться в системах с сосредоточенными параметрами, например, в механических системах, имеющих массу (груз) и упругость (пружину). Однако такие системы обладают низкой резонансной частотой колебаний и не могут использоваться для создания фильтров на радиочастотах. Их изучение имеет большое значение для исследования действия механических возмущений на конструкции РЭА и ее элементы, а также для амортизации. Механические колебания возникают и в системах с распределенными параметрами. Простейшими механическими с распределенными параметрами являются брусок, пластина, стержень, струна, диск и т. д.

Для выяснения физической сущности механического резонанса остановимся на простейших механических продольных объемных колебаниях, которые возникают и распространяются в стержнях. Анализ распространения упругих волн приводится с использованием волнового уравнения

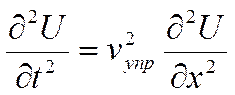, (5.21)

где U – переменное напряжение (деформация); t – время; x – координата; v_упр – скорость распространения волны в материале. В стержнях из упругих материалов, какими являются металлы, используемые в резонаторах, скорость распространения объемной продольной волны

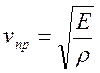, (5.22)

где E – модуль упругости; ρ – плотность материала.

В связи с конечной скоростью распространения упругих колебаний вдоль стержня можно ввести понятие длины акустической волны

. (5.23)

Длина волны на разных частотах при скорости 5000 м/с, характерной для используемых материалов, дана в табл. 5.3. Как видно, длина упругой волны в металле на радиочастоте составляет несколько миллиметров.

При длине бруска l_бр=λ_а /2 наступает резонанс и затухание колебаний в этом случае мало. Если колебания возбуждаются внешней силой, то напряжения и деформации будут максимальны. Если для примера взять распределение упругости напряжений и деформаций в резонирующем бруске, то края бруска в процессе колебаний перемещаются, в то время как центр бруска, в котором наблюдаются наибольшие внутренние напряжения, остается в покое. Пользуясь соотношением l_бр=λ_а /2, можно от длины волны перейти к резонансной частоте. Тогда получим

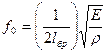. (5.24)

Кроме основной резонансной частоты могут наблюдаться резонансы на кратных частотах (гармониках), когда на длине стержня укладывается целое число m полуволн.

В механических фильтрах используются изгибные, продольные, крутильные, поперечные, сдвиговые и поверхностные (волны Рэлая и Лява) волны. Деформации волн и направления их распространения приведены на рис. 5.7, где а) – изгибное, б) – продольное, в) – поперечное, г) – крутильное и д) – поверхностное колебания. Стрелками показаны деформации и направления распространения волны; λ_а – длина волны, которая определяется следующими скоростями распространения: v_изг, v_пр, v_поп, v_кр, v_пов. Эти скорости зависят от свойств материалов, в основном, от модуля упругости Е и плотности материала ρ. Скорости для каждого вида колебаний различны и могут отличаться в два раза.

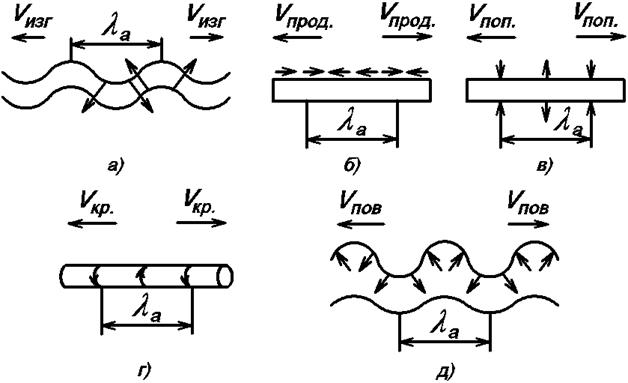
Рис. 5.7

В пьезоэлектрических фильтрах механические колебания возбуждаются в результате пьезоэффекта, но эти колебания в другие резонирующие элементы не передаются. Эффект фильтрации достигается вследствие того, что механический резонанс изменяет электрические характеристики цепи преобразователя электрических колебаний в механические.

Основной положительной особенностью фильтров на поверхностных акустических волнах является то, что их изготовление основывается на технологии микроэлектроники (формирование пленок с разными свойствами). По этому широкое развитие получило новое направление, относящееся к функциональной микроэлектронике, известное как актустоэлектроника.

Рассмотрим работу магнитострикционных преобразователей. Из физики известен эффект Джоуля, который состоит в том, что если некоторые ферромагнитные тела поместить в магнитное поле, то происходит намагничивание, сопровождающееся возникновением внутренних механических сил в теле. В результате меняются его геометрические размеры.

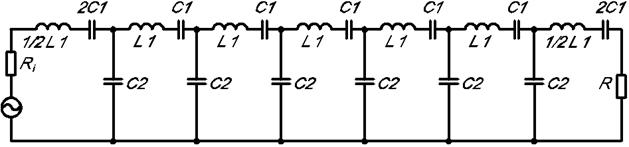
Рис. 5.12

Пример приближенной эквивалентной схемы электромеханического фильтра приведен на рис. 5.12, где L1 и C1 – эквивалентные параметры резонатора, а C2 – эквивалентные связи. Число звеньев и степень связи, полученные при электрическом расчете, реализуются при конструировании фильтра. При конструировании резонаторов необходимо определить их материал и геометрические размеры, а вид колебаний выбирается заранее.

Пьезокварцевые и пьезокерамические фильтры. Значительно большие возможности дают такие принципы преобразования электрических колебаний в механические или такие принципы связей элементов электрических цепей с механическими резонаторами, при которых активные потери при преобразовании получаются малыми. Такими особенностями обладают преобразователи, в которых вследствие пьезоэффекта происходит возбуждение упругих механических колебаний. В этих преобразователях получается своеобразный конденсатор, к обкладкам которого подается напряжение переменного тока.

Схема замещения пьезоэлектрического резонатора, содержащая кроме С₀ ветвь LCR_р , отображающую действие резонатора, а также зависимость модуля сопротивления |Z|, полученную экспериментально с учетом потерь, и зависимость реактивного сопротивления х резонатора при отсутствии потерь приведены на рис. 5.17. Частота f_p соответствует частоте последовательного резонанса между индуктивностью L и емкостью С: f_p=1/2π 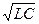. При этом сопротивление резонатора резко уменьшается, достигая сопротивления резонатора резко уменьшается, достигая сопротивления R_p – активного сопротивления, отображающего наличие потерь при колебаниях пластины резонатора.

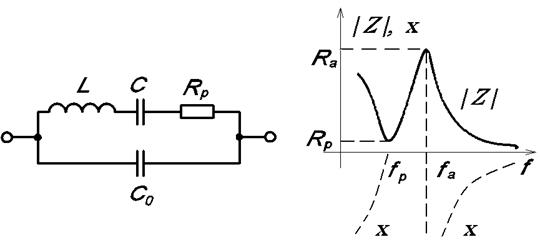
Рис. 5.17