Лекция №13.
Обмотка статора может быть соединена звездой или треугольником. Схема соединения зависит от расчётного напряжения двигателя и номинального напряжения в сети.
Допустим линейное напряжение 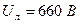 , а двигатель рассчитан для включения в сеть с напряжением
, а двигатель рассчитан для включения в сеть с напряжением 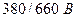 , тогда обмотку статора следует соединять звездой, так как в этом случае
, тогда обмотку статора следует соединять звездой, так как в этом случае 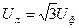 , то есть
, то есть 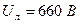 , а
, а 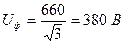 .
.
Если же 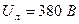 , то обмотку статора следует соединить треугольником. В этом случае
, то обмотку статора следует соединить треугольником. В этом случае 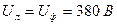 .
.
Для осуществления таких соединений на корпусе двигателя имеется клеммная коробка, куда выведены начала и концы фаз.

Формула для нахождения частоты вращающегося поля.
Пусть на статоре всего три катушки.

 Рассмотрим момент
Рассмотрим момент 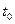 , при котором
, при котором 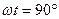 , в этом случае ток
, в этом случае ток 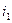 положителен, а токи
положителен, а токи 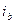 и
и 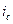 отрицательны. Если ток положителен, его направление примем от начала обмотки к её концу.
отрицательны. Если ток положителен, его направление примем от начала обмотки к её концу.
Для определения направления поля применяется правило правоходового винта.
Вектор магнитного поля направлен от северного полюса 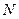 к южному полюсу
к южному полюсу  . Если на статоре три катушки, то образуется одна пара полюсов, то есть
. Если на статоре три катушки, то образуется одна пара полюсов, то есть 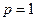 .
.
Через время, равное периоду 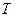 ось поля займёт первоначальное положение, следовательно, за период
ось поля займёт первоначальное положение, следовательно, за период 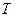 поле делает один полный оборот. Так как
поле делает один полный оборот. Так как 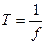 , следовательно,
, следовательно, 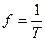 .
.
Частота 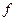 - число полных колебаний или оборотов в секунду.
- число полных колебаний или оборотов в секунду.
Чаще частоту вращения поля выражают в оборотах в минуту:  .
.
Если число катушек в каждой фазе увеличить, а сдвиг фаз между токами оставить равным 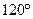 , то частота вращения поля измениться:
, то частота вращения поля измениться:  .
.
Зависимость частоты вращения поля от числа катушек:
| Число катушек в статоре | |||||
| Число пар полюсов | |||||
| Угол в пространстве между катушками | 120° | 60° | 40° | 30° | 24° |
| Частота вращения поля |
ЭДС статора и неподвижного ротора. Режим холостого хода.
Обмотка ротора разомкнута. Ток в ней равен нулю. Вращающий момент также равен нулю, то есть ротор остаётся неподвижным. Частота индуцированной ЭДС в обмотке ротора равна частоте питающей сети. При этом магнитный поток, пронизывающий каждый виток в обмотке статора и ротора, меняется по синусоидальному закону: 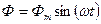 . Действующее значение ЭДС, которая индуцируется в каждом витке, по аналогии с трансформатором можно найти по формуле
. Действующее значение ЭДС, которая индуцируется в каждом витке, по аналогии с трансформатором можно найти по формуле 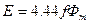 . ЭДС, которая индуцируется в обмотке статора, можно приблизительно найти по формуле:
. ЭДС, которая индуцируется в обмотке статора, можно приблизительно найти по формуле: 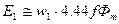 , а ЭДС, которая индуцируется в обмотке неподвижного ротора, приблизительно определяется по следующей формуле:
, а ЭДС, которая индуцируется в обмотке неподвижного ротора, приблизительно определяется по следующей формуле: 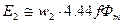 .
.
Коэффициент трансформации: 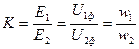 .
.
Ток в обмотке ротора также будет равен нулю, если обмотка замкнута, а скорость вращения ротора 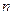 достигнет
достигнет 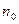 . Такой режим называется режимом идеального холостого хода. При этом в обмотке статора также протекает ток
. Такой режим называется режимом идеального холостого хода. При этом в обмотке статора также протекает ток 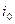 , который достигает 20-40 процентов от номинального тока.
, который достигает 20-40 процентов от номинального тока.
ЭДС вращающегося ротора.
Если обмотку фазного ротора замкнуть накоротко или на какое-либо сопротивление, то по ней потечёт ток 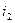 , что приведёт к возникновению силы, действующей на проводник с током, то есть ротор будет разгоняться и при полной или номинальной нагрузке величина скольжения
, что приведёт к возникновению силы, действующей на проводник с током, то есть ротор будет разгоняться и при полной или номинальной нагрузке величина скольжения  станет равной 2-8 процентам.
станет равной 2-8 процентам.
Определим частоту тока в обмотках вращающегося ротора:
 ;
;  ;
; 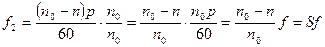 .
.
Таким образом, во вращающемся поле 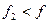 .
.
Если частота сети 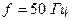 , а величина скольжения
, а величина скольжения  лежит в пределах
лежит в пределах 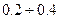 , то при номинальной нагрузке
, то при номинальной нагрузке 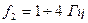 .
.
ЭДС, которая возникает в подвижном роторе можно определить по следующей формуле: 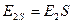 , где
, где 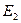 - ЭДС, возникающая в неподвижном роторе. Таким образом, ЭДС во вращающемся роторе значительно меньше ЭДС в неподвижном роторе.
- ЭДС, возникающая в неподвижном роторе. Таким образом, ЭДС во вращающемся роторе значительно меньше ЭДС в неподвижном роторе.
Токи ротора, помимо участия в создании общего магнитного потока, образуют также токи рассеивания. Следовательно, возникает ЭДС рассеивания. Действие этой ЭДС учитывается следующим образом: 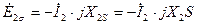 . Можно записать выражение для тока во вращающемся роторе:
. Можно записать выражение для тока во вращающемся роторе: 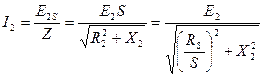 , где
, где 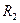 - активное сопротивление обмотки ротора.
- активное сопротивление обмотки ротора.
В момент пуска двигателя величина скольжения  равна 1, а ток
равна 1, а ток 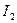 достигает своего максимального значения, и становится равен пусковому току
достигает своего максимального значения, и становится равен пусковому току 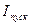 . Обмотка ротора электрически не связана с внешней цепью. Ток в ней появляется за счёт наведённых ЭДС, поэтому уравнение напряжений для цепи вращающегося ротора будет иметь следующий вид:
. Обмотка ротора электрически не связана с внешней цепью. Ток в ней появляется за счёт наведённых ЭДС, поэтому уравнение напряжений для цепи вращающегося ротора будет иметь следующий вид: 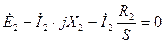 .
.
Уравнение напряжение обмотки статора совпадает с уравнением напряжения для обмотки трансформатора: 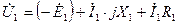 . Уравнение токов обмотки статора также аналогично уравнению токов обмотки трансформатора:
. Уравнение токов обмотки статора также аналогично уравнению токов обмотки трансформатора: 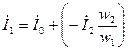 .
.
Действительную цепь вращающегося ротора заменяют энергетически эквивалентной цепью заторможенного (неподвижного) ротора с частотой 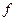 . При этом ток и мощность, потребляемые двигателем из сети, а также электромагнитная мощность, передаваемая ротору, остаются неизменными, поэтому можно изобразить схему замещения эквивалентного неподвижного ротора.
. При этом ток и мощность, потребляемые двигателем из сети, а также электромагнитная мощность, передаваемая ротору, остаются неизменными, поэтому можно изобразить схему замещения эквивалентного неподвижного ротора.
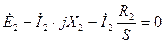
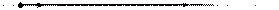 .
.
Активное сопротивление:
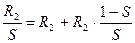 .
.
Механическая нагрузка асинхронного двигателя при анализе условно заменяется эквивалентной электрической нагрузкой, включённой в сеть ротора. Если сделать привидение параметров обмотки ротора к числу витков статора, то получается полная схема замещения одной фазы трёхфазного асинхронного двигателя.
 В электрическом отношении асинхронный двигатель подобен трансформатору, работающему на чисто активную нагрузку.
В электрическом отношении асинхронный двигатель подобен трансформатору, работающему на чисто активную нагрузку.
Электрические потери – потери в обмотках.
Электрические потери в обмотках статора можно определить по следующей формуле:  .
.
Электрические потери в обмотке ротора определяются по формуле:  .
.
Тепловые потери в сопротивлении 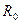 равны магнитным потерям в стальном магнитопроводе статора, то есть
равны магнитным потерям в стальном магнитопроводе статора, то есть 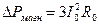 .
.
Тепловые потери в сопротивлении 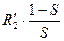 числено равны электрической энергии фактически преобразованной в механическую работу, то есть:
числено равны электрической энергии фактически преобразованной в механическую работу, то есть: 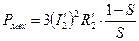 .
.
От статора к ротору передаётся электромагнитная мощность, которую можно определить по формуле: 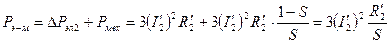 .
.
Возьмём отношение: 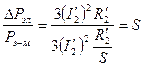 , следовательно,
, следовательно, 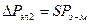 .
.
Потери в цепи ротора прямо пропорциональны скольжению, поэтому двигатели с большими номинальными скольжениями имеют большие потери, а следовательно низкий КПД.
Электромагнитный вращающий момент.
Механическую работу можно найти по формуле: 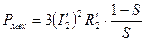 . Кроме того, эту работу можно найти следующим образом:
. Кроме того, эту работу можно найти следующим образом: 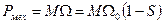 , где
, где 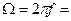
 . Если приравнять да этих выражения, получим следующее выражение для момента:
. Если приравнять да этих выражения, получим следующее выражение для момента: 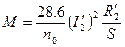 . Если это выразить через напряжение с учётом упрощённой схемы замещения и выразить ток
. Если это выразить через напряжение с учётом упрощённой схемы замещения и выразить ток 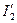 через напряжение на фазе, то можно получить следующее выражение для момента:
через напряжение на фазе, то можно получить следующее выражение для момента: 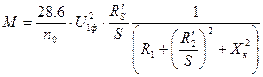 . При заданном значении напряжения
. При заданном значении напряжения  на фазе, вращающий момент двигателя зависит только от скольжения
на фазе, вращающий момент двигателя зависит только от скольжения  или от скорости вращения ротора
или от скорости вращения ротора 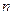 , так как
, так как 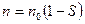 .
.
Механические характеристики.
Задаваясь различными значениями величины скольжения  в пределах от 0 до 1, пользуясь полученной формулой можно построить зависимость
в пределах от 0 до 1, пользуясь полученной формулой можно построить зависимость 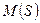 .
.

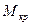 - максимальный (критический) момент.
- максимальный (критический) момент.
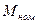 ,
,  - номинальные момент и скольжение, когда двигатель работает при полной нагрузке.
- номинальные момент и скольжение, когда двигатель работает при полной нагрузке.
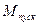 - момент при пуске.
- момент при пуске.
С помощью этого графика, учитывая соотношение 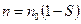 , строят зависимость
, строят зависимость  .
.
Эти зависимости 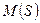 и
и  называют механическими характеристиками двигателя.
называют механическими характеристиками двигателя.
Вращающий момент и скольжение соответствующие работе двигателя при полной нагрузке называются номинальными моментом и скольжением.
Естественные механические характеристики – механические характеристики, построенные для случая, когда напряжение на зажимах двигателя равно номинальному, и в цепях двигателя отсутствуют какие-либо добавочные сопротивления.
Реостатные механические характеристики – механические характеристики, полученные при включении реостата в цепь фазного ротора.
Дата добавления: 2015-08-21; просмотров: 553;
