Способы решения обратной задачи.
В основе простейших методов решения обратных задач гравиразведки лежат те же аналитические соотношения между характером поля и параметрами возмущающих тел правильной формы, которые мы рассматривали выше. Это аналитические формулы для геологических тел, по форме близкие к шару, горизонтальному и вертикальному круговому цилиндрам, конечным призмам и т.д.
Изменяя параметры той или иной формы тела, можно получить целый альбом теоретических кривых, соответствующий той или иной геологической ситуации.
При решении обратной задачи практически можно найти такие теоретические кривые, которые будут наиболее близко соответствовать наблюденным графикам поля. Параметры объекта, которые обусловили теоретическую кривую, по характеру близкую к наблюденному полю, можно в первом приближении отнести к реальному геологическому объекту, обусловившему практический график поля. Так в принципе, можно решать обратную задачу гравиразведки с помощью атласа теоретических кривых.
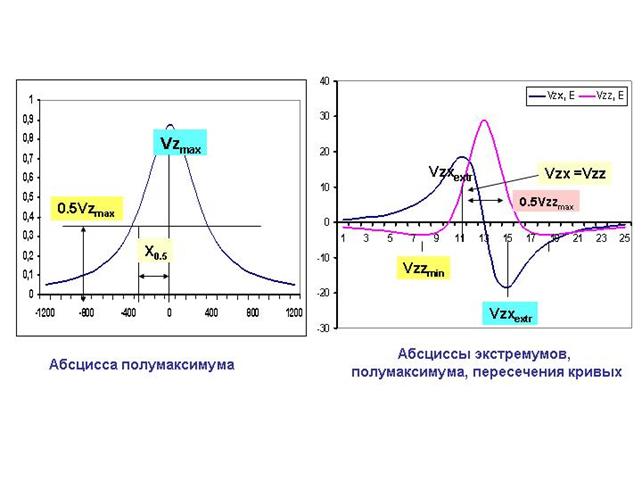
Рис. 2.34. Положение абсцисс характерных точек графиков, используемых при количественной интерпретации
Однако чаще при интерпретации графиков наблюдаемого гравитационного поля используют так называемый метод характерных точек. Правильнее было бы называть его "метод абсцисс характерных точек графиков поля". В основе этого метода лежит связь между численными значениями какого-либо параметра объекта (например, глубины его залегания) и абсциссами наиболее характерных точек графика поля: полумаксимума D g или V ZZ, перехода через нулевую ординату, экстремумов, точек равных значений VZZ и V ZX и т.д.
Естественно, что эти соотношения для разных форм объектов будут разные (рис. 2.34), оставаясь постоянными для разных избыточных плотностей. Зная глубину залегания объекта, можно найти другие его параметры, избыточную массу, сечение, полную массу (запасы) и т.д. например, зная глубину центра масс геологического объекта конечных размеров (по форме близкого к шару), можно найти его избыточную массу, радиус сечения и запасы, из соотношения:
Dgmax =k*M / h2; (2.81)
Отсюда избыточная масса будет равна M=Dgmax*h2 / k;
Объем шара V= 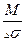 и радиус его эпицентрального сечения R=
и радиус его эпицентрального сечения R=  . В итоге полная масса шара будет равна P=V*s , где Ds - избыточная плотность объекта, s - истинная плотность вещества шара (руды), Р- запасы руды.
. В итоге полная масса шара будет равна P=V*s , где Ds - избыточная плотность объекта, s - истинная плотность вещества шара (руды), Р- запасы руды.
Характерные точки гравитационного поля простейших геометрических тел
(для эпицентрального профиля)
Таблица 2.4.
| № п/п | Форма объекта | По графику поля | Абсцисса характерной точки | Величина | |||||
| полумак- симума | перехода ч-з ноль | Vzx=VD | X | Y | |||||
| max | min | max | min | ||||||
| 1. | Однородный шар | Dg | ±0,77h | — | — | — | кМ*h-2 | — | |
| Vzx | — | - h | -0,51h | +0,51*h | ±0,858*kMh-3 | ||||
| Vzz | 2кМ*h-3 | -0,036кМ*h-3 | |||||||
| VD | — | — | - h | ±0,81*h | -0,558*kMh-3 | ||||
| 2. | Горизонтальный круговой цилиндр | Dg | h | — | — | — | 2кm*h-1 | — | |
| Vzx | — | -0,41*h | -0,58*h | +0,58*h | ±1,3кm*h-2 | ||||
| Vzz =VD | ±0,51*h | h | -0,41*h | ±-1,73*h | 2кm*h-2 | -0,25кm*h-2 |
Примечание: h — глубина залегания центра масс;
k — гравитационная постоянная, равная 6,67*10-11 м3/кг*с2;
М=V*Ds =4/3*pR3*Ds (избыточная масса шара);
m=S*Ds = pR2 *Ds (избыточная масса единицы длины цилиндра);
Для горизонтального тонкого пласта обратную задачу можно решить, используя характерные точки по формулам:
 |  |  |
(2.82)
Решение обратной задачи (т.е. определение параметров объекта) обычно выполняют в следующем порядке:
1. Построив графики VZ,VZZ, VZX, по характерным точкам (рис.2.34) определяют глубину до центра объекта (h).
2. Формулы (2.75) или (2.78) записывают для максимального значения VZ (VZmax =VZ при x=0).
3. Сняв с графика значения VZmax и, зная величину h, выражают из полученной формулы избыточную массу М и вычисляют ее.
4. Учитывая, что избыточная масса для сферы определяется, как М=(sоб - sвм)*V, а для горизонтального цилиндра, как М=(sоб - sвм)*S, можно определить объем сферы (V) или площадь сечения (S) цилиндра.
5. Зная V и S , можно по известным формулам объема сферы и площади сечения определить радиус объекта, а затем минимальную глубину бурения (т.е. глубину до верхней точки объекта).
6. Запасы изометричной залежи руды (Р) определяются, как Р=V*sоб, а для цилиндра можно определить запасы единицы его длины, как Р =S*sоб.
7. Расчет относительных погрешностей ведется по формулам:
eh= (çhp - hист.ç/hист.)*100% ,
eр = (çPp - Pист.ç/Pист.)*100% ,
где eh; ep - относительные погрешности определения глубины и запасов объекта соответственно,
hР, hист., PР, Pист. - рассчитанные и истинные значения глубин и запасов.
Дата добавления: 2015-06-27; просмотров: 1355;
