Центр инверсии
Центром инверсии называется такая точка внутри фигуры, при отражении в которой всех точек последняя совмещается сама с собой.
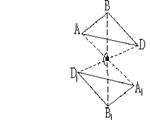
Чтобы произвести отражение какой-либо точки фигуры в центре инверсии (рис. 2.6), нужно соединить эту точку и точку С прямой линией.
Как видно из рис. 2.6 плоскости треугольников параллельны, но стороны имеют противоположные
направления.
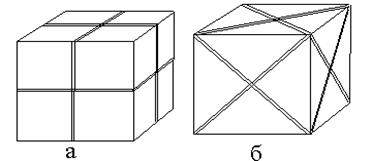
| Рис. 2.5. Куб имеет девять плоскостей симметрии (9Р): три главных плоскости (а) и шесть диагональных (б) |
Центр инверсии называют центром обратного равенства, потому что каждая грань при наличие центра инверсии должна иметь равную себе и обратно параллельную грань (рис. 2.7).
| Рис. 2.6. Треугольник АВD и А1В1D1, связанные центром инверсии, равны друг другу и обратно параллельны |

|
| Рис. 2.7. Многогранник с центром инверсии С: грани попарно равны и обратно параллельны |
| Рис. 2.8. Многогранник не имеет центра инверсии, т.к. для грани q нет парной параллельной грани |
Дата добавления: 2015-06-27; просмотров: 1079;
