Основные свойства кристаллического вещества
Теория решётчатого строения кристаллов была создана в середине 19 века французским кристаллографом О. Бравэ, а затем русский кристаллограф академик Е. С. Фёдоров и немецкий учёный А. Шенфлис завершили математическую разработку этой теории. При создании и разработке теории решетчатого строения кристаллов Бравэ, Фёдоров и др. кристаллографы основывались исключительно на некоторых важных свойствах кристаллического вещества.
Основными свойствами кристаллов являются их однородность, анизотропность, способность самоограняться и симметричность.
Однородным обычно называют тело, которое обнаруживает одинаковые свойства во всех своих частях. Кристаллическое тело однородно, т. к. различные участки его имеют одинаковое строение, т. е. одинаковую ориентировку слагающих частиц, принадлежащих одной и той же пространственной решётке. Однородность кристалла следует отличать от однородности жидкости или газа, которая имеет статистический характер.
Анизотропным называется такое однородное тело, которое обладает неодинаковыми свойствами по непараллельным направлениям. Кристаллическое тело анизотропно, т. к. строение пространственной решётки, а значит и самого кристалла, в общем случае неодинаково по непараллельным направлениям. По параллельным же направлениям частицы слагающие кристалл, как и узлы его пространственной решётки, расположены строго одинаковым образом, поэтому и свойства кристалла по таким направлениям должны быть одними и теми же.
Характерный пример резко выраженной анизотропности представляет слюда, кристаллы которой легко расщепляются лишь по одному определённому направлению. В качестве другого яркого примера анизотропности можно привести минерал дистен (AlOAl[SiO4]), у кристаллов которого боковые грани имеют сильно различающиеся значения твердости в продольном и поперечном направлениях. Если из кристалла каменной соли, имеющего форму куба, вырезать стерженьки по разным направлениям, то для разрыва этих стерженьков потребуются разные усилия. Стерженёк, перпендикулярный граням куба, разорвётся при усилии около 570 Г/мм2; для стерженька, параллельного гранным диагоналям, разрывающее усилие составит 1150 Г/мм2, а разрыв стерженька, параллельного телесной диагонали куба, произойдет при усилии 2150 Г/мм2.
Приведенные примеры, конечно, исключительны по своей характерности. Однако точными исследованиями установлено, что абсолютно все кристаллы в том или ином отношении обладают анизотропностью.
Однородностью и в некоторой степени анизотропностью могут обладать также и аморфные тела. Но ни при каких условиях аморфные вещества не могут сами по себе принимать форму многогранников. Образовываться в виде плоскостных многогранников могут лишь кристаллические тела. В способности самоограняться, т. е. принимать многогранную форму, проявляется наиболее характерный внешний признак кристаллического вещества.
Правильная геометрическая форма кристаллов с давних пор привлекала внимание человека, и её загадочность вызывала в прошлом у людей различные суеверия. Кристаллы таких веществ, как алмаз, изумруд, рубин, сапфир, аметист, топаз, бирюза, гранат и др., ещё в 18 в. считались носителями сверхъестественных сил и использовались не только как драгоценные украшения, но и как талисманы или средство от многих болезней и укусов ядовитых змей.
На самом же деле способность самоограняться, как и первые два свойства, является следствием правильного внутреннего строения кристаллического вещества. Внешние границы кристаллов как бы отражают эту правильность их внутреннего строения, ибо каждый кристалл можно рассматривать как часть его пространственной решётки, ограниченной плоскостями (гранями).
Необходимо вместе с тем отметить, что способность кристаллического вещества самоограняться проявляется не всегда, а только при особо-благоприятных условиях, когда внешняя окружающая среда не мешает образованию и свободному росту кристаллов. При отсутствии таких условий получаются или совершенно неправильные или частично деформированные кристаллы. Несмотря на это они сохраняют все свои внутренние свойства, в том числе и причины, заставляющие кристаллы принимать форму многогранника. Поэтому, если кристаллическое зерно неправильной формы поместить в определённые условия, в которых кристалл сможет свободно расти, то оно примет через некоторое время форму плоскостного многогранника, присущую данному веществу.
Симметрия кристаллов также является отражением их закономерного внутреннего строения. Все кристаллы в той или иной степени симметричны, т. е. состоят из закономерно повторяющихся равных частей, так как их строение выражается пространственной решёткой, которая по своей природе всегда симметрична.
Открытие мюнхенским физиком М. Лауэ в 1912 г. явления дифракции рентгеновских лучей при их прохождении через кристалл явилось первым экспериментальным подтверждением правильности теории решетчатого строения кристаллического вещества. С этого момента стало возможным, с одной стороны, посредством кристаллов исследовать рентгеновские лучи, а с другой - с помощью рентгеновских лучей исследовать внутреннее строение кристаллов. Таким путём было доказано, что абсолютно все кристаллы состоят из частиц, расположенных друг относительно друга закономерно, наподобие узлов пространственной решётки.
После опытов Лауэ теория решетчатого строения кристаллов перестала быть только лишь умозрительным построением и приобрела форму закона.
1.3. Распространённость кристаллических веществ
Неосведомлённому человеку может показаться, что кристаллические тела встречаются в природе очень редко. Действительно, природные монокристаллические образования, имеющие вид плоскостных многогранников, представляют большую редкость. Это, в первую очередь, относится к кристаллам большой величины, размеры которых в отдельных случаях могут достигать человеческого роста. Таковы гигантские кристаллы кварца и гипса, хранящиеся в Московском минералогическом музее АН России и в Горном музее Санкт-Петербургского горного института. В 1958 г. в Средней Азии был найден уникальный кристалл кварца весом около 30 т., длиной 7,5 м. и шириной 1,6 м.
Разумеется, описанные случаи относятся к числу выдающихся. Обычно же приходится иметь дело с гораздо более мелкими и нередко микроскопическими кристалликами.
В наиболее общем случае кристаллизация происходит из многих центров одновременно, поэтому отдельные кристаллы в процессе своего роста приходят в соприкосновение друг с другом и не могут приобрести геометрически правильную огранку. В результате образуются поликристаллические тела, состоящие из множества кристаллических зёрен с криволинейными очертаниями, которые часто называют “кристаллитами”. Тем не менее, как было установленно рентгеноскопическими исследованиями, кристаллиты обладают таким же закономерным внутренним строением, что и кристаллические многогранники.
Из подобных кристаллических зёрен различной крупности, от видимых простым глазом до не различимых даже под микроскопом, состоят, например, металлы и сплавы, кирпич и бетон, твёрдые шлаки и минеральные удобрения, самые разнообразные продукты химической и пищевой промышленности. То же самое можно сказать и о подавляющем большинстве горных пород, слагающих земную кору, которые образовались из застывающей магмы (граниты, базальты, диориты, перидотиты и др.), кристаллическими являются также руды железа и цветных металлов и осадочные породы органогенного и химического происхождения - известняки, доломиты, гипс, каменная соль и т. п. Из мельчайших обломков кристаллов состоят и такие распространенные механические осадки, как песок, глина и алеврит. Кристаллические вещества принимают участие даже в строении органического мира. Например, роговица глаза, зубы, некоторые кости скелета, пчелиный воск - представляют собой агрегаты мельчайших кристалликов, не обнаруживаемых с помощью обычных микроскопов.
Благодаря применению рентгеновских лучей и электронных микроскопов круг известных нам кристаллических веществ всё более расширяется. Имеющиеся данные достаточно убедительно свидетельствуют о чрезвычайной распространённости кристаллов в природе. Образно выражаясь, мы живем в мире кристаллов, ибо кристаллы окружают нас всюду.
1.4. Пространственная решётка
Познакомимся теперь подробнее с построением и некоторыми свойствами пространственной решётки.
Примем какой-либо узел пространственной решётки, например, узел А0, за исходный узел решётки (рис. 1.1). Пусть ближайший к нему такой же атом (узел) А1 находится на расстоянии а (а --> А0А1). Продолжив прямую А0А1, найдем серию узлов А2,А3, А4, . . . , Аn, расположенных вдоль этой прямой на равном расстоянии друг от друга.
Совокупность узлов, лежащих на одной прямой, называется рядом пространственной решётки.
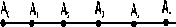
|
| Рис. 1.1. Ряд пространственной решётки |
Расстояние между соседними узлами ряда называется промежутком ряда. В нашем случае промежуток ряда равен а.
Число узлов, приходящихся на единицу длины ряда, называется плотностью ряда. Очевидно, что плотность ряда обратно пропорциональна величине промежутка: чем меньше промежуток ряда, тем больше будет его плотность.
Одно из основных свойств пространственной решётки состоит в том, что через любой узел решётки всегда можно провести ряд, параллельный данному ряду, причём все параллельные ряды имеют одинаковую плотность. Ряды же разных направлений в общем случае обладают различной плотностью. В частных случаях и у непараллельных рядов промежутки могут быть одинаковыми.
Возьмём теперь относительно исходного узла А0 ещё один ближний к нему узел, лежащий в плоскости чертежа, но не вне ряда А0Аn. Пусть это будет узел В1, отстоящий от узла А0 на расстояние b (рис. 1.2). Соединив узлы А0 и В1 прямой линией и продолжив её дальше, получим новый ряд А0Вn с промежутком ряда b.
Два пересекающихся ряда А0Аn и А0Вn, определяют положение плоскости, которая пройдёт через бесконечное множество узлов пространственной решётки.
Совокупность узлов пространственной решётки, лежащих в одной плоскости, называется плоской сеткой.
Узлы всякой плоской сетки можно расположить в вершинах равных и параллельных друг другу параллелограммов, смежных по целым сторонам. Такую систему параллелограммов в нашем случае получим, если через узлы В1, В2, . . . , Вn проведём ряды, параллельные ряду А0Аn, а через узлы А2.,А3,А4, . . . ,Аn, - ряды, параллельные ряду А0Вn (см. рис. 2) .
Число узлов, приходящихся на единицу площади плоской сетки, называется её ретикулярной плотностью.
Согласно второму основному свойству пространственной решётки через любой узел решётки можно провести плоскую сетку, параллельную данной и имеющую такую же ретикулярную плотность. Таким образом в решётке параллельно каждой плоской сетке проходит бесконечное множество тождественных плоских сеток. Совокупность параллельных друг другу плоских сеток пространственной решётки будем называть серией плоских сеток. Расстояние между двумя ближайшими параллельными плоскими сетками называется межплоскостным расстоянием.

| Рис. 1.2. Плоская сетка |
В пространственной решётке имеется бесчисленное множество различным образом ориентированных плоских сеток, поскольку через три любых узла решётки всегда можно провести плоскую сетку.
Непараллельные плоские сетки отличаются друг от друга не только положением в пространстве, но в общем случае и ретикулярной плотностью.
Для дальнейшего построения пространственной решётки возьмём относительно исходного узла А0 ближайший к нему узел С1, не лежащий в плоскости построенной нами плоской сетки Аn-А0-Вn (рис. 3). Проведя прямую А0С1 и продолжив её, найдём на ней серии узлов С2,С3, . . . ,Сn, образующих третий ряд А0Сn, непараллельный первым двум и имеющий промежуток с.
Через каждый узел этого ряда проведём плоские сетки, параллельные сетке Аn-A0-Bn. Все они в совокупности образуют серию плоских сеток. Вторую серию плоских сеток получим, если через все узлы ряда А0Аn провести плоские сетки, параллельные оси Вn-A0-Cn, определяемой пересекающимися рядами А0Вn и А0Сn. Наконец, можно построить третью серию плоских сеток, проведя через узлы ряда А0Вn плоские сетки, параллельные сетке Аn-A0-Cn, определяемой рядами А0Аn и А0Сn.
Три серии построенных плоских сеток, взаимно пересекаясь, образуют систему равных, параллельно ориентированных и смежных по целым граням параллелепипедов, т. е. пространственную решётку. На рис.1.3 один из параллелепипедов решётки выделен жирными линиями. Все узлы полученной решётки располагаются только в вершинах параллелепипедов. Если известно расположение узлов решётки у одного параллелепипеда, то можно построить всю решётку параллельным повторением данного, поступательно перемещая параллелепипед на величину его рёбер по их направлению.

| Рис.1. 3. Пространственная решётка |
Параллелепипед, поступательным перемещением которого на величину и по направлению его рёбер можно построить всю пространственную решётку, называется параллелепипедом повторяемости.
Параллелепипеды повторяемости можно выделить у данной пространственной решётки самым различным образом (рис. 1.4).
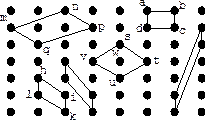
|
| Рис. 1.4. Различные параллелепипеды повторяемости пространственной решётки (на чертеже показаны только основания параллелепипедов) |
В одних случаях параллелепипеды повторяемости могут не иметь никаких других узлов, кроме узлов в вершинах (например, параллелепипеды abcd и hikl).В других же случаях параллелепипеды повторяемости, помимо узлов в вершинах, могут заключать узлы ещё и внутри себя или на своих гранях (например, параллелепипеды mnpq и stuv). Вершины подобных параллелепипедов не образуют всех узлов данной пространственной решётки. Параллелепипеды повторяемости, имеющие узлы только в своих вершинах, называются примитивными. Вершины примитивных параллелепипедов образуют все узлы данной пространственной решётки.
Если узлы решётки располагаются только в вершинах параллелепипедов повторяемости, то каждый узел принадлежит одновременно восьми попарно смежным параллелепипедам (рис. 1.3). Следовательно, на долю одного параллелепипеда приходится 1/8 узла, находящегося в его вершине. Поэтому на один примитивный параллелепипед приходится всего 1/8 × 8 = 1 узел пространственной решётки.
Одна и та же пространственная решётка может быть разбита на примитивные параллелепипеды различными способами, но каким бы способом мы ни разбивали нашу решётку на параллелепипеды, её общий объём и количество узлов остаются неизменными. А так как каждому узлу отвечает всегда один примитивный параллелепипед, то любые примитивные параллелепипеды данной пространственной решётки имеют одинаковый объём. У всех других параллелепипедов повторяемости, не являющихся примитивными, объём будет больше, так как количество узлов, приходящихся на непримитивный параллелепипед, всегда превышает 1.
Построенная нами пространственная решётка представляет собой бесконечную фигуру, поскольку каждый из рядов решётки может быть продолжен неопределённо далеко.
Реальные кристаллы являются телами конечных размеров, поэтому, как уже отмечалось выше, их можно рассматривать как части пространственных решёток, ограниченные плоскостями - гранями. С точки зрения учения о пространственной решётке грани кристалла представляют собой плоские сетки, а рёбра - ряды его решётки.
Необходимо при этом иметь в виду, что реальные кристаллические вещества часто образуют сложные решётки, состоящие из двух или нескольких геометрически равных простых пространственных решёток, определённым образом вставленных друг в друга. Такие сложные решётки получили название кристаллических решёток. Узлами кристаллических решёток являются всегда только атомы или ионы химических элементов.
На рис. 1.5 приведены кристаллические решётки некоторых элементов.
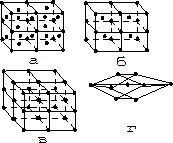
|
| Рис. 1.5.Кристаллические решетки меди(а), хлористого цезия (б), хлористого натрия(в) и кальцита(г) |
Кристаллическая решётка хлористого цезия (рис. 1.5 б) состоит из двух простых решёток, одна из которых имеет узлы, соответствующие ионам цезия, а другая - совпадающие с ионами хлора. Обе решётки совершенно тождественны и сдвинуты друг относительно друга на величину расстояния между ионами Cs+ и Cl- так, что вершины параллелепипедов одной решётки находятся в центрах параллелепипедов другой решётки.
Кристаллическую решётку хлористого цезия можно всегда заменить простой пространственной решёткой, примитивным параллелепипедом которой будет являться ромбоэдр.
Решётка кристаллов хлористого натрия (каменной соли) состоит из двух одинаковых решёток, подобных кристаллической решётке меди (рис. 1.5 а). При этом решётка, отвечающая ионам натрия, так вставлена в решётку, соответствующую ионам хлора, что узлы натриевой решётки занимают середину ребра параллелепипедов повторяемости хлорной решётки и наоборот.
Кристаллическая решётка кальцита состоит из двух одинаковых решёток, одна из которых отвечает катионам кальция, а другая - анионам СО32-. Параллелепипед повторяемости этих решёток имеет форму ромбоэдра с узлами в вершинах и в центре параллелепипеда (рис. 1.5 г).
Всякий атом или ион представляет собой весьма сложную систему, состоящую из положительно заряженного ядра и отрицательно заряженных электронных оболочек. Поэтому между атомами и ионами действуют как силы притяжения, так и силы отталкивания.
В грубой схеме два соседних атома (или иона) будут притягиваться друг к другу до тех пор, пока силы притяжения не будут уравновешены силами отталкивания. А так как атомы (ионы) различных химических элементов имеют различное строение, то неодинаковы и силы их взаимодействия. Следовательно, и расстояния между атомами (ионами) различных химических элементов в кристаллической решётке должны быть разными.
Вот почему вещества различного химического состава имеют различные кристаллические решётки. Это - основной закон о кристаллических решётках, на котором базируется вся кристаллохимия.
Дата добавления: 2015-06-27; просмотров: 2341;
