Прямые и обратные задачи гравиразведки

Основой интерпретации данных гравиразведки является решение прямых и об- ратных задач. Прямая задача гравиразведки состоит в определении элементов поля си- лы тяжести (Δg, WXZ, WYZ и т. д.) по заданному распределению его источников, когда известны форма, размеры, глубина залегания и величина избыточной плотности. Об- ратная задача гравиразведки ставит противоположную цель — нахождение параметров объекта (формы, размеров, глубины залегания, избыточной плотности) по известному распределению (на профиле или на площади) элементов силы тяжести.

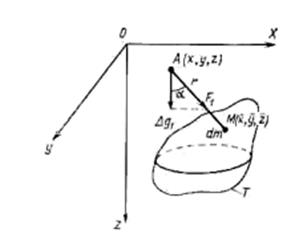
кона Ньютона). Для этого гравитирующее тело разбивают на элементарные массы dm; рассчитывают аномалию такой точеч- ной массы Δg1, которая равна вертикаль- ной составляющей силы ньютоновского притяжения F1 этой массой массы 1 г, на- ходящейся в точке наблюдения А, т. е. бе- рут составляющую силы притяжения по направлению действия силы тяжести Зем- ли g; наконец, используя принцип супер- позиции, определяют аномалию за счет притяжения всем телом ΔgT, как сумму

притяжении всех элементарных точечных

масс, которыми можно представить ано-

малообразующее тело (рис.2.5).

Математически сказанное можно за-

писать так. Согласно выражению (2.1)

Рис.2.5. Схема определения аномалий си-

лы тяжести от элементарной мас-

сы dm и гравитирующего тела Т

_

-

Dg = F × cos a = G × dm × ( z - z ) / r 2 ,

где

cosa = ( z - z ) / r ,

r = ( x - x )2 + ( y - y )2 + ( z - z )2 - расстояние между

точкой наблюдения А (х, у, z) и точкой

M( x,y ,z ) , в которой находится элементарная

точечная масса. В природных условиях аномальные включения с плотностью σ нахо- дятся во вмещающей среде с плотностью σ0, поэтому под массой dm надо понимать из- быточную массу dm=(σ — σ0)dV =Δσ dV, где dV—элементарный объем точечной массы; Δσ — избыточная плотность. Поэтому окончательные выражения для расчета

аномалии силы тяжести точечной массы и тела, используемые в теории гравиразведки,

имеют вид

D s ( z - z )dV

. (2.26)

3

V [( x -x )2 +( y -y )2 +( z -z )2 ] 2

Интеграл в последней формуле берут по всему объему тела V. При σ > σ0 ΔgT имеет положительный знак, т. е. наблюдаются увеличение притяжения и положитель- ные аномалии. При σ < σ0 ΔgT имеет отрицательный знак, т. е. наблюдаются умень- шение притяжения и отрицательные аномалии.

Аналитические решения с помощью уравнения (2.26) получаются лишь для тел простой геометрической формы (шар, цилиндр и др.) с постоянной избыточной плот- ностью. Для тел более сложной формы, а особенно с переменной плотностью, возмож- ны лишь численные решения интеграла (2.26) с помощью ЭВМ. Анализ решений пря- мых задач служит основой при разработке приемов решения обратных задач гравираз- ведки для типовых геологических структур и объектов. Рассмотрим несколько приме- ров решения прямых и обратных задач для тел правильной геометрической формы.

Прямая и обратная задачи для шара. Пусть однородный шар радиусом R, объе- мом V, с избыточной плотностью Δσ расположен на оси Z на глубине h (рис.2.6, а). Ре- шим прямую задачу, т. е. определим гравитационный эффект вдоль наземного профиля ОХ, проходящего через проекцию центра шара с началом координат над ним (см. рис.2.6). Поскольку по закону всемирного тяготения шар притягивается с такой же си- лой, как точечная масса, сосредоточенная в его центре, аномалию над шаром Δgш мож- но получить без решения интеграла (2.26), считая, что аномалия силы тяжести над ша- ром и аномалия точечной массы, помещенной в его центре, совпадают:

= G × M × h /( x2

3

+h2 ) 2

(2.27)

где M= Δσ V —избыточная масса шара. График Δgш будет иметь максимум над цен- тром шара Δgmax=GM/h2 (при х=0) и асимптотически стремиться к нулю при х → ± ∞ (см. рис.2.6, а). Знак Δgш определяется знаком Δσ. Формула для второй производной потенциала или горизонтального градиента силы тяжести получает вид

) =-3GMhx .

(2.28)

XZ ¶x

¶x r 5

График WXZ имеет перед шаром максимум (х<0), а за шаром — минимум (x>0). Над центром шара WXZ=0 (см. рис.2.6, а). Если провести расчеты, например, Δgш по ряду профилей, то очевидно, что карта аномалий Δgш будет иметь вид концентриче- ских окружностей с центром над шаром.

Из анализа уравнения (2.27) и графиков на рис.2.6, а, можно решить обратную за-

дачу. Например, найдем абсциссу x1/2, в которой Δgш достигает половины максимума:

( x2

GMh

3

+h2 ) 2

=GM ,

2h2

1 2

откуда (x21/2+h2)3/2=(1/2)h3. Решив это уравнение, получим

|x1/2| =0,76 h или h = 1,31 |x1/2|. (2.29)

Таким образом, определив по графику Δgш значения Δgmax, 1/2 Δgmax и абсциссу точки кривой x1/2, где Δgш= 1/2 Δgmax, и умножив ее на коэффициент 1,31, можно опре- делить глубину залегания центра шарообразной залежи h. Далее можно рассчитать из-

быточную массу M = Δgmaxh2/G, а зная Δσ – объем шара V=MΔσ, радиус. R, а также глубины залегания верхней hВ=h - R и нижней hН=h + R кромок.

Прямая и обратная задачи для горизонтального кругового цилиндра. Пусть го- ризонтальный бесконечно длинный круговой цилиндр радиуса R, сечения s, с избыточ- ной плотностью Δσ расположен вдоль оси Y на глубине h (рис.2.6, б). Решим прямую задачу, т. е. определим ΔgГЦ и WXZ вдоль оси X, направленной вкрест простирания ци- линдра с началом координат над его центром. Притяжение цилиндром будет таким же, как притяжение вещественной линии, расположенной вдоль его оси с массой единицы длины dm = πR2Δσdy. Поэтому для точек наблюдения вдоль оси X (y=z=0) с учетом, что х=0, - ∞< y < ∞ (цилиндр считается бесконечно длинным), z=h, аналитическое

выражение можно получить из уравнения (2.26):

Dg Г .Ц .

=GDsR 2

2

dy

2 2 3

=2GM 1h ,

x 2 +h 2

(2.30)

-¥( x +y

+h ) 2

где М1=πR2Δσ — избыточная масса единицы длины цилиндра.

График ΔgГЦ будет иметь максимум Δgmax= 2GM1/h (при х=0) и, как и Δgш, асимптотически стремиться к нулю при х → ± ∞. Очевидно, что в плане изолинии ΔgГЦ будут представлять систему параллельных оси цилиндра линий. В целом график ΔgГЦ и WXZ вдоль оси X будет примерно таким же, как и над шаром.

Решим обратную задачу для горизонтального бесконечно длинного кругового ци-

линдра тем же приемом, что и для шара:

) = GM 1 / h,

(2.31)

= x 2 + h2 ,

h =| x1 2 | .

Таким образом, определив по графику ΔgГЦ значение Δgmax, ½ Δgmax и абсциссу

x1/2, можно получить глубину залегания оси цилиндра h, далее рассчитать единичную

избыточную массу M1 = Δgmaxh /2G, а зная Δσ, определить площадь поперечного сече- ния цилиндра s=πR2=M1/Δσ, его радиус R, а также глубину залегания верхней hв= h-R и нижней hн=h+R кромок.

Прямая и обратная задачи для вертикального уступа. Под вертикальным ус- тупом в теории интерпретации гравитационных аномалий понимают горизонтальный полупласт, ограниченный вертикальной гранью, бесконечного простирания по оси Y (рис.2.7). Плотность пород уступа и вмещающих пород различна и составляет постоян- ную и отличную от нуля величину Δσ. Если глубину верхней горизонтальной плоско- сти, ограничивающей полупласт, обозначить h1, нижней — h2, а боковую вертикаль- ную грань совместить с осью Z, то гравитационное поле Δgуст в точках x (вдоль оси Х при z=0 и y=0) соответствует выражению (2.26) при определенных пределах интегри- рования:

Dg ( x ) =GDsp

¥ +¥ h2

z d x d y d z

± =

уст

ò ò ò

2 2 2 3

0

ì 2 2

-¥h1 [( x -x ) +y

+z ] 2

(2.32)

ü

+h2

2

-h1

) +2h2 arctg

x x

-2h1 arctg ý.

î x +h1

h2 h1 þ

Вид кривой Δgуст (при σ > σ0) приведен на рис.2.7. При х → ± ∞ значения Δg вы- ходят на горизонтальные асимптоты с максимальной аномалией Δgmax=2πGΔσΔh. Над самим вертикальным сбросом (при х=0) получаем Δg = (1/2) Δgmax= πGΔσΔh. Оче- видно, на карте Δgуст будут наблюдаться параллельные изолинии с максимальным сгущением изолиний над вертикальной гранью. Из выражения (2.32) можно получить для абсцисс точек с x1/4 и x3/4, в которых Δgуст составляет 1/4 и 3/4 от Δgmax, выраже- ние для определения средней глубины залегания вертикального уступа

hср= (h1+h2)/ 2 = x1/4 = x3/4

Если известна избыточная плотность Δσ, то можно определить мощность сброса

Δh= Δgmax/2πGΔσ и рассчитать глубину залегания верхней h1= hcp - Δh /2 и нижней h2

= hcp + Δh /2 кромок.

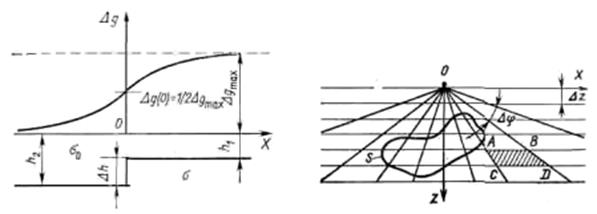
Рис.2.7 Гравитационное поле над верти-

кальным уступом (сбросом)

Рис.2.8. Палетка Гамбурцева для вычисления притяжения двумерными телами с контуром сечения двумерного тела S

Палеточный способ решения прямых задач гравиразведки. Для вытянутых тел сложного сечения и постоянной избыточной плотности расчет Δg можно проводить с помощью палетки Гамбурцева. Палетка приведена на рис.2.8. Здесь из точки О через один и тот же угол Δφ проведены радиусы, а через равные расстояния Δz — параллель-

ные линии. Оказывается, что значения силы тяжести Δg в точке О за счет притяжения одной бесконечной по оси Y горизонтальной призмой сечением в виде трапеции ABCD одинаково для любой из таких призм и Δgп=2GΔσпΔφΔz. Если на поперечное сечение исследуемого тела приходится т таких элементарных трапеций палетки, то Δg(0)=m·Δgп. Параметр Δgп представляет собой цену деления палетки и определяется заранее по заданным параметрам разреза, причем Δφ и Δz подбирают так, чтобы цена деления имела какое-либо удобное для расчета постоянное значение, например, 0,1 мГал.

При переходе с одного разреза на другой могут измениться масштаб (и, следова- тельно, Δz на палетке) и значение избыточной плотности. Чтобы воспользоваться этой же палеткой, необходимо ввести масштабный коэффициент

Ds M

k = р × п ,

где Δσп, Мп—избыточная плотность и масштаб палетки, а Δσр, Мр — избыточная плот- ность и масштаб разреза. Таким образом, аномалию над двумерным телом с помощью палетки Гамбурцева рассчитывают по формуле

Δg = m Δgп k (2.33)

Точность расчета Δg палеточным методом зависит от точности аппроксимации поперечного сечения плотностных масс элементарными ячейками палетки и может быть повышена путем уменьшения цены деления палетки. Существуют и другие пале- точные способы решения прямых задач гравиразведки, в том числе и трехмерных.

Численные методы решения прямых задач гравиразведки Для более сложных форм аномальных объектов с изменяющейся избыточной плотностью при решении прямой задачи гравиразведки применяют численные методы решения прямых задач гравиразведки. Для этого по заданному распределению масс получают значения эле- ментов гравитационного поля, например, с помощью способов механических кубатур. Суть такого подхода — в замене реального объекта суммой n объектов простой гео- метрической формы и постоянной плотности. Гравитационный эффект Δgi от каждого i-го элементарного объема рассчитывают по формуле (2.30), а значение Δg(x) в каждой точке определяют как их сумму

n

Dg( x ) =å Dgi .

i =1

Метод требует разбиения объекта на достаточно большое число ячеек, использо- вания сложных, но повторяющихся в расчетах специфических выражений и поэтому относительно просто реализуется с помощью современных ЭВМ. Погрешность чис- ленного метода решения составляет 1—5 %.

Основные выводы из анализа решений прямых задач гравиразведки. Анализ ре-

шения прямых задач гравиразведки позволяет сделать следующие выводы.

1. Знак аномалии Δg определяется знаком избыточной плотности и над относи- тельно «легкими» (Δσ < 0) объектами фиксируются отрицательные аномалии, а над более плотными (Δσ > 0 ) — положительные.

2. Экстремальные значения Δgmax наблюдаются над центрами тяжести этих объ- ектов, а их интенсивность прямо пропорциональна избыточной плотности и обратно пропорциональна для вытянутых тел глубине, а для изометричных тел - квадрату глу- бины.

3. Форма аномалий Буге ( ΔgБ ) на картах и графиках тесно связана с пространст- венным положением избыточных масс: под вытянутыми (двумерными) аномалиями залегают вытянутые структуры или геологические тела, под изометричными — округ- лые в плане объекты.

4. Существует аналитическая или статистическая связь между абсциссами харак- терных точек на кривых ΔgБ и глубинами залегания гравитирующих тел, что позволяет, аппроксимируя их телами простых геометрических форм, решать обратную задачу гра- виразведки. При этом некоторые параметры, например h, рассчитывают достаточно однозначно. Для определения других параметров, например V, s, требуется привлече- ние дополнительных данных (избыточной плотности).

5. Чем глубже залегает тот или иной гравитирующий объект, тем более широкую и расплывчатую (региональную) аномалию создает он на земной поверхности (эффект дальнодействия).