Турбины ТЭС и АЭС
Саратов
Решетки профилей осевых турбин
Основным типом турбин в настоящее время являются осевые турбины. Основным элементом турбины, в котором происходит преобразование энергий потока пара или газа, является проточная часть.
Проточная часть состоит из неподвижных и подвижных решеток профилей.
К неподвижным решеткам профилей относятся сопловая решетка и направляющая решетка (для турбин с венцами скорости); к подвижным – рабочая решетка.
Геометрические и режимные характеристики решеток.
Обозначения основных величин
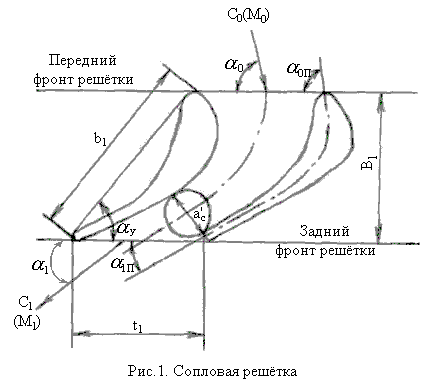
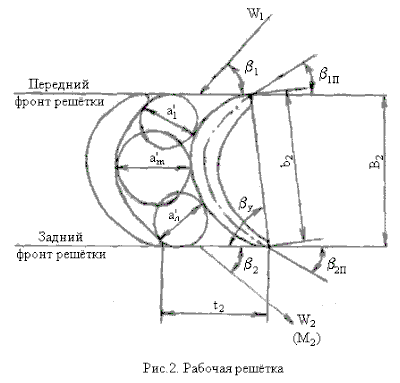
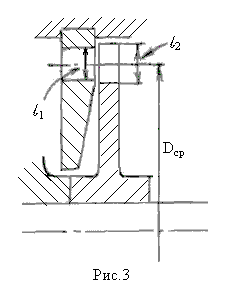
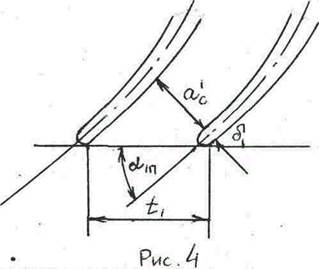
Кромки профиля со стороны набегания потока именуются входными кромками, а со стороны выхода потока – выходными. Линия, касательная к входным кромкам называется линией переднего фронта, а касательная к выходным кромкам – линией заднего фронта. Основные геометрические и режимные характеристики показаны на рис. 1, 2, 3 и 4.
 |  | ||
Геометрические характеристики решетки
В – ширина решетки (расстояние между линиями переднего и заднего фронта),
t – шаг решетки,
b – хорда профиля (расстояние между перпендикулярами к линии, касательной к входной и выходной кромкам профиля, как бы "зажимающими" профиль)
a’c; a’л – ширина канала на выходе,
С- высота решетки в выходном сечении,
d – толщина выходной кромки профиля,
Dср – средний диаметр облопатывания решетки,
t – коэффициент загромождения выходного сечения кромками профилей,
ay, by – угол установки профиля (угол между хордой профиля и линией заднего фронта),
a0П, b1П – геометрические углы входных кромок профиля (геометрические входные углы),
a1П, b2П – геометрические выходные углы.
Геометрические углы профиля – это углы междулиниями фронта решетки и касательными к базовой линии профиля на входной и выходной кромках.
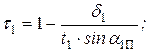

Относительные геометрические характеристики
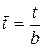 – относительный шаг решетки, 6
– относительный шаг решетки, 6
 – относительная высота решетки.
– относительная высота решетки.
Режимные характеристики решеток
С0 и С1 – абсолютные скорости потока при входе на сопловую решетку и при выходе из неё,
W1 и W2 – относительные скорости потока при входе на рабочую решетку и при выходе из неё,
a0 и b1 – углы входа потока, соответственно, на сопловую и рабочую решетки,
a1 и b2 – соответствующие углы выхода
a1эф и b2эф – эффективные углы выхода, соответственно, с сопловой и рабочей решеток,
М1 и М2 – число Маха в выходном сечении решетки
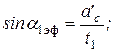
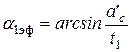
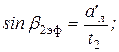
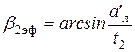
 и
и 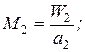 где а1; a2 – скорость звука при параметрах в выходном сечении.
где а1; a2 – скорость звука при параметрах в выходном сечении.
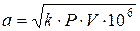 м/сек; здесь К – показатель адиабаты расширения;
м/сек; здесь К – показатель адиабаты расширения;
для перегретого водяного пара К = 1,3
для воздуха К = 1,4
для влажного водяного пара. К = 1,035 + 0,1×Х
Р – МПа, давление в выходном сечении; V – м3/кг – удельный объем там же.
| Классификация решеток профилей | |
| Все применяемые в турбостроении решетки можно разделить на группы в зависимости от числа Маха в выходном сечении решетки: | |
| дозвуковые при М < 0,9 | - группа А |
| околозвуковые 0,9 < М < 1,2 | - группа Б |
| сверхзвуковые М > 1,2 | - группа В |
Основные уравнения, описывающие процессы преобразования энергии в турбине
Процессы преобразования тепловой энергии пара (газа) в механическую энергию вращения ротора турбины связаны с течением потока через каналы решеток профилей.
Экономичность преобразования энергии, а следовательно и КПД турбины, зависит от того, насколько совершенным будет течение потока, насколько малы в нем потери.
Таким образом, в основе процессов, имеющих место в проточной части турбины, лежат законы истечения и их основные уравнения, а также термодинамические зависимости, касающиеся свойств паров и газов. К их числу можно отнести:
1. Уравнения закона сохранения энергии
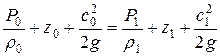
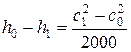 Здесь h0 и h1 начальная и конечная энтальпия потока, кДж/кг
Здесь h0 и h1 начальная и конечная энтальпия потока, кДж/кг
с0 и с1 – соответствующие скорости, м/с.
2. Уравнение сплошности
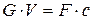 Здесь G – массовый расход, кг/с,
Здесь G – массовый расход, кг/с,
V – удельный объем вещества в расчетном сечении, м3/кг,
F – площадь расчетного сечения, м2,
с – осредненная скорость потока в расчетном сечении, м/с.
3. Уравнение количества движения
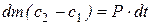 где dm – массовый расход за какой-то промежуток времени, кг
где dm – массовый расход за какой-то промежуток времени, кг
c1 и c2 – начальная и конечная скорости,м/с,
P – сила, действующая на поток, н,
dt – промежуток времени действия силы, сек.
4. Уравнения состояния рабочего вещества (водяного пара, паров других рабочих веществ, воздуха, продуктов сгорания и др.) на базе которых построена соответствующие диаграммы (h-s и др.).
При решении большинства практических задач принимается, что поток рабочего вещества в каналах решеток профилей турбины является установившимся.
Преобразование энергии потока в соплах
В курсе "Газовая динамика" были рассмотрены основные вопросы теории истечения паров и газов из сопел. Полученные результаты сводятся в основном к следующему:
а). применяются два типа сопел
1. сходящиеся – с наименьшим сечением на выходе,
2. расходящиеся (Лаваля) с наименьшим сечением внутри канала, за которым идет конус расширения.
б). основным критерием для классификации возможных случаев применения сопел является так называемое "критическое отношение давлений", при котором расход через сопло достигает максимума.
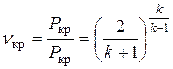
Если 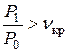 , т.е. при малом перепаде давлений, применяются сходящиеся сопла; с1.< а.
, т.е. при малом перепаде давлений, применяются сходящиеся сопла; с1.< а.
При 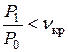 но если эти значения близки – сходящиеся сопла с расширением в косом срезе; с1 > a.
но если эти значения близки – сходящиеся сопла с расширением в косом срезе; с1 > a.
При 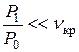 – расходящиеся сопла;с1 > a.
– расходящиеся сопла;с1 > a.
Теоретическая скоростьистечения из сопла в любом случае может быть найдена из уравнения закона сохранения энергии
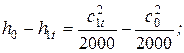
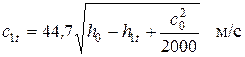
при c1t >> c0 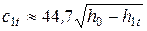
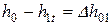
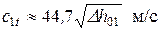
Действительный процесс истечения
При действительном процессе истечения часть располагаемой энергии потока расходуется на преодоление вредных сопротивлений.
Потерянная кинетическая энергия превращается в работу по преодолению сопротивлений, главным образом на преодоление сил трения, которая, в свою очередь, превращается в тепловую энергию повышающую энтальпию протекающего потока.
Таким образом, действительный процесс истечения при том же перепаде давлений является не адиабатным, а политропным.
Фактическая скорость истечения из соплового аппарата будет меньше теоретической: c1 < c1t, а конечная энтальпия потока – больше теоретической: h1 > h1t.
c1 = jc1t, где j < 1 – коэффициент, учитывающий потерю скорости в соплах.
Общее уравнение сохранения энергии одинаково справедливо как для случая идеального истечения без потерь энергии, так и для реального течения, сопровождающегося потерями.
Для адиабатного расширения 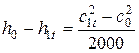
Для политропного расширения 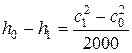
Если из левой части первого уравнения вычесть левую часть второго, то получим потерю (недоиспользование) энергии в сопловой решетке Dhс.
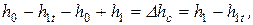 т.е.
т.е. 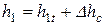
Проделав аналогичную операцию с правыми частями, получим величину потери энергии через скорости потока:
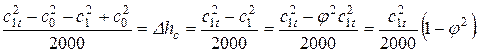
Левая часть уравнения сохранения энергии для идеального истечения соответствует располагаемому (адиабатному) теплоперепаду на сопловой решетке 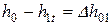 .
.
При очень большой разности в скоростях с1t и c0 (с1t >> c0),что практически всегда имеет место, величиной 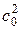 можно пренебречь.
можно пренебречь.
Из уравнения сохранения энергии получаем
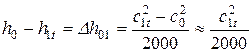
Тогда 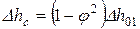 .
.
Наряду с коэффициентом потери скорости j вводится коэффициент потери энергии в сопловой решетке xс.
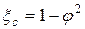 или
или 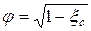
Тогда 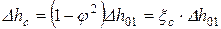
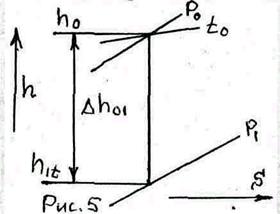
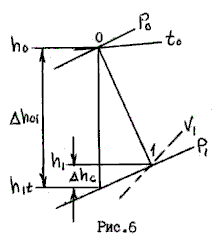 Построение действительного процесса расширения потока в сопловой решетке показано на рис. 6.
Построение действительного процесса расширения потока в сопловой решетке показано на рис. 6.
Состояние пара (газа) в конце действительного процесса расширения на тепловой диаграмме определяется точкой 1.
Дата добавления: 2015-06-27; просмотров: 1359;
