Морении
Метод гониометрического определения кристаллического вещества и в известной степени его внутреннего строения по внешним формам кристаллов позволили Федорову ввести в практику диагностики минералов кристаллохими ч е с к и й анализ.
соотношения его III
Открытие закона постоянства углов позволило измерением гранных углов кристаллов и сравнением данных измерения с имеющимися табличными величинами устанавливать принадлежность исследуемого кристалла к определенному веществу. Федоров провел большую работу по систематизации огромного литературного материала но измерению кристаллов. Использовав его, а также собственные измерения кристаллов. Федоров написал монографию «Царство кристаллов» (1920).
Ученики и последователи Федорова —советский кристаллограф А. К. Болдырев, английский ученый Т. Бар-кер (1881 — 1931) значительно упростили методы определения кристаллов. В настоящее .время кристаллохимический анализ сводится к измерению на гониометре необходимых углов и к определению вещества по справочным таблицам .
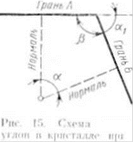
При гониометрическом измерении кристаллов непосредственному определению подлежит внутренний угол между гранями (рис. 15, А\>,). Однако в сводных таблицах с измеренными углами различных веществ всегда приводится угол, составленный нормалями к соответствующим граням (рис. 15, ї(1).Поэтому после- измерения следует произвести несложные вычисления по формуле о=180°- |5 (а=аь как углы с взаимно перпендикулярными сторонами) и по справочнику определить название минерала.
Симметрия вкристаллах
О существовании симметрии в природе мы узнаем с раннего детства. Крылья бабочки и стрекозы, лепестки и листья различных цветов и растений, снежинки и птицы убеждают нас в том, что в природе существует симметрия.
Симметричными называются тела, состоящие из одинаковых, симметричных частей, которые могут совмещаться. Так, если бабочка сложит крылья, они у нее полностью совместятся. Плоскость, которая разделит бабочку на две части, будет плоскостью симметрии. Если на место этой плоскости поставить зеркало, то в нем мы увидим симметричное отражение другого крыла бабочки. Так н плоскость симметрии обладает свойством зеркальности — по обе стороны этой плоскости мы видим симметричные, зеркально-равные половинки тела.
В результате изучения кристаллических форм минералов выяснено, что и в неживой природе, в мире кристаллов, существует симметрия. В отличие от симметрии в живой природе она называется кристаллической симметрией.
Кристаллической симметрией называется правильная повторяемость элементов ограничения (ребер, граней, углов) и других свойств кристаллов по определенным направлениям.
Наиболее отчетливо симметрия кристаллов обнаруживается в их геометрической форме. Закономерное повторение геометрических форм можно заметить, если: 1) рассечь кристалл плоскостью; 2) вращать сто вокруг определенной оси; 3) сопоставить расположение элементов ограничения кристалла относительно точки, лежащей внутри его.
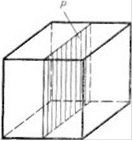
Плоскость симметрии. Рассечем кристалл каменной |Јоли иа две половины (рис. 16). Проведенная плоскость «разделила кристалл на симметричные части. Такая плос-' кость называется плоскостью симметрии.
Плоскостью симметрии кристаллического многогранника называется плоскость, по обе стороны которой располагаю! ся одинаковые элементы ограничения и повторяются одинаковые свойства кристалла.
Рис. 16. Плоскость симметрии (Р) в кристалле каменной соли
І і____ 4/:.
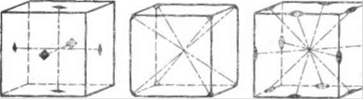
Рис. 17. Плоскости симметрии в кубе
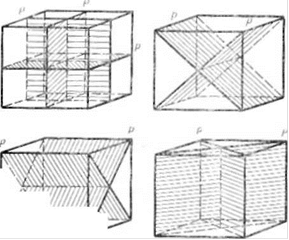
Плоскость симметрии обладает свойством зеркальности: каждая из частей кристалла, рассеченного плоскостью симметрии, совмещается с другой, т. е. является как бы ее зеркальным изображением. В различных кристаллах можно провести разное количество плоскостей симметрии. Например, в кубе имеется девять плоскостей симметрии (рис. 17), в гексагональной или шестигранной призме — семь плоскостей симметрии — три плоскости пройдут через противоположные ребра (рис. 18, плоскости а), три плоскости через середины противоположных граней (параллельных продольной оси многогранника — на рис. 18, плоскости Ь) и одна плоскость - перпендикулярно ей (рис. 18, плоскость Л).

Плоскость симметрии обозначается заглавной буквой латинского алфавита Р, а коэффициент, стоящий перед ней, показывает количество плоскостей симметрии в многограннике. Таким образом, для куба можно записать 9Р, т. е. девять плоскостей симметрии, а для гексагональной призмы — 7 Р.
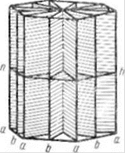
Рис. 18. Плоскости симметрии в гексагональной призме (слева) и схема расположения осей симметрии (в плане, справа)
Ось симметрии. В кристаллических многогранниках можно найти оси, при .вращении вокруг которых кристалл будет совмещаться со споим первоначальным положением при повороте на определенный угол. Такие оси называются осями симметрии.
Ось симметрии кристаллического многогранника -это линия, при вращении вокруг которой правильно повторяются одинаковые элементы ограничения и другие свойства кристалла.
Оси симметрии обозначаются заглавной латинской буквой /-. При вращении кристалла вокруг оси симметрии элементы ограничения и другие свойства кристалла будут повторяться определенное количество раз. Если при повороте кристалла па 360° многогранник совмещается со своим исходным положением дважды, имеют дело с осью симметрии второго порядка, при четырех- и шестикратном совмещениях - соответственно с осями четвертого и шестого порядков. Оси симметрии обозначаются: Ј2— ось симметрии второго порядка; и— ось симметрии третьего порядка; /И — ось симметрии четвертогопорядка; Iй -ось симметрии шестого порядка.
Я7
:м.
Порядком оси симметрии называется количество совмещений кристалла с первоначальным положением при повороте на 360°.
Рис. 19. Оси симметрии в кубе
В связи с однородностью кристаллического строение и благодаря закономерностям в распределении части' внутри кристаллов, в кристаллографии доказываете . возможность существования только вышеперечисленных
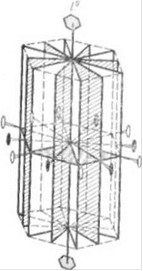
Рис 20. Оси симметрии шестого и второго порядков (L4iU) п плоскости симметрии (7Р) в гексагональной призме
осей симметрии. Ось симметрии первого порядка в расчет не принимается, так как она совпадает с любым направлением каждой фигуры. В кристаллическом многограннике может быть несколько осей симметрии различных порядков. Коэффициент, стоящий перед символом оси симметрии, показывает количество осей симметрии того нлп иного порядка. Так, и кубе три оси симметрии четвертого порядка 3// (через середины противоположных граней); четыре оси третьего порядка —4Ь3 (проводятся через противоположные вершины трехгранных углов) и шесть осей второго порядка б/-2 (через середины противоположных ребер) (рис. 19).
В гексагональной призме можно провести одну ось шестого порядка и б осей второго ' порядка (рис. 18 и 20). 28
В кристаллах наряду с обычными осями симметрии, охарактеризованными ранее, выделяют так называемые инверсионные оси.
Инверсионной осью кристалла называется линия, при вращении вокруг которой на некоторый определенный угол и последующим отражением в центральной точке многогранника (как в центре симметрии) совмещаются одинаковые элементы ограничения .
Инверсионная ось обозначается символом Z.,-. На моделях кристаллов, где обычно приходится определять инверсионные оси, центр симметрии отсутствует. Доказана возможность существования инверсионных осей следующих порядков: первого Ltt, второго Ltt, третьего Li , четвертого 1.^, шестою L,e . Практически приходится иметь дело лишь с инверсионными осями четвертого и шестого порядков (рис. 21).
Иногда инверсионные оси обозначаются цифрой, стоящей справа внизу от символа осн. Так, инверсионная ось второго порядка обозначается символом Li, третьего — L3, четвертого L,„ шестого Le.
Инверсионная ось представляет собой как бы совокупность простой оси симметрии и центра инверсии (симметрии). На приводимой схеме (рис. 21) показаны две инверсионные осп Li ь и Lj4. Разберем оба случая нахождения данных осей в моделях. В трпгональной призме (рис. 21,/) прямая LL — ось третьего порядка /А В то же время она одновременно является инверсионной ОСЬЮшестого порядка. Так, при повороте на 60° вокруг оси любых частей многогранника и последующего отражения их в центральной точке фигура совмещается сама с собой. Иными словами, поворот ребра АВ этой призмы па 60" вокруг LL приводит его в положение А\В\, отражение ребра A\Bi через центр совмещает его с DF.
В тетрагональном тетраэдре (рис. 21,//) все грани состоят из четырех совершенно одинаковых равнобедренных треугольников. Ось LL—ось второго порядка /А При повороте вокруг нее па 180° многогранник сопме-
Т
Рис. 21. Инверсионные оси шестого (/) п четвертого (//) порядков
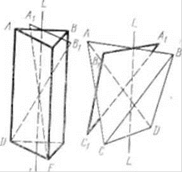
іцается с первоначальным положением, а грань ABC переходит на место ABD. В то же время ось I.2 является и инверсионной осью четвертого порядка. Бели повернуть грань ABC на 90° вокруг оси LL, то она займет положение A\B\d. При отражении ЛібіСі в центральной точке фигуры грань совместится с положением BCD (точка Л| совпадает с С, Вх — с D и С, — с В). Проделав такую же операцию со всеми частями тетраэдра, заметим, что он совмещается сам с собой. При повороте тетраэдра на 360е' получим четыре таких совмещения. Сл едова тел ь-но, LL — инверсионная ось четвертою порядка Li,.
Центр симметрии.
В кристаллических многогранниках, кроме плоскостей и осей симметрии, может быть также и центр симметрии (инверсии).
Центром симметрии (инверсии) кристаллического многогранника называется точка, лежащая внутри кристалла, вдиаметрально противоположных направлениях пт которой располагаются одинаковые элементы ограничения и другие свойства многогранника.
Центр симметрии обозначается буквой С латинского алфавита. При наличии центра симметрии в кристалле каждой грани отвечает другая грань, рапная и параллельная (обратно параллельная) первой. В кристаллах не может быть более одного центра симметрии. В кристаллах любая линия, проходящая через центр симметрии, делится пополам.
Центр симметрии легко найти в кубе, октаэдре, ївгексагональной призме, так как он находится в этих многогранниках в точке пересечения осей и плоскостей симметрии.
Разобранные элементы, встречаемые в кристаллических многогранниках,— плоскости, оси, центр симметрии — называются элементами симметрии.
Виды симметрии
В кристаллах элементы симметрии находятся во взаимосвязи. Благодаря зависимости одних элементов симметрии от других, взаимные сочетания нх весьма ограничены. Установлено, что возможны только 32 комбинации различных группировок, или 32 кристаллографических класса, пли вида симметрии (табл. 1). Данные 32 вида симметрии сначала были выведены чисто теоретически в 1831 i. II. Гессслем, а затем независимо от него русским акад. Л. В. Гадолииым в 1867 г. Позднее этот вывод был подтвержден и на кристаллах.
В каждый вид симметрии объединяются кристаллы на основании совокупности элементов симметрии или наличия какого-либо одного определенного элемента и отсутствия других элементов симметрии.
Иными словами, вид симметрии кристалла — это полная совокупность его элементов симметрии.
Виды симметрии, в которых имеются только главные оси, названы примитивными. Если в видах симметрии присутствует и центр симметрии, они называются центральными. При наличии плоскости говорят о планальном виде симметрии (грсч. «планум» — плоскость), если имеются только оси — аксиальный вид симметрии (греч. «аксон» ось). Максимальное количество возможных осей и плоскостей дает наименование планиксиального вида симметрии. В случае присутствия инверсионных осей говорят об инверсионно-примитивном или инверсионно-пла-нальном видах симметрии.
При определении кристаллов или нх моделей следует иметь в виду, что найденная комбинация элементов симметрии должна непременно соответствовать определенному виду симметрии из приводимых 32 классов (табл. 1).
Сингонии
Кристаллографические классы, или виды симметрии, объединяются в более крупные группировки, называемые системами или сингониями. Таких сингонии семь:
1) кубическая — высшая категория
2) гексагональная Ў
3) тетрагональная средняя категория
4) тригональная ;
5) ромбическая I
6) моноклинная ; низшая категория.
7) триклинная '
В каждую сингонию входят кристаллы, у которых отмечается одинаковое расположение кристаллографических осей и одинаковые элементы симметрии. Сингонией называется группа видов симметрии, обладающих одним или несколькими одинаковыми элементами симметрии и имеющих одинаковое расположение кристаллографических осей.
Охарактеризуем каждую сингонию.
Высшая категория. Кубическая сингония. В этой сингонии кристаллизуются наиболее симметричные кристаллы. В кубической сингонии присутствует более одной осп симметрии выше второго порядка, т. е. Ь,3 или I4. Кристаллы кубической сингонии обязательно должны иметь четыре оси третьего порядка (4Ј3) и, кроме того, либо три взаимно перпендикулярные оси четвертого порядка (3/.*), либо три оси второго порядка (З/.2). Максимальное количество элементов симметрии в кубической сингонии может быть выражено формулой ЗШЈ36/.29РС.
Кристаллы кубической сингонии встречаются в виде куба, октаэдра, тетраэдра, ромбододекаэдра, пентагон-додекаэдра и др. (рис. 22). В кубической сингонии кристаллизуются следующие минералы: каменная соль (га-лит), пирит, галенит, флюорит и др.
Сингонии средней категории. Эта группа объединяет кристаллы, обладающие только одной осью симметрии порядка выше второго. К средней категории относятся гексагональная, тетрагональная и тригопальная сингонии.
Гексагональная сингония характеризуется наличием одной оси симметрии шестого порядка (/-6). Максимальное количество элементов симметрии может быть следующим: 1*в6Ь27РС. Кристаллы гексагональной сингонии образуют призмы, пирамиды, днпирамнды и др. (рис. 23).В гексагональной сингонии кристаллизуются апатит, нефелин, берилл и другие минералы.
Тетрагональная сингония имеет одну ось четвертого порядка (/.4). Максимальная симметрия для этой сингонии характеризуется формулой /,44125РС. Формы кристаллов данной сингонии - тетрагональные призмы, пирамиды, дипирамиды и их комбинации (рис. 24). К тет-
Рис. 22. Кристаллы кубической сннгоннн:
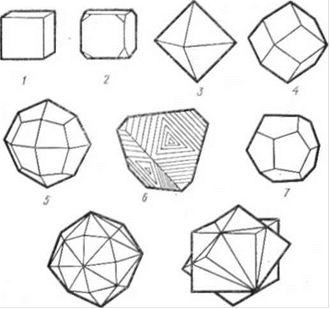
Рис. 24. Кристаллы тетрагональной сиигонии:
Дата добавления: 2015-06-27; просмотров: 1285;
