Зависимость температуры плавления металлических нанокластеров от их размера.

Равновесие данного фазового состояния (газообразного, жидкого, твердого) системы частиц, например, атомов, оценивается исходя из стремления к минимуму свободной энергии, в частности, свободной энергии Гиббса G.

Температуру плавления отдельных кристаллических нанокластеров определяют как температуру, при которой частицы одинакового состава и массы, находящиеся как в жидком, так и в твердом состоянии имеют одинаковую величину G.

В случае перехода нанокластера сферической формы радиуса R из твердого в жидкое состояние происходит изменение свободной энергии DG_∑

DG_∑ = DG_v4pR³r_т/3 + Dg4pR²,

где DG_v –изменение молярной свободной энергии при плавлении, r_т молярная плотность твердого материала, Dg – разница удельных поверхностных энергий жидкого и твердого состояний.

Изменение энергии DG_v4pR³r_т/3 возникает за счет плавления нанокластера данного объема, а Dg4pR² соответствует разнице поверхностной энергии жидкого и твердого нанокластеров.

Плавление нанокластеров ниже температуры плавления Т_пл тела макроразмеров сопровождается увеличением G_v (+DG_v)и уменьшением g (- Dg).

Отсюда

DG_∑ = DGv4pR³r_т/3 - Dg4pR²

В этом случае графическая зависимость DG_v, Dg_s и DG_∑ от R имеет вид (рис. 2.5)

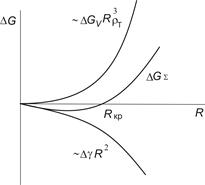
Рис. 1. Изменение свободной энергии наночастицы, находящейся в жидком состоянии, при увеличении ее размера

Из анализа соотношения для DG_∑ и кривой DG_∑ от R следует, что равенство свободных энергий (DG_∑ = 0) наступает при некотором размере кластера R_кр

R_кр = 3Dg/r_тDG_v

Если R меньше R_кр, то нанокластер находится в жидком состоянии, если больше R_кр то в твердом.Температура плавления2.swf

При переходе кластера из твердого в жидкое состояние происходит поглощение энергии, соответствующее

DG_v = Q_плDТ /Т_пл,

где DТ – разница температур плавления массивного материала и нанокластера радиуса R_кр.

В результате

R_кр =3Dg/(r_тQ_плDТ/ Т_пл)

Отсюда следует, что температура плавления нанокластера Т(R) = Т_пл - DТ зависит от его размера (рис. 2)

Т(R) = Т_пл (1 – 3Dg/(r_тQ_плR_кр))

Рис. 2. Зависимость температуры плавления нанокластера Т(R) от его размера.

Проявление на практике:

Снижение температуры спекания нанопорошков (топливных нанотаблеток).

Необходимость сильного переохлаждения для получения нанообъектов.

Нестабильность нанообъектов при нагреве.

Теплоемкость нанокластеров

Как известно, молярная теплоемкость C макроскопических металлических тел описывается законом Дюлонга и Пти,

C = 3R,

где R – газовая постоянная.

Данный закон учитывает только составляющую теплоемкости, обусловленную тепловыми колебаниями атомов в объеме макроскопических тел при температурах больше температуры Дебая (температура, выше которой можно не принимать во внимание квантовые эффекты связанных колебаний атомов).

Температура Дебая — температура, при которой возбуждаются все моды колебаний в данном твёрдом теле. Мода - тип колебаний, характеризующийся своей собственной частотой. Дальнейшее увеличение температуры не приводит к появлению новых мод колебаний, а лишь ведёт к увеличению амплитуд уже существующих, т. е. средняя энергия колебаний с ростом температуры растёт. Температура Дебая приближённо указывает температурную границу, ниже которой начинают сказываться квантовые эффекты.

При этом не рассматриваются вклады в теплоемкость, связанные с поглощением энергии за счет:

- колебаний поверхностных атомов, так как для макротел мала доля поверхностных атомов по отношению к атомам внутри объема,

- появления вакансий, которые также составляют малую долю от числа атомов объема вплоть до температуры плавления,

- возбуждения электронов электронного газа, который дает основной вклад в теплоемкость только при очень низких температурах,

-теплового расширения, вклад которого составляет незначительную величину (доли процента),

- возбуждения электронов, находящихся на частично заполненных уровнях переходных металлов.

Квантовый характер связанных колебаний атомов проявляется в том, что ниже температуры Дебая существенно уменьшается число колебательных мод.

Это объясняется тем, что при температурах выше дебаевских колебательный спектр представлен как низкочастотными, так и высокочастотными модами колебаний (рис. 1), которые рассматриваются как стоячие волны, соответствующие энергии

E = hn

или

E = hc/l,

где h - постоянная Планка, n - частота, c – скорость звука в среде, l - длина волны.

Самая большая длина волны соответствует l_max = 2L, при частоте w _min = 2pc/l _max = pc/L

где L – размер тела, самая малая длина волны равна

l_min = 2a, при частоте w _max = 2pc/l _min= pc/a

где a – межатомное расстояние.

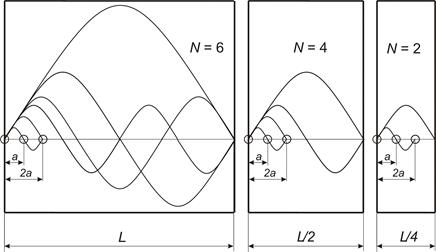
Рис. 1. Изменение количества колебательных мод стоячих волн при уменьшении размера наночастицы (амплитуда колебаний на рисунке не имеет количественной оценки). При размере L присутствует 6 мод, при L/2 – 4 моды, при L/4 – 2 моды. За счет уменьшения размеров спектр колебаний (набор длин волн и частот) обедняется за счет длинноволновых мод.

При переходе к наноразмерам происходит изменение теплоемкости по сравнению с макроразмерами. При этом возможен как рост, так и снижение теплоемкости:

- рост теплоемкости, вызванный увеличением вклада низкочастотных мод колебаний, обусловленных аморфной структурой поверхностных слоев нанокластера;

- снижение теплоемкости, происходящее за счет обеднения колебательного спектра длинноволновыми модами вследствие уменьшения максимальной длины волны l_max;

- снижение теплоемкости из-за увеличения разницы между уровнями энергий, на которых могут находиться электроны.

Для отдельных нанокластеров и компактированной структуры из нанокластеров определяющим фактором является аморфная структура поверхностных слоев нанокластеров, отличающаяся высокой концентрацией дефектов, в частности вакансий. Данный вклад, увеличивающий теплоемкость, оказывается больше, чем снижение теплоемкости вследствие уменьшения максимальной длины волны, вызванное уменьшением размеров. Это подтверждается экспериментальными зависимостями теплоемкости от температуры для компактированной структуры из нанокластеров меди (8нм) и палладия (6нм) (рис. 2).

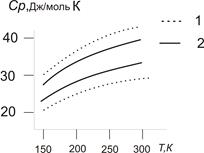
Рис. 2. Температурная зависимость теплоемкости палладия (1) и меди (2) для наноструктурированного (верхняя) и обычного (нижняя) массивного материала.

В низкотемпературной области проявление квантовых эффектов вызывает уменьшение плотности колебательных состояний за счет малой вероятности возбуждения высокочастотных мод колебаний. Это приводит к уменьшению теплоемкости как для наноразмерных, так и для макроразмерных структур (рис. 3).

При температурах ниже 1К (рис. 3.) теплоемкость отдельных нанокластеров становится меньше теплоемкости макроразмерных тел, что можно объяснить тем, что разница между энергетическими уровнями электронов DW в нанокластерах становится существенно больше kT, в то время как в случае макроразмеров DW остается меньше kT.

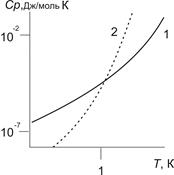
Рис. 3. Зависимость от температуры теплоемкости нанокластера серебра (10нм) при низких температурах. 1 – для макроразмерного образца, 2 – для нанокластера.