Кинетика обратимой реакции первого порядка
В биологических системах большая часть реакций является обратимыми, то есть одновременно протекают в обоих направлениях: А«В. Кинетика такой реакции рассматривается как две одновременно протекающие реакции – прямую и обратную с константами скоростей k1 и k-1.
Кинетическое уравнение выглядит следующим образом:
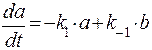 .
.
Кроме начальных условий t=0, a=a0, b=0, мы можем наложить ограничение замкнутости системы, следовательно: a+b=aо в любой момент времени.
Тогда кинетическое уравнение будет выглядеть следующим образом:
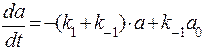 .
.
Дифференциальные уравнения такого типа решаются в два этапа. Сначала находим решение однородного уравнения:
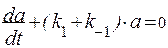
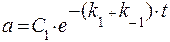
Частное решение неоднородного уравнения с постоянной правой частью находим в виде константы а = С и тогда
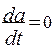 ,
, 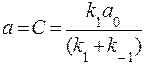 .
.
Константу интегрирования можно определить из начальных условий t=0, a=a0, тогда общее решение дифференциального уравнения запишется следующим образом:
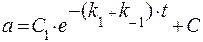
В результате вычислений подставляя значения С:
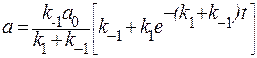
Учитывая, что b=a0-a, получим:
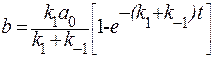
Кинетика реакции второго порядка
Реакция 2-го порядка имеет вид: 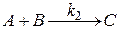 ,
,
и с учетом того, что при t = 0, исходные концентрации равны a0 и b0, в любой момент времени на основании эквимолярного взаимодействия a и b:
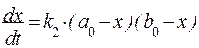
Проведя разделение, переменных получим:
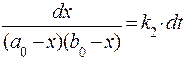
Используя тождество:
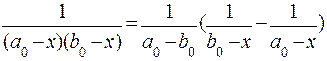 ,
,
получим стандартное дифференциальное уравнение:
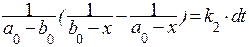 .
.
Его решение:
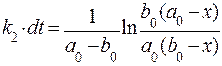 .
.
При избытке одного из веществ это выражение превращается в уравнение 1-го порядка.
Дата добавления: 2015-06-22; просмотров: 1318;
