Перенос молекул через мембраны. Уравнение Фика
Важным элементом функционирования мембран является их способность пропускать или не пропускать молекулы (атомы) и ионы. Существенно, что вероятность такого проникновения частиц зависит как от направления их перемещения, например, в клетку и из клетки, так и от разновидности молекул и ионов.
Эти вопросы рассматриваются в разделе физики, относящимся к явлениям переноса. Таким термином называют необратимые процессы, в результате которых в физической системе происходит пространственное перемещение (перенос) какой-либо физической величины.
К явлениям переноса относятся следующие физические явления: диффузия, теплопроводность, внутреннее трение. Эти явления объединяются тем, что переносится какая-либо физическая характеристика: масса молекул (при диффузии), энергия (при теплопроводности), количество движения (при внутреннем трении).
Такой подход позволяет получить для них одно общее уравнение.
Действительно, пусть через ∆S за время ∆t в одном направлении проходит N молекул
 |
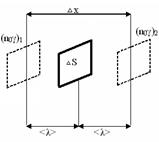Рисунок 12.
Обозначим физическую характеристику переносимую каждой молекулой через γ (рис.12).
Тогда
.
Это перенос слева направо. Справа налево аналогично. Если по обе стороны ∆S разная степень неоднородности характеристики, то будет иметь место преимущественный перенос.
.
Умножим и разделим правую часть на 2<λ>
.
Величина 
.
Поэтому 
.
Это и есть уравнение переноса в общем виде.
Применим его к описанию процессов диффузии и теплопроводности. При диффузии переносится масса, то есть 
.
,
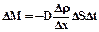где 
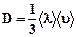- коэффициент диффузии.
Масса газа, переносимая вследствие диффузии через площадь ∆S перпендикулярную направлению, в котором убывает плотность, пропорциональна ее площади, промежутку времени переноса и градиенту плотности (закон Фика).
Он применим не только для газов, но и для жидкостей и твердых тел, но у них коэффициент диффузии значительно меньше.
Частным случаем диффузии является осмос – явление диффузии растворителя через полупроницаемую перегородку, отделяющую раствор от чистого растворителя.
Давление, возникающее при такой (односторонней) диффузии называется осмотическим и пропорционально концентрации и температуре раствора, а обратнопропорционально молярной массе растворенного вещества.
Такая зависимость выражается законом Вант-Гоффа
,
где с = m/V - концентрация раствора, m – масса растворенного вещества, V - объем раствора.
При теплопроводности переносимой величиной является энергия, а, следовательно, и количество теплоты.
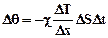- уравнение Фурье
где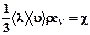 
– коэффициент теплопроводности
Количество теплоты, переносимое сквозь площадку ∆S перпендикулярную направлению, в котором убывает температура, пропорционально площади ∆S, промежутку времени ∆t переноса и градиенту температуры ∆Т/∆х (уравнение теплопроводности).
Уравнение применимо также для жидкостей и твердых тел.
При внутреннем трении переносится импульс.
,
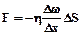где 
- коэффициент внутреннего трения (вязкость).
Сила внутреннего трения, возникающая в плоскости соприкосновения двух скользящих относительно друг друга слоев, пропорциональна площади из соприкосновения ∆S и градиенту скорости ∆ω/∆х (закон Ньютона).
Вопросы для самоконтроля
1) Что называется термодинамической системой?
2) Какой термодинамические процесс называется обратимым?
3) Сформулируйте первое и второе начала термодинамики.
4) Что называется энтропией?
5) Свойства энтропии.
6) Поясните принцип минимума производства энтропии.
7) В каких случаях изменение внешних условий может привести к гибели организма?
8) Опишите строение мембран.
9) Как называется явление переноса массы вещества, и каким уравнение оно описывается?
СПИСОК ЛИТЕРАТУРЫ
Основная
1. Пронин, В.П. – Краткий курс физики/ В.П. Пронин. – Саратов. СГАУ. 2007 г., 200с.
2. Рогачев, Н.М. – Курс физики. Учебное пособие/ Н.М. Рогачев. – С.-Петербург: Издательство «Лань», 2010г.- 448с.
3. Телесин, Р.В. – Молекулярная физика: Учебное пособие 3-е издание/ Р.В. Телесин. –
С.-Петербург: Издательство «Лань», 2009г.- 368с.
4. Основы физики и биофизики./ А.И. Журавлев [и др.] М.: Мир. 2005. – 384 с.
5. Термодинамика. Учебное пособие / И.П. Чернов, [и др.] – М.: «Высш. школа». - 2007. – 405 с.
Дополнительная
1. Белановский, А.С. Основы биофизики в ветеринарию/А.С. Белановский. – М.: Агропром–ИЗДАТ, 1989-271с.
2. Грабовский, Р.И. – Курс физики. 6-е изд./ Р.И. Грабовский – С.-Петербург: Издательство «Лань», 2002.- 608 с.
3. Медицинская и биологическая физика: Учеб. Для вузов/ А.Н. Ремизов [и др.] – 4-е изд., перераб. и дополн.. – М.: Дрофа, 2003. – 560 с.
Дата добавления: 2015-06-22; просмотров: 905;