ИЗМЕРЕНИЕ АКТИВНОГО, ЕМКОСТНОГО И ИНДУКТИВНОГО СОПРОТИВЛЕНИЙ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Рассмотрим цепь, содержащую только резистор R с омическим сопротивлением R (рис. 1).
Сопротивление R резистора называют активным, так как в нем происходит необратимая потеря электрической энергии, переходящей в тепловую.

Рис.1
К зажимам цепи приложено переменное напряжение
UR = Umax * Cos 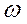 t (1)
t (1)
где umax – амплитудное значение напряжения, 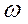 - круговая частота.
- круговая частота.
Величину тока, проходящего через резистор, определим исходя из закона Ома:
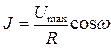 t = J max cos wt (2)
t = J max cos wt (2)
где 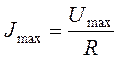 - амплитудное значение силы тока. Из формул (1) и (2) видно, что сила тока и напряжение на активном сопротивлении изменяются в одной фазе – гармонически (рис.2), их можно представить с помощью векторной диаграммы (рис.3).
- амплитудное значение силы тока. Из формул (1) и (2) видно, что сила тока и напряжение на активном сопротивлении изменяются в одной фазе – гармонически (рис.2), их можно представить с помощью векторной диаграммы (рис.3).
Вектор, изображающий амплитудное значение силы тока Jmax , обычно откладывается вдоль горизонтальной оси, взятой за начало отсчета.
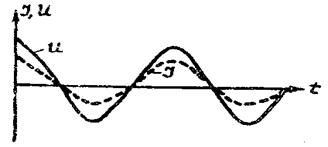
Рис.2
Угол между амплитудным значением тока и напряжением называют фазовым. В цепи, содержащей только активное сопротивление, сдвиг фаз между силой тока и напряжением отсутствует, а поэтому вектор напряжения будет направлен так же, как и вектор тока, т.е. вдоль оси токов (рис.3).

Рассмотрим цепь, содержащую катушку индуктивности с индуктивностью L (рис.4), омическое сопротивление которой будем считать равным нулю.

Рис.4
Напряжение на зажимах цепи будет:
UL = Umax * cos 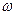 t (3)
t (3)
По закону Ома для участка цепи при R = 0 будем иметь
UL = 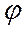 1 -
1 - 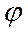 2 =
2 = 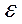 L (4)
L (4)
(будем считать, что приложенное напряжение уравновешивается электродвижущей силой самоиндукции, равно ей по значению и противоположно по направлению),
где 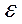 L - ЭДС самоиндукции, которая по основному закону электромагнитной индукции будет равна:
L - ЭДС самоиндукции, которая по основному закону электромагнитной индукции будет равна:
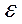 L = - L
L = - L 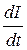 (5)
(5)
Учитывая формулы (3) , (4) и (5), получим :
Umax Cos 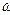 t = L
t = L 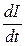 (6)
(6)
Выделив переменные в (6) и проинтегрируя его, найдем :
I = 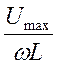 Sin
Sin 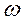 t = Jmax cos (
t = Jmax cos ( 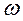 t -
t - 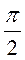 ) , (7)
) , (7)
где Imax = 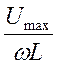 - амплитудное значение тока. RL =
- амплитудное значение тока. RL = 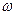 L – называется индуктивным сопротивлением. На индуктивном сопротивлении не происходит потери энергии и его называют реактивным сопротивлением.
L – называется индуктивным сопротивлением. На индуктивном сопротивлении не происходит потери энергии и его называют реактивным сопротивлением.
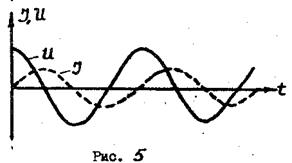
Из (7) и (3) следует, что сила тока отстает от напряжения (рис. 5). Причиной этого является ЭДС самоиндукции. На рис. 6 представлена векторная диаграмма напряжения и тока в цепи с индуктивностью.

Рассмотрим цепь, содержащую конденсатор емкостью С (рис. 7).

Напряжение на зажимах цепи:
Uc = Umax cos 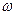 t (8)
t (8)
А сила тока
I = 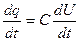 , (9)
, (9)
На основании (8) получим:
I = - Umax 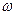 c Sin
c Sin 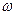 t = Jmax Cos (
t = Jmax Cos ( 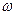 t +
t + 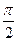 ), (10)
), (10)
где Jmax = Umax c 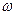 (11)
(11)
Jmax - амплитудное значение силы тока.
Величина 
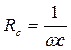

называется емкостным сопротивлением и так же как индуктивное называется реактивным сопротивлением. Оно зависит от емкости конденсатора и частоты.
Из /8/ и /10/ следует, что в цепи с емкостным сопротивлением напряжение на конденсаторе отстает по фазе от колебаний силы тока на величину π/2.
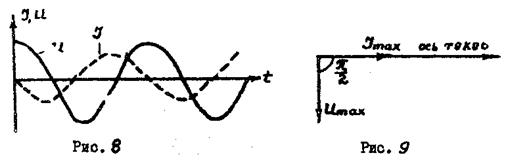
Векторная диаграмма полученных результатов представлена на рис.9.
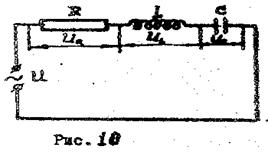
Рассмотрим цепь, содержащую резистор, катушку и конденсатор /рис.10/.
Как было изложено выше, сила тока в цепи и напряжение изменяются не в одной фазе, т. е. если сила тока изменяется по закону:
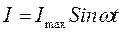
то напряжение по закону :
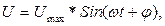
где φ-сдвиг фаз между током и напряжением. Полное сопротивление цепи называется импедансом и обозначается Ż.
Для нахождения импеданса и сдвига фаз, воспользуемся векторной диаграммой / рис.11/.Амплитуды напряжений на всех участках будем
откладывать относительно силы тока, т.к. она во всей цепи одинакова. На резисторе векторы напряжения и силы тока совпадают, т.к. они не имеют разности фаз.
На индуктивном сопротивлении вектор напряжения опережает силу тока по фазе на π/2, а на емкостном- отстает на π/2. Результирующий вектор найдем путем сложения трех векторов. Векторы UmaxL и UmaxC направлены по одной прямой в противоположные стороны. Полученные векторы (UmaxL- UmaxC) и UmaxR складываются по правилу параллелограмма и находится результирующий вектор Umax0,т.е.:
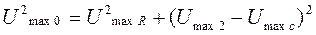 /13/
/13/
Учитывая, что
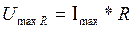 ; UmaxL=Imax*ωL; Umaxc=Imax*
; UmaxL=Imax*ωL; Umaxc=Imax* 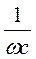 . (14)
. (14)
получим:
I2max R20 = J2max R2 + J2max (RL – Rc )2 (15)
Обозначим R0 через Z – полное сопротивление цепи или импеданс, тогда
Z = 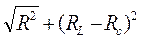 (16)
(16)

Из рис. 11 получаем
tg 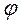 =
= 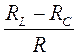 (17)
(17)
Закон Ома для рассматриваемой цепи будет иметь вид:
Jmax = 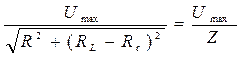 (18)
(18)
Электроизмерительные приборы показывают не амплитудные значения тока и напряжения, а эффективные, которые связаны между собой следующим образом:
Iэф = 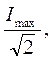 Uэф=
Uэф= 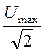 ,
,
Тогда выражение /18/ примет вид:
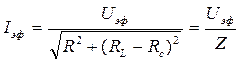 /19/
/19/
II. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ.
Переносной измерительный комплект типа К-50 имеет постоянно смонтированную схему и предназначен для постоянных измерений силы тока, напряжения и мощности в однофазных и трехфазных цепях переменного тока.
На общей панели смонтированы все элементы схемы измерительного комплекта К-50. Все необходимые соединения между элементами схемы выполнены постоянным монтажом.
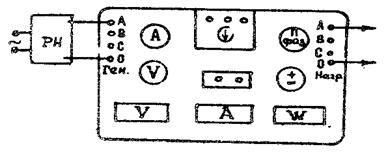
Рис.12
Кроме крышек измерительных приборов над лицевой стороной панели выступают: ручки переключателей, зажимы, крышка фазоуказателя и кнопка, карболитавая панель со штырьковым переключателем и потенциальными зажимами. Корпус комплекта имеет съемную крышку, на внутренней стороне которой укреплена табличка- инструкция К-50.
Схема включения измерительного комплекта приведена на рис. 12.
Комплект включения в сеть через ЛАТP РН.
III. ПОРЯДОК ВЫПОЛНЕНЯ РАБОТЫ.
ВНИМАНИЕ: подключение комплекта К-50 можно производить только при отключенном источнике питания.
1. Установите комплект в горизонтальное положение.
2. Подключите источник питания к группе зажимов, обозначенных “ген”, нагрузку подключите ко второй группе зажимов, имеющих обозначение ”нагр”. /рис.13/.
3. Установите переключатель фаз комплекта в положение “0”, переключатель номинальных напряжений в положение 600 В, переключатель номинальных токов в положение 50 А, переключатель полярности ваттметра в положение”+”, колодку “К” (штыковый переключатель с обозначением стрелки) установите стрелкой в сторону приборов (рис. 13).
4. Установите стрелки приборов с помощью корректоров на нулевые отметки шкал.
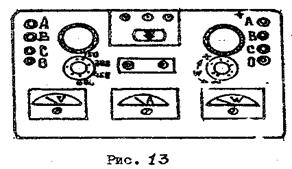
5. Поставьте переключатель фаз в положение фазы, в которой хотят произвести измерения.
Если отклонение стрелки амперметра будет меньше 50 % верхнего предела измерения (отметка 50), то переключатель номинальных токов перевести на меньший предел измерения.
Если отклонение стрелки вольтметра будет меньше 50 % от верхнего предела измерения (отметка 75), то переключатель напряжений перевести на меньший предел измерений.
ЗАДАНИЕ 1. ОПРЕДЕЛЕНИЕ АКТИВНОГО СОПРОТИВЛЕНИЯ
1. Подключите к клеммам «нагр» ламповый реостат – позиция 1. (рис. 14), определяя при этом Iэф и Uэф  по амперметру и вольтметру.
по амперметру и вольтметру.
2. Определите активное сопротивление по формуле:
R = 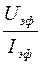
ЗАДАНИЕ 2. ОПРЕДЕЛЕНИЕ ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ И ИНДУКТИВНОСТИ КАТУШКИ.
1. Подключите к клеммам «нагр» ламповый реостат и катушку индуктивности (поз. II. Рис. 14).
2. Изменяя подаваемое в схему напряжение U с помощью ЛАТР – а РН, запишите соответствующее ему значение силы тока Iэф.
3. Рассчитайте полное сопротивление Z = 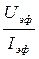 при различных напряжениях и найдите Z ср.
при различных напряжениях и найдите Z ср.
4. Рассчитайте индуктивное сопротивление RL = 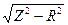 и индуктивность катушки
и индуктивность катушки
L = 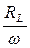
где 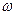 = 2
= 2 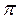 f, f = 50 Гц, (активное сопротивление катушки указано на его корпусе); R – активное сопротивление катушки и лампового реостата.
f, f = 50 Гц, (активное сопротивление катушки указано на его корпусе); R – активное сопротивление катушки и лампового реостата.
5. Результаты измерений и вычислений занесите в табл. 1.
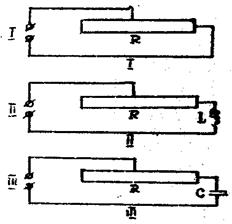
Рис. 14.
Таблица 1
Результаты измерений и вычислений RL и L
| №№ п.п. | Uэф, В | Jэф, А | Z, Ом | Zср, Ом | RL, Ом | L Гн |
ЗАДАНИЕ 3. ОПРЕДЕЛЕНИЕ ЕМКОСТНОГО СОПРОТИВЛЕНИЯ И МКОСТИ КОНДЕНСАТОРА
1. Подключите к клеммам «нагр» ламповый реостат, и конденсатор (поз.III рис. 14).
2. Последовательно подавая в цепь различные напряжения Uэф , (изменяя его ЛАТРом РН), измерьте соответствующие силы токов Iэф.
3. Рассчитайте полное сопротивление Z при различных напряжениях и найдите его среднее значение Zср .
4. Рассчитайте емкостное сопротивление и емкость конденсатора:
Rc = 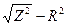 ; C =
; C = 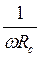
5. Результаты измерений и вычислений занесите в таблицу 2.
Таблица 2.
Результаты измерений и вычислений Rc и С
| №№ п.п. | Uэф, В | Jэф, А | Z, Ом | Zср, Ом | Rс, Ом | С, ф |
Дата добавления: 2015-06-17; просмотров: 3347;
