Истечение жидкости через малое отверстие при постоянном напоре

 Отверстие называется малым, когда его вертикальный размер меньше 0,1 расчетного напора Нр (понятие об Нр приведено ниже): для круглого отверстия dо<0,1Нр (рис. 6.1) При таком условии можно считать, что давление и скорость жидкости во всех точках сечения малого отверстия одинаковы. Отверстие может быть выполнено в виде сверления в тонкой стенке (δ<0,67 Нр) без обработки входной кромки или в толстой стенке, но с заостренными краями кромки с внешней стороны (рис. 6.2). Условия истечения жидкости в этих случаях будут одинаковы. Частицы жидкости приближаются к отверстию из всего объема, двигаясь ускоренно по плавным траекториям. Например, частицы жидкости, двигающиеся у вертикальной стенки к отверстию, должны повернуть на угол 900 при выходе наружу. Поскольку частицы жидкости обладают массой и, соответственно, свойством инерционности, то они огибают входную кромку по некоторой кривой. Поэтому, на расстоянии l=(0,5…1,0)do образуется так называемое сжатие струи, т.е. площадь сечения струи Sс меньше площади отверстия So. Степень сжатия струи оценивается коэффициентом сжатия струи εо:
Отверстие называется малым, когда его вертикальный размер меньше 0,1 расчетного напора Нр (понятие об Нр приведено ниже): для круглого отверстия dо<0,1Нр (рис. 6.1) При таком условии можно считать, что давление и скорость жидкости во всех точках сечения малого отверстия одинаковы. Отверстие может быть выполнено в виде сверления в тонкой стенке (δ<0,67 Нр) без обработки входной кромки или в толстой стенке, но с заостренными краями кромки с внешней стороны (рис. 6.2). Условия истечения жидкости в этих случаях будут одинаковы. Частицы жидкости приближаются к отверстию из всего объема, двигаясь ускоренно по плавным траекториям. Например, частицы жидкости, двигающиеся у вертикальной стенки к отверстию, должны повернуть на угол 900 при выходе наружу. Поскольку частицы жидкости обладают массой и, соответственно, свойством инерционности, то они огибают входную кромку по некоторой кривой. Поэтому, на расстоянии l=(0,5…1,0)do образуется так называемое сжатие струи, т.е. площадь сечения струи Sс меньше площади отверстия So. Степень сжатия струи оценивается коэффициентом сжатия струи εо:
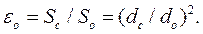 (6.1)
(6.1)
При истечении жидкости необходимо знать скорость и расход. Для этого составим уравнение Бернулли для сечений 1-1 и 2-2, приняв за плоскость сравнения горизонтальную плоскость, проходящую через ось отверстия:
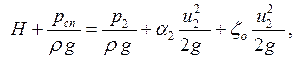 (6.2)
(6.2)
где ζо – коэффициент сопротивления малого отверстия. Обозначим α2=α, u2=u, а р2=рвых (рвых– давление на выходе из малого отверстия). Введем расчетный напор Нр:
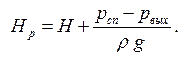
Тогда из уравнения (6.2) получим:
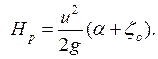 (6.3)
(6.3)
Окончательно, из уравнения (6.3) найдем скорость истечения струи:
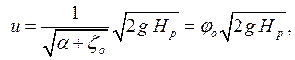 (6.4)
(6.4)
где φо – коэффициент скорости малого отверстия:
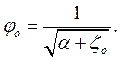 (6.5)
(6.5)
Для гипотетического случая истечения идеальной жидкости ζо=0, а α=1. Тогда φо=1, а скорость истечения идеальной жидкости будет равна:
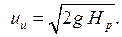 (6.6)
(6.6)
Формула (6.6) совпадает с формулой для расчета свободного падения тела в пустоте и называется формулой Торричелли. Анализ формул (6.4) и (6.6) показывает, что коэффициент скорости φо – это отношение скорости истечения вязкой жидкости к скорости истечения идеальной жидкости:
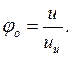 (6.7)
(6.7)
Коэффициент скорости φо всегда меньше единицы, поскольку скорость истечения идеальной жидкости uи больше скорости истечения вязкой жидкости u из-за наличия гидравлического сопротивления: всегда ζо>0.
Поле скоростей в сечении струи является равномерным только в ядре струи, наружный слой жидкости имеет несколько меньшую скорость из-за трения об острую входную кромку малого отверстия. Скорость в ядре струи, как показывают опыты, практически равна идеальной uи. Поэтому коэффициент φо является коэффициентом средней скорости.
Расход жидкости Q при истечении подсчитывают как произведение скорости струи на площадь ее сечения:
 (6.8)
(6.8)
Произведение коэффициентов εо и φо называется коэффициентом расхода µо:
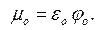 (6.9)
(6.9)
Тогда формулу (6.8) для расчета расхода Q можно записать в следующем виде:
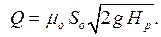 (6.10)
(6.10)
Коэффициенты сжатия струи εо, сопротивления ζо, скорости φо и расхода µо зависят от числа Рейнольдса Re. Поскольку для расчета Re необходимо знать скорость истечения u, а для определения скорости u необходим коэффициент скорости φо, то принято использовать в расчетах число Рейнольдса, подсчитанное для идеальной скорости uи:
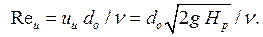 (6.11)
(6.11)
Графические зависимости, составленные А.Д. Альтшулем на основе опытов различных авторов, приведены на рис. 6.3.

Дата добавления: 2015-06-17; просмотров: 911;
