Уравнение Бернулли для элементарной струйки идеальной жидкости и потока вязкой жидкости
В элементарной струйке идеальной жидкости расположим декартовы оси координат таким образом, чтобы ось Z была параллельна вектору ускорения свободного падения g и направлена вертикально вверх. В данном частном случае jx=jy=0 и jz=−g, уравнение (3.10) примет вид:
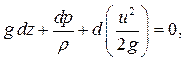 (5.5)
(5.5)
или
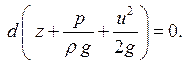 (5.6)
(5.6)
Проинтегрируем уравнение (5.6), в результате получим:
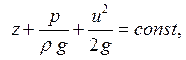 (5.7)
(5.7)
Зависимость (5.7) получена Д. Бернулли в 1738 г. и называется уравнением Бернулли для элементарной струйки идеальной жидкости.
В уравнении (5.7) hпз= р/(ρg) и hг=z, как и в уравнении (3.13) геометрический и пьезометрический напоры, соответственно, hс= u2/(2g) называется скоростным или динамическим напором.
Таким образом, сумма геометрического, пьезометрического и скоростного напоров для любых сечений элементарной струйки идеальной жидкости есть величина постоянная.
Как известно из подраздела 3.3,геометрический напор z – удельная потенциальная энергия жидкости, апьезометрический напор р/(ρg)  – удельная потенциальная энергия давления.
– удельная потенциальная энергия давления.
Известно, что кинетическая энергия Ек выражается формулой: Ек=mu2/2. Кинетическая энергия, отнесенная к единице веса тела mg, называется удельной, т.е. ек= mu2/2g.
Тогда, уравнение (5/7) можно сформулировать следующим образом: сумма удельной потенциальной энергии положения, удельной потенциальной энергии давления и удельной кинетической энергии для любых сечений элементарной струйки идеальной жидкости есть величина постоянная.
Сумма геометрического, пьезометрического и скоростного напоров называется полным напором или полной удельной энергией элементарной струйки (потока) в данном живом сечении, т.е.
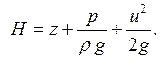 (5.8)
(5.8)
Для вывода уравнения Бернулли для потока вязкой жидкости введем понятие мощности потока. Мощность потока в определенном живом сечении – полная энергия, которую проносит поток через это живое сечение в единицу времени или работа, которую могла бы совершить жидкость, прошедшая через данное живое сечение за единицу времени.
Определим вначале мощность dN элементарной струйки в определенном живом сечении. Поскольку удельная энергия является энергией, отнесенной к единице веса жидкости, то
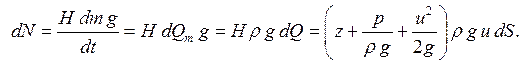 (5.9)
(5.9)
Мощность потока найдем путем интегрирования уравнения (5.9) по площади S:
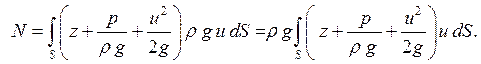 (5.10)
(5.10)
Теоретически и экспериментально доказано, что для параллельноструйчатых или плавно меняющихся потоков гидростатический напор z+p/ρg есть величина, одинаковая для всех точек для всех точек определенного живого сечения потока, т.е. при движении элементарные струйки оказывают одна на другую в поперечном направлении такое же давление, как слои в покоящейся жидкости:
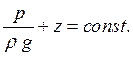
В дальнейшем будем рассматривать такие или близкие к ним живые сечения потока. С учетом этих допущений уравнение (5.10) примет вид:
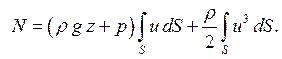 (5.11)
(5.11)
Найдем среднее значение полной удельной энергии (полного напора) в данном живом сечении потока. С учетом зависимости (4.3) получим:
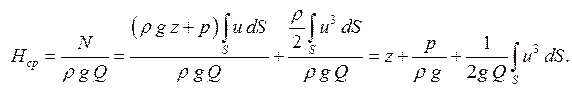 (5.12)
(5.12)
Умножим и разделим последний член уравнения (5.12)на квадрат средней скорости потока u2ср:
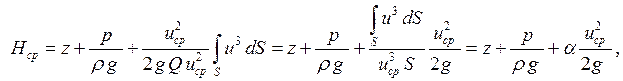
где α – безразмерный коэффициент Кориолиса, учитывающий неравномерность распределения скоростей в живом сечении потока и равный:
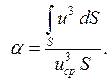 (5.13)
(5.13)
Рассмотрим физическую сущность коэффициента Кориолиса. Для этого разделим и умножим зависимость (5.13) на ρ/2.
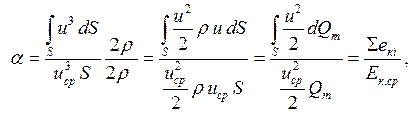
где екi – кинетическая энергия, которой обладает масса i-й элементарной струйки, прошедшая через данное живое сечение в единицу времени; Ек.ср – кинетическая энергия, которой обладает масса потока жидкости, прошедшая через то же живое сечение в единицу времени, и подсчитанная по средней скорости.
Для ламинарного течения жидкости αлам=2, для турбулентного αтурб=1,05…1,15 [1, с.102; 8,с. 140]. При турбулентном течении жидкости, чем выше число Рейнольдса, тем ближе к единице αтурб. Для Re > 104 с достаточной степенью точности для технических расчетов можно считать αтурб=1. Различие в значениях α для ламинарного и турбулентного режимов течения жидкости связано с различными профилями скоростей при данных режимах (рис. 5.2). При ламинарном течении жидкости uср=0,5 umах, а при турбулентном – uср=(0,8…0,95) umах [2, с.55-57; 7, с. 46], поэтому такое различие в значениях α. Следует отметить, что для ламинарного режима величину α можно получить теоретически, используя уравнения параболы и кинетической энергии.
При движении вязкой жидкости, в отличие от идеальной, из-за неравномерного распределения скоростей происходит относительное скольжение слоев или частиц жидкости. Кроме того, во многих случаях происходит вихреобразование и перемешивание жидкости. Все это требует затрат энергии. Поэтому часть энергии, которым обладает поток жидкости, расходуется на преодоление гидравлических сопротивлений и, следовательно, полная энергия потока уменьшается в направлении движения. Строго говоря, потерь энергии не наблюдается, а происходит преобразование части энергии потока в тепловую энергию, которая потом рассеивается в окружающем пространстве. Это преобразование является безвозвратным, поэтому и используется термин «потери полной энергии потока или полного напора».
 Рассмотрим два сечения потока вязкой жидкости 1-1 и 2-2 (рис. 5.3), полные напоры в этих сечениях равны Нср1 и Нср2. Тогда
Рассмотрим два сечения потока вязкой жидкости 1-1 и 2-2 (рис. 5.3), полные напоры в этих сечениях равны Нср1 и Нср2. Тогда
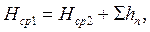 (5.14)
(5.14)
где Σhп – суммарные гидравлические потери полного напора между сечениями1-1 и 2-2.
Используя зависимость для расчета Нср, получим соответствующее уравнение:
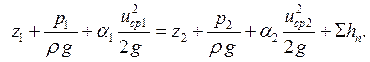 (5.15)
(5.15)
 Полученное уравнение (5.15) является уравнением Бернулли для потока вязкой жидкости. Данное уравнение применимо не только для жидкостей, но и для газов в тех случаях, когда скорость их движения значительно меньше скорости звука [3, с.47].
Полученное уравнение (5.15) является уравнением Бернулли для потока вязкой жидкости. Данное уравнение применимо не только для жидкостей, но и для газов в тех случаях, когда скорость их движения значительно меньше скорости звука [3, с.47].
Графически уравнение Бернулли можно представить соответствующей диаграммой (рис. 5.4). В качестве примера рассмотрим потери напора при течении жидкости по горизонтальному трубопроводу, состоящего из трех участков различного диаметра. В начале трубопровода (сечение А-А) средний полный напор потока равен НсрА. При движении жидкости от сечения А-А к сечению В-В происходит уменьшение полного напора, т.е. линия, характеризующая значение полного напора в любом сечении трубопровода (напорная линия), является падающей. Пьезометрический напор, в отличие от полного, в некоторых случаях может увеличиваться. Например, при внезапном расширении потока и, соответственно, уменьшении скоростного напора hс происходит увеличение пьезометрического напора hпз, т.е. Δhс= u2срА/(2g)- u2срВ/(2g) переходит в пьезометрический напор.
При изменении геодезической высоты потока жидкости происходит изменение геометрического напора hг=z, при этом геометрический напор переходит в пьезометрический напор и обратно. В потерянный напор переходит только пьезометрический напор, причем этот процесс является необратимым:


Уравнение Бернулли применимо не только для жидкостей, но и для газов в тех случаях, когда скорость их движения значительно меньше скорости звука и температура газа по длине не меняется (изотермический процесс)[1, с. 287-290; 3, с.47], т.е. при расчетах вентиляционных воздуховодов, газопроводов низкого давления.
В дальнейшем при проведении анализа физических явлений и процессов, связанных с движению потоков жидкости или газа, будем использовать, как правило, среднюю скорость. Поэтому для упрощения написания формул индекс ср опустим, подразумевая, что буквой u обозначается средняя скорость потока.
Дата добавления: 2015-06-17; просмотров: 1244;
