Теория метода и описание прибора. Основной частью маятника Обербека является крестообразный маховик, который может свободно вращаться вокруг горизонтальной оси (рис

Основной частью маятника Обербека является крестообразный маховик, который может свободно вращаться вокруг горизонтальной оси (рис. 3.2).

На четырех взаимно перпендикулярных стержнях закреплены одинаковые по размеру и массе цилиндрические грузы, положение которых можно менять; при этом изменяется момент инерции маховика.

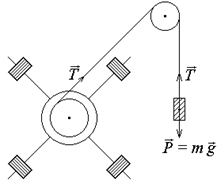Рис. 3.2

На горизонтальной оси маховика имеются два шкива различного диаметра, на один из которых наматывается нить, перекинутая через неподвижный блок. К свободному концу нити подвешивается груз массой m. Сила натяжения нити создает постоянный по величине вращающий момент, под действием которого маховик приводится во вращательное движение. Для экспериментальной проверки основного уравнения

динамики вращательного движения необходимо определить угловое ускорение ε и момент силы M.

Если груз массой m, двигаясь равноускоренно, опускается с высоты h за время t, то ускорение его движения определяется по формуле

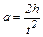. (3.9)

Таким же будет тангенциальное ускорение любой точки на поверхности шкива (при условии, что нить не соскальзывает со шкива), то есть

, (3.10)

где ε – угловое ускорение вращающегося маховика, r – радиус шкива.

Измерив диаметр шкива d, с помощью соотношений (3.9) и (3.10) можно найти угловое ускорение маховика:

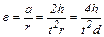. (3.11)

Вращающий момент M, создаваемый силой натяжения нити T, направленной по касательной к шкиву, равен

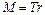. (3.12)

Сила натяжения нити T обусловлена действием на нее груза. В предположении невесомой нити и невесомого блока (через который перекинута нить) сила натяжения постоянна по всей длине нити. Ее можно найти из второго закона Ньютона для опускающегося груза массой m:

.

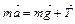В проекции на направление движения ma = mg - T, откуда

T = m (g – a). (3.13)

С учетом того, что r = d/2, и с использованием соотношения (3.9) выражение для вращающегося момента примет вид

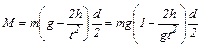. (3.14)

Экспериментальную проверку основного закона динамики вращательного движения можно осуществить следующим образом: при неизменном моменте инерции маховика изучить зависимость его углового ускорения ε от величины вращающего момента M. При этом изменение M можно осуществить изменением массы подвешиваемого груза либо изменением радиуса шкива, на который наматывается нить. Если построить график зависимости ε от M, то экспериментальные точки должны укладываться на прямую, по тангенсу угла наклона α которого можно определить момент инерции маховика. Действительно, поскольку

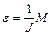, то ,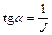

откуда .