РАБОТА 4. ИЗМЕРЕНИЕ СКОРОСТИ ПОЛЕТА ПУЛИ С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО МАЯТНИКА
Цель работы - определить скорость полета пули с помощью крутильных колебаний баллистического маятника.
Теоретические основы лабораторной работы
Скорость полета пули может достигать значительной величины в зависимости от стреляющего устройства. Ее прямое измерение, то есть определение времени, за которое пуля проходит известное расстояние, в учебной лаборатории не представляется возможным.
Для лабораторной работы разработана методика косвенного измерения скорости полета пули с помощью баллистического маятника.
В основе эксперимента лежит явление неупругого соударения тел, в результате которого баллистический маятник совершает крутильные колебания.
Если летящая пуля испытывает неупругий удар с неподвижным телом большей массы, то скорость тела после удара будет существенно меньше первоначальной скорости пули и ее можно будет измерить достаточно простыми методами.
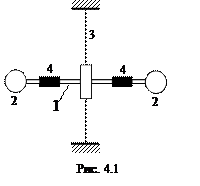 Баллистический маятник представляет собой два стержня 1, подвешенных на вертикально натянутой проволоке 3 (рис. 4.1). На стержнях закреплены мисочки с пластилином 2 и перемещаемые грузы 4. При попадании пули в мисочку с пластилином, маятник начинает поворачиваться вокруг своей вертикальной оси, совершая крутильные колебания.
Баллистический маятник представляет собой два стержня 1, подвешенных на вертикально натянутой проволоке 3 (рис. 4.1). На стержнях закреплены мисочки с пластилином 2 и перемещаемые грузы 4. При попадании пули в мисочку с пластилином, маятник начинает поворачиваться вокруг своей вертикальной оси, совершая крутильные колебания.
При выводе расчётных формул использованы формулы для момента инерции и периода крутильных колебаний физического маятника, а также законы сохранения момента импульса и полной механической энергии. Принято допущение при этом о малости неконсервативных сил.
На основании закона сохранения момента импульса можно написать
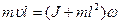 , (4.1)
, (4.1)
где m - масса пули; u - величина скорости пули; l - расстояние от оси вращения маятника до точки удара пули; w - величина угловой скорости маятника; J - момент инерции маятника.
Согласно закону сохранения полной механической энергии при повороте маятника кинетическая энергия маятника переходит в потенциальную энергию закручивающейся проволоки
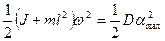 , (4.2)
, (4.2)
где 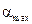 - наибольший угол поворота маятника; D - модуль кручения проволоки.
- наибольший угол поворота маятника; D - модуль кручения проволоки.
Учитывая, что момент инерции пули 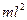 существенно меньше момента инерции маятника J , из уравнений (1) и (2) получим
существенно меньше момента инерции маятника J , из уравнений (1) и (2) получим
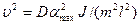 . (4.3)
. (4.3)
Модуль кручения проволоки D можно определить, измерив период крутильных колебаний маятника Т.
При малых углах отклонения период крутильных колебаний маятника определяется по формуле
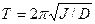 (4.4)
(4.4)
Модуль кручения проволоки
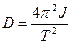 (4.5)
(4.5)
Подставив выражение (4.5) в уравнение (4.3), выразим величину скорости пули
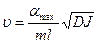 =
= 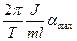 (4.6)
(4.6)
Чтобы исключить измерения момента инерции J, запишем периоды колебаний маятника Т1 и Т2 при различных положениях грузов R1 и R2:
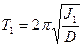
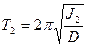 (4.7)
(4.7)
отсюда
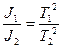 (4.8)
(4.8)
В силу того, что момент инерции величина аддитивная, момент инерции баллистического маятника с грузами выразим в виде суммы
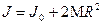 (4.9)
(4.9)
где М - масса двух неподвижных грузов; R - расстояние от центра масс груза до оси вращения; J0 - момент инерции маятника без грузов.
Для различных положений грузов на расстояниях R1 и R2:
в первом положении 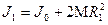 ; во втором положении
; во втором положении
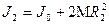
Разность моментов инерции
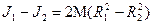 (4.10)
(4.10)
Решая уравнение (8) и (10) относительно J1 найдем
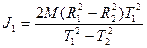 (4.11)
(4.11)
Подставив в формулу (4.6) период T1 и момент инерции J1 для положения грузов на расстоянии R1, получим окончательную формулу для расчета величины скорости пули
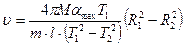 . (12)
. (12)
Описание установки
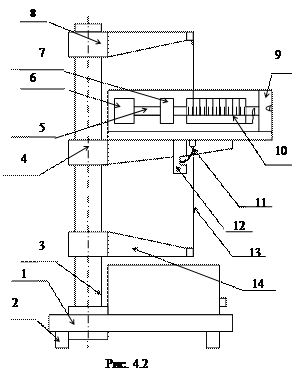 Общий вид установки показан на рис. 4.2. В основании 1, снабженном регулирующими ножками 2, позволяющими выравнивать прибор, закреплена колонка 3 с тремя кронштейнами: верхним 8, средним 4 и нижним 14. К кронштейну 4 прикреплено стреляющее устройство 9, прозрачный экран с нанесенной на него угловой шкалой 10 и фотоэлектрический датчик 12. Кронштейны 4 и 8 имеют зажимы, служащие для крепления стальной проволоки 13, на которой подвешен маятник, состоящий из двух мисочек 6, наполненных пластилином, двух перемещаемых грузов 7, двух стержней 5 и «водилки» 11. Фотоэлектрический датчик соединен разъёмом с привинченным к основанию секундомером.
Общий вид установки показан на рис. 4.2. В основании 1, снабженном регулирующими ножками 2, позволяющими выравнивать прибор, закреплена колонка 3 с тремя кронштейнами: верхним 8, средним 4 и нижним 14. К кронштейну 4 прикреплено стреляющее устройство 9, прозрачный экран с нанесенной на него угловой шкалой 10 и фотоэлектрический датчик 12. Кронштейны 4 и 8 имеют зажимы, служащие для крепления стальной проволоки 13, на которой подвешен маятник, состоящий из двух мисочек 6, наполненных пластилином, двух перемещаемых грузов 7, двух стержней 5 и «водилки» 11. Фотоэлектрический датчик соединен разъёмом с привинченным к основанию секундомером.
Дата добавления: 2015-06-17; просмотров: 1632;
