Дифференциал функции

Пусть функция y=f(x) определена на промежутке Х и дифференцируема в некоторой окрестности точки хÎХ. Тогда существует конечная производная.

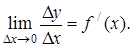
На основании теоремы о связи бесконечно малых величин с пределами функций можно записать

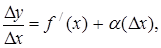
где a(Dх) – бесконечно малая величина при Dх ®0, откуда

Dy=f^/(x)Dx+a(Dх)Dх. (3.5.1)

Таким образом, приращение функции Dу состоит из двух слагаемых: 1) линейного относительно Dх; 2) нелинейного (представляющего бесконечно малую более высокого порядка, чем Dх, ибо

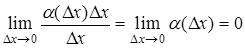Определение. Дифференциалом функции называется главная, линейная относительно Dх часть приращения функции, равная произведению производной на приращение независимой переменной

dy=f^/(x) Dх. (3.5.2)

Пример 32. Найти приращение и дифференциал функции y=2x²–3x при х=10 и Dх=0,1.

Решение. Приращение функции Dy=f(x+Dх)–f(x)=[2(x+Dх)²–3(x+Dх)]– –(2x²–3x)= Dх(4x+2Dх–3).

Дифференциал функции dy=f^/(x)Dх=(4x–3)Dх.

При х=10 и Dх=0,1 имеем Dy=3,72 и dy=3,70. Различие между Dу и dy составляют всего 0,02 или 0,5%.

Пример 33. Найти дифференциал функции х=у.

Решение. dy=dx=x^/×Dх, откуда

dx=Dх,

т. е. дифференциал независимой переменной равен приращению этой переменной.

Поэтому формулу для дифференцирования функции можно записать в виде

dy=f^/(x)dx, (3.5.3)

f^/(x)= 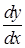. Теперь мы видим, что 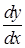не просто символическое обозначение производной, а обычная дробь с числителем dy и знаменателем dx.

Проведем касательную к кривой y=f(x) в точке М, которая образует угол a с положительным направлением оси Ох, т. е. f^/(x)=tg a. Из прямоугольного треугольника MKN KN=MN×tga=Dх tga=f^/(x) Dх, dy=KN. Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y=f(x) в данной точке, когда х получает приращение Dх.

Геометрический смысл дифференциала. Возьмем на графике функции y=f(x) произвольную точку М(х, у). Дадим аргументу х приращение Dх. Тогда функция y=f(x) получит приращение Dy=f(x+Dх)–f(x) (см. рис. 3.25).

y+Dy=f(x+Dх) M₁

Dу

y=f(x) M a dy

a Dх

O x x+Dх x

Рис. 3.25

Дата добавления: 2015-06-17; просмотров: 991;