Группировка неизвестных

Если при расчете симметричной рамы (рис. 8.3 а) выбрана обычная основная система (рис. 8.3 б), то все коэффициенты канонических уравнений

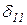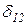X₁+ X₂ +D_1P=0,

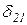X₁+ 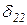X₂ +D_2P=0

будут отличаться от нуля.

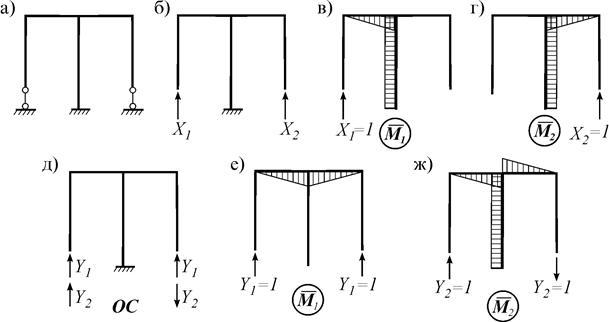
Рис. 8.3

Если же неизвестные группировать по формулам

X₁=Y₁ +Y₂ ,

X₂=Y₁ – Y₂ ,

что соответствует основной системе на рис. 8.3 д, то единичные эпюры (рис. 8.3 е, ж) будут ортогональными ( 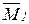Ä 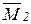=0), и канонические уравнения распадутся на два независимых уравнения:

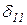Y₁ +D_1P=0,

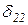Y₂ +D_2P=0.

Как видим, при группировке неизвестных отдельные коэффициенты обращаются в нуль и нет необходимости их вычисления. С другой стороны, распадение системы канонических уравнений на две независимые системы уравнений упрощает их решение. Поэтому группировка неизвестных позволяет существенно уменьшить объем вычислений.