Погрешности измерений. Любой измерительный прибор из-за несовершенства конструкции обладает погрешностью, т.е

Любой измерительный прибор из-за несовершенства конструкции обладает погрешностью, т.е. действительное значение измеряемой величины А_Д отличается от измеренного А_И: А_Д¹А_И.

Величина, равная разности измеренного и действительного значений, называется абсолютной погрешностью измерения и определяется по формуле:

.

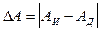Абсолютная погрешность характеризует точность выполненного измерения, но не характеризует точность самого измерительного прибора. Например, если абсолютная погрешность DА измерения силы тока амперметром равна 1 А, то для прибора с пределом измерения 100 А эта величина незначительна, а для прибора с пределом 10 А уже является большой. Таким образом, в своих пределах измерения первый прибор точнее второго.

Для характеристики точности измерительных приборов независимо от их пределов измерения вводится относительная приведенная погрешность измерительного прибора. Величина относительной приведенной погрешности, выраженная в процентах определяет класс точности измерительного прибора:

,

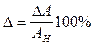где А_Н - номинальное значение шкалы прибора.

Относительная погрешность не зависит от величины измеряемых значений и позволяет оценить точность прибора в любом диапазоне.

Выделяют (в соответствии с ГОСТ) восемь основных классов точности: 4,0; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05. Например, класс точности 1,0 означает, что максимально возможная абсолютная погрешность измерения данным прибором не превышает 1% от его шкалы. Поэтому результат измерения амперметром с пределами шкалы 100 А и классом точности 1,0 силы тока в 15 А может быть записан I=15±1 А. Класс точности указывается на шкале измерительного прибора.

Чем выше класс точности, тем точнее и сложнее (дороже) прибор. Приборы классов 0,05; 0,1; 0,2 применяются для научных исследований, приборы классов 0,5; 1,0; 1,5 - для лабораторных измерений, приборы классов 2,5; 4,0 - щитовые приборы - для грубых измерений.