Векторные диаграммы. Производить операции умножения, сложения и т.п

Производить операции умножения, сложения и т.п. с токами и напряжениями, изображенными в виде волновых диаграмм, неудобно. Поэтому на практике синусоидальные величины представляют в виде векторов, а затем указанные операции производят с ними. Это значительно упрощает расчеты и делает их более наглядными.

Представление синусоиды в виде волновой диаграммы и вращающегося вектора показано на рисунке.

Вращая вектор I против часовой стрелки его конец будет описывать окружность. При вращении вектора с частотой w его проекция на вертикальную ось изменяется по синусоидальному закону и равна мгновенному значению синусоиды в соответствующие моменты времени. Хорошо видны следующие аналогии:

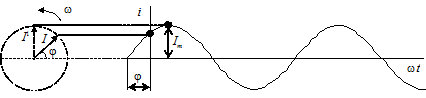
− длина вектора равна амплитуде синусоиды;

− угол между горизонтальной осью и вектором равен начальной фазе синусоиды.

В электротехнике векторы изображают не вращающимися, а неподвижными, для момента времени t=0 . Часто масштабы векторов выбирают так, чтобы длина вектора соответствовала не амплитуде, а действующему значению. Угол наклона к оси абсцисс равен начальной фазе. Учитываемые параметры (действующее значение и начальная фаза) полностью определяют синусоидальную функцию и позволяют для любого вектора восстановить ее и наоборот.

Так можно представить целую совокупность различных величин u, i, e. Если эти величины одинаковой частоты, то их совокупность представляет собой векторную диаграмму.

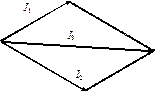
На рисунке для примера представлена совокупность векторов I₁ и I₂, а также результирующий вектор I₃, определяемый их суммой. Угол измеренный между векторами называют углом сдвига фаз. Если угол между двумя векторами равен нулю, то говорят, что они совпадают по фазе. Если угол равен 180°, то говорят, что векторы находятся в противофазе.