Расчет вязкости по методу М. В. Охотина 2 страница
 Твердость является свойством материала сопротивляться деформации или разрушению поверхностного слоя, представляет собой разновидность прочности, характеризует прочность поверхностного слоя при вдавливании. Критерием прочности при вдавливании является предел упругости, превышение которого ведет к разрушению твердого тела или к пластической деформации.
Твердость является свойством материала сопротивляться деформации или разрушению поверхностного слоя, представляет собой разновидность прочности, характеризует прочность поверхностного слоя при вдавливании. Критерием прочности при вдавливании является предел упругости, превышение которого ведет к разрушению твердого тела или к пластической деформации.
Твердость зависит от прочности химических связей материала. Твердость стекла определяет его сопротивление царапанию, абразивоустойчивость, скорость и режимы процессов шлифования, полирования, сверления, резания.
Твердость количественно характеризуют с помощью одного из методов: вдавливания в образец индентора (статическая твердость), деформации при динамической нагрузке (динамическая твердость), царапания или истирания абразивом. Единого общепризнанного способа количественного определения твердости стекол не существует. Наиболее распространены следующие способы испытаний твердости на статическое вдавливание индентора: способ Бринелля (предусматривает вдавливание стального шарика диаметром 1 мм); способ Виккерса (вдавливание алмазной пирамиды с углом у вершины, равным 136 º); вдавливание алмазной пирамиды асимметричной формы, образующей отпечаток в виде параллелограмма (способ Кнупа для испытания особо твердых материалов); вдавливание стального шарика (в случае мягких материалов) или алмазного конуса с полусферической вершиной (для твердых материалов, способ Роквелла). В первых трех случаях твердость выражается как нагрузка, отнесенная к площади отпечатка (Н/м2). В способе Роквелла твердость определяют по разности глубин отпечатков при различных значениях нагрузки.
Значения твердости типичных промышленных стекол приведены в табл. 2.7. К числу твердых относятся кварцевое стекло, малощелочные боросиликатные стекла с содержанием В2О3 до 10-12 %, алюмосиликатные стекла с высоким содержанием Al2O3.
С повышением содержания щелочных оксидов в составе стекла снижается их твердость. Наиболее мягкими являются многосвинцовые силикатные стекла типа тяжелых флинтов. Твердые стекла, как правило, обладают повышенной химической устойчивостью к действию воды и водных растворов минеральных кислот (кроме плавиковой и фосфорных).
 Прочность характеризует свойство материалов сопротивляться разрушению при воздействии внешних нагрузок. Мерой прочности является предел прочности – максимальное напряжение, вызывающее разрушение материала под действием статической нагрузки. В зависимости от вида действующей нагрузки различают пределы прочности при растяжении, сжатии, изгибе, кручении, ударе и т. д. Прочность стекол на изгиб изменяется (в зависимости от состава) в пределах от 0,03 до 0,12 ГПа, на сжатие – от 0,5 до 2,5 ГПа.
Прочность характеризует свойство материалов сопротивляться разрушению при воздействии внешних нагрузок. Мерой прочности является предел прочности – максимальное напряжение, вызывающее разрушение материала под действием статической нагрузки. В зависимости от вида действующей нагрузки различают пределы прочности при растяжении, сжатии, изгибе, кручении, ударе и т. д. Прочность стекол на изгиб изменяется (в зависимости от состава) в пределах от 0,03 до 0,12 ГПа, на сжатие – от 0,5 до 2,5 ГПа.
 Изделия из стекла способны выдерживать гораздо более высокие напряжения на сжатие, чем на растяжение.
Изделия из стекла способны выдерживать гораздо более высокие напряжения на сжатие, чем на растяжение.
 Техническая и теоретическая прочности стекол. Техническая прочность характеризует прочность реальных изделий. Теоретическая прочность является расчетной величиной для идеального бездефектного гомогенного материала, нагружаемого квазистатично при достаточно низких температурах. Теоретическая прочность является физически определенной величиной и во многом зависит от природы и прочности химических связей в веществе.
Техническая и теоретическая прочности стекол. Техническая прочность характеризует прочность реальных изделий. Теоретическая прочность является расчетной величиной для идеального бездефектного гомогенного материала, нагружаемого квазистатично при достаточно низких температурах. Теоретическая прочность является физически определенной величиной и во многом зависит от природы и прочности химических связей в веществе.
Для ориентировочного расчета теоретической прочности были предложены уравнения, устанавливающие связь между σтеор и модулем Юнга. Например, согласно уравнению Орована, для случая одноосного растяжения σтеор = (0,1-0,2)Е. Зная модуль Юнга, на основании этого уравнения можно ориентировочно оценить σтеор, которая оказывается равной 7-18 ГПа.
Сопоставление теоретической прочности с реальной технической прочностью показывает, что они отличаются друг от друга на 3-4 порядка, особенно низки по сравнению с теоретической реальные прочности на изгиб и на растяжение. Большинство известных материалов имеют техническую прочность более низкую, чем теоретическую.
 Теория прочности Гриффитса (1920 г.) объясняет расхождение значений теоретической и технической прочности твердых тел наличием на их поверхности большого числа микродефектов, названных «трещинами Гриффитса». Микротрещины по Гриффитсу представляют собой локальные нарушения целостности поверхностного слоя. Они могут быть обусловлены разрывом химических связей Si–О–Si в результате: а) абразивного действия твердых частиц (даже частиц пыли) или контакта с поверхностями твердых тел; б) химического взаимодействия с влагой и газами воздуха.
Теория прочности Гриффитса (1920 г.) объясняет расхождение значений теоретической и технической прочности твердых тел наличием на их поверхности большого числа микродефектов, названных «трещинами Гриффитса». Микротрещины по Гриффитсу представляют собой локальные нарушения целостности поверхностного слоя. Они могут быть обусловлены разрывом химических связей Si–О–Si в результате: а) абразивного действия твердых частиц (даже частиц пыли) или контакта с поверхностями твердых тел; б) химического взаимодействия с влагой и газами воздуха.
Схематически трещина по Гриффитсу может быть изображена в виде щели с эллиптическим закруглением в вершине (рис. 2.4).
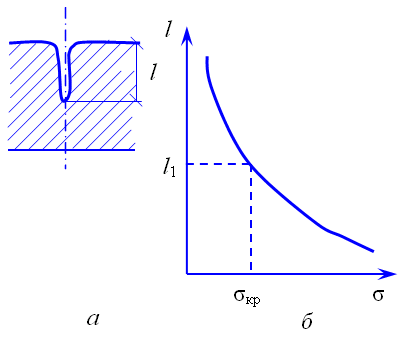
Рис. 2.4. Модель микротрещины по Гриффитсу (а) и зависимость длины трещины от действующих напряжений (б)
Наличие микродефектов в поверхностном слое вызывает резкое снижение прочности материала. Исходя из закона сохранения энергии, Гриффитс установил зависимость длины трещины l от приложенного напряжения σ в виде соотношения  . В случае хрупкого разрушения С является постоянной величиной и может быть рассчитана, исходя из физико-механических свойств материала по формуле
. В случае хрупкого разрушения С является постоянной величиной и может быть рассчитана, исходя из физико-механических свойств материала по формуле
С = (2Еσп/πμ)1/2, (2.10)
где Е – модуль Юнга;
σ – поверхностное натяжение;
μ – коэффициент Пуассона.
Соотношение Гриффитса позволяет выделить области напряжений, которые не будут вызывать увеличения длины трещины, пока напряжение не достигнет некоторого критического значения σкр. Трещины с начальной длиной l1 не будут расти при действии напряжений, меньших σкр. При напряжениях, превышающих σкр, трещины будут развиваться, что приведет к разрушению стекла. Величина σкр служит важнейшей характеристикой сопротивления материала росту трещин. Наиболее опасны крупные трещины, поскольку им соответствуют минимальные значения σкр. Согласно Гриффитсу, трещина является сильным концентратором напряжений. В вершинах трещины возникают напряжения, значительно превышающие приложенное напряжение и близкие к теоретической прочности стекла.
Для расчета коэффициента концентрации напряжений в вершине трещины (σ2) Гриффитс использовал уравнение, которое позволяет связать σ2 с приложенным напряжением σ1, длиной трещины l и радиусом кривизны в вершине трещины ρ:
 (2.11)
(2.11)
Механизм разрушения стекла включает две последовательные стадии: 1) рост наиболее опасной трещины; 2) возникновение и одновременный рост большого числа вторичных трещин.
На первой стадии рост наиболее опасной (крупной) трещины, расположенной перпендикулярно направлению действия приложенной нагрузки, начинается при значениях σ2, превышающих σкр. Прочность образца на этой стадии определяется отношением действующей силы к площади сечения образца за вычетом площади, на которую распространилась трещина. При достижении трещиной некоторого критического значения длины, когда истинное сечение образца становится малым, а напряжение в вершине трещины приближается к значению теоретической прочности, наступает вторая стадия разрушения. На второй стадии разрушения возникает большое число вторичных трещин, которые растут с высокой скоростью (порядка 5000 м/с).
Встречаясь с крупной первой трещиной и друг с другом, они образуют многочисленные линии сколов. Сетка линий сколов в макроскопическом масштабе дает шероховато-раковистую поверхность. В изломе образца можно наблюдать две зоны, соответствующие стадиям разрушения: зону зеркальной поверхности, обусловленную ростом одной трещины; зону шероховато-раковистой поверхности, обусловленную ростом большого числа трещин. Зарождению и развитию микротрещин на поверхности способствуют загрязнение поверхности изделий, контакт ее с твердыми поверхностями, образование напряжений при неравномерном охлаждении стекол, наличие включений в стекломассе и ее неоднородность, влажность окружающей среды.
 Согласно статистической теории прочности поверхностные слои отличаются по прочности от внутренних слоев: прочность поверхностных слоев меньше прочности объема, как следствие существования на поверхности дефектного слоя. Распределение дефектов на поверхности, особенно опасных, является статистически произвольным и может быть оценено вероятностной функцией распределения. Предел прочности стекол, в силу указанной особенности, также является величиной статистической. Для количественной характеристики предела прочности необходимо знать среднее значение σ из n измерений и доверительный вероятностный интервал значений Δσ. В отличие от плотности и показателя преломления предел прочности не является константой вещества. Статистически достоверное число испытаний для оценки прочности лежит в интервале значений 10-100. Предел прочности зависит от степени дефектности поверхностного слоя, от статистики распределения микротрещин. На рис. 2.5 приведены кривые распределения значений предела прочности для образцов листового стекла, отличающихся состоянием поверхности и условиями испытания прочности. Функция распределения f(σ) характеризует повторяемость результатов из N числа измерений и определяется по формуле
Согласно статистической теории прочности поверхностные слои отличаются по прочности от внутренних слоев: прочность поверхностных слоев меньше прочности объема, как следствие существования на поверхности дефектного слоя. Распределение дефектов на поверхности, особенно опасных, является статистически произвольным и может быть оценено вероятностной функцией распределения. Предел прочности стекол, в силу указанной особенности, также является величиной статистической. Для количественной характеристики предела прочности необходимо знать среднее значение σ из n измерений и доверительный вероятностный интервал значений Δσ. В отличие от плотности и показателя преломления предел прочности не является константой вещества. Статистически достоверное число испытаний для оценки прочности лежит в интервале значений 10-100. Предел прочности зависит от степени дефектности поверхностного слоя, от статистики распределения микротрещин. На рис. 2.5 приведены кривые распределения значений предела прочности для образцов листового стекла, отличающихся состоянием поверхности и условиями испытания прочности. Функция распределения f(σ) характеризует повторяемость результатов из N числа измерений и определяется по формуле
f(σ) = (1/N)(ΔN/Δσ), (2.12)
где N – число образцов с прочностью в интервале значений от σ до σ + Δσ (интервал прочности Δσ определяют методом приближения).
Кривая 1 (рис. 2.5) характеризует функцию распределения предела прочности для плоских образцов листового стекла с поврежденными в результате резки алмазом краями. Значения прочности стекла минимальны, разброс результатов испытания небольшой. Видимо, в процессе резания алмазом, а также при шлифовке и полировке изделий образуются предельно опасные дефекты краев. Низкий разброс значений позволяет заключить, что края образцов имеют дефекты примерно одинаковой степени опасности. Кривая 2 характеризует прочность плоских образцов листового стекла с неповрежденными краями. Среднее значение прочности оказывается более высоким, в то время как разброс значений прочности растет. Это означает, что имеются образцы как с опасными, так и неопасными дефектами. Кривая 3 показывает изменение прочности поверхности плоских образцов листового стекла. Среднее значение предела прочности в данном случае максимально. Большой разброс значений свидетельствует, что поверхность стекла содержит широкий набор различных по степени опасности дефектов.

Рис. 2.5. Экспериментальные кривые распределения прочности на поперечный изгиб листового стекла
Статистическая теория прочности устанавливает также зависимость между объемом напряженной части образца и площадью его поверхности («масштабный фактор»). Чем больше объем напряженной части образца, тем ниже прочность. Образцы с развитой поверхностью содержат большее число опасных дефектов.
 Флуктуационная теория прочности. Получение высокопрочных стекол ставит ряд вопросов, касающихся механизма и кинетики разрушения бездефектных материалов. Согласно флуктуационной гипотезе Марша прочность бездефектных стеклянных волокон определяется пределом текучести. Стекла в высокопрочном состоянии являются пластичными материалами, предел текучести которых может быть найден из соотношения σт = 0,055Е. Появление остаточных (неупругих) деформаций в стекле инициирует появление микротрещин, их рост и разрушение изделия. Теоретическая прочность стекла выше предела текучести, в то время как предел текучести выше хрупкой прочности стекла. Механизм роста трещин состоит в последовательном разрыве связей в вершине под действием напряжений и флуктуации тепловых колебаний частиц.
Флуктуационная теория прочности. Получение высокопрочных стекол ставит ряд вопросов, касающихся механизма и кинетики разрушения бездефектных материалов. Согласно флуктуационной гипотезе Марша прочность бездефектных стеклянных волокон определяется пределом текучести. Стекла в высокопрочном состоянии являются пластичными материалами, предел текучести которых может быть найден из соотношения σт = 0,055Е. Появление остаточных (неупругих) деформаций в стекле инициирует появление микротрещин, их рост и разрушение изделия. Теоретическая прочность стекла выше предела текучести, в то время как предел текучести выше хрупкой прочности стекла. Механизм роста трещин состоит в последовательном разрыве связей в вершине под действием напряжений и флуктуации тепловых колебаний частиц.
Расчет предела прочности стекла при сжатии
Предел прочности при сжатии стекла можно определить расчетным путем, исходя из его химического состава, по правилу аддитивности с достаточной для практических целей точностью (около 25-30 %). Расчет ведут по формуле
Rсж = Р1·Rсж.1 + Р2·Rсж.2 + … + Рn · Rсж.n, (2.13)
где Р1, Р2, … , Рn – содержание в стекле каждого из оксидов в мас. %;
Rсж.1, Rсж.2, … , Rсж.n – удельные прочностные коэффициенты соответствующих оксидов в стекле (табл. 2.8).
Таблица 2.8
Коэффициенты для расчета предела прочности стекол при сжатии
| Оксиды | Коэффициент | Оксиды | Коэффициент |
| SiO2 | 1,23 | BaO | 0,62 |
| B2O3 | 0,90 | ZnO | 0,60 |
| P2O5 | 0,76 | PbO | 0,48 |
| Al2O3 | 1,00 | Na2O | 0,60 |
| CaO | 0,20 | K2O | 0,05 |
| MgO | 1,10 |
Расчет предела прочности стекла при растяжении
Сопротивление стекла разрыву определяют расчетом по правилу аддитивности с точностью около 20-25 % по формуле
Rсж = Р1 · Rр.1 + Р2 · Rр.2 + … + Рn·Rр.n , (2.14)
где Р1, Р2, … , Рn – содержание в стекле каждого из оксидов в мас. %;
Rр.1, Rр.2, … , Rр.n – удельные прочностные константы соответствующих оксидов в стекле (табл. 2.9).
Таблица 2.9
Константы для расчета предела прочности стекол при растяжении (по Винкельману и Шотту)
| Оксиды | Коэффициент | Оксиды | Коэффициент |
| SiO2 | 0,090 | BaO | 0,050 |
| B2O3 | 0,065 | ZnO | 0,150 |
| P2O5 | 0,075 | PbO | 0,025 |
| Al2O3 | 0,050 | Na2O | 0,020 |
| CaO | 0,200 | As2O5 | 0,030 |
| MgO | 0,010 |
Расчет модуля упругости и модуля сдвига
Модули упругости и сдвига стекла могут быть рассчитаны по правилу аддитивности. Однако следует помнить, что математическая зависимость модуля от химического состава стекла в действительности значительно сложнее, чем это выражено в формуле, поэтому данные, получаемые расчетным путем, являются ориентировочными.
Для расчета модуля упругости и модуля сдвига по методу А. А. Аппена используют уравнение (2.15) или (2.16):
K = Σ Ni k/i / Σ Ni, (2.15)
где K – расчетная величина свойства;
Ni – содержание оксидов в стекле, мол. %;
k/i – приближенно-усредненная величина этого свойства для каждого компонента, принимаемая по табличным данным .
Приближенно-усредненные парциальные величины для SiO2 не являются постоянными и могут быть определены при помощи следующих простых уравнений:
модуль упругости E/SiO2 · 10-3 = 6,5 + 0,02 (NSiO2 – 67);
модуль сдвига G/SiO2 · 10-3 = 2,7 + 0,01 (NSiO2 – 67).
В этих уравнениях NSiO2 выражают в молярных процентах. При NSiO2 < 67 значения соответствующих величин принимают постоянными: ESiO2 · 10-3 = 6,5; GSiO2 · 10-3 = 2,7;
Е = Р1 · Е1 + Р2 · Е2 + … + Рn · Еn, (2.16)
где Р1, Р2, … , Рn – содержание в стекле каждого из оксидов в мас. %;
Eр.1, Eр.2, … , En – удельные константы упругости соответствующих оксидов в стекле (табл. 2.10).
Пример. Определить по Аппену модуль упругости стекла следующего состава (мас. %): SiO2 – 73; Al2O3 – 1; CaO – 10; Na2O – 13; MgO – 3.
| Состав стекла в молях: | SiO2 | 73/60,06 = 1,2154; |
| Al2O3 | 1/101,9 = 0,0098; | |
| CaO | 10/56 = 0,1786; | |
| Na2O | 13/62 = 0,2097; | |
| MgO | 3/40,3 = 0,0744. |
Всего будет 1,6879 моль. Определяем содержание SiO2 в молекулярных процентах: NSiO2 = (1,2154 · 100)/1,6879 = 72, так как NSiO2 > 67, принимаем RSiO2 = 70, отсюда Е = 73 · 70 + 1 · 180 + 10 · 70 + 13 · 61 + 3 · 0 = 6783.
Таблица 2.10
Константы для расчета упругости стекол
| Оксиды | Значение констант для стекол | Оксиды | Значение констант для стекол | ||||
| не содержащих В2О3 | не содержащих РbO, но содержащих В2О3 | содержащих В2О3, Р2О5, PbO | не содержащих В2О3 | не содержащих РbO, но содержащих В2О3 | содержащих В2О3, Р2О5, PbO | ||
| SiO2 | MgO | – | |||||
| B2O3 | – | BaO | – | ||||
| As2O5 | ZnO | – | |||||
| P2O5 | – | – | PbO | – | |||
| Al2O3 | Na2O | ||||||
| CaO | – | K2O |
2.5. Электрические свойства стекол
Группу электрических свойств составляют электропроводность, электрическое сопротивление, диэлектрическая проницаемость, диэлектрические потери, электрическая прочность. В зависимости от состава и от температуры окружающей среды стекла могут быть изоляторами (диэлектриками), полупроводниками и проводниками тока.
Стекла применяют для изготовления низко- и высоковольтных изоляторов, баллонов и ножек осветительных и электронных ламп, газоразрядных приборов, тонко- и толстостенных газонепроницаемых и вакуум-плотных оболочек, различных электровакуумных приборов, рентгеновских трубок, компонентов электрических цепей, обладающих специфическими электрофизическими свойствами, и других приборов.
 Электропроводность характеризует способность материала проводить электрический ток под действием электрического поля. Мерой электропроводности является удельная объемная электропроводность (χ, Ом-1·м-1), равная отношению плотности тока проводимости к напряженности электрического поля. В общем случае электропроводность обусловлена направленным перемещением зарядов и равна произведению заряда носителей тока на их концентрацию и подвижность.
Электропроводность характеризует способность материала проводить электрический ток под действием электрического поля. Мерой электропроводности является удельная объемная электропроводность (χ, Ом-1·м-1), равная отношению плотности тока проводимости к напряженности электрического поля. В общем случае электропроводность обусловлена направленным перемещением зарядов и равна произведению заряда носителей тока на их концентрацию и подвижность.
Единица размерности удельной электропроводности может быть представлена также в виде Сим·м-1, где Сим (Сименс) характеризует электрическую проводимость материала сопротивлением 1 Ом.
Удельная объемная электропроводность и удельное объемное сопротивление связаны соотношением χ = 1/ρ. Удельное сопротивление определяют из соотношения
ρ = R(S / l), (2.17)
где R – сопротивление;
S – площадь поперечного сечения;
l – длина слоя.
Удельная поверхностная электропроводность χS характеризует способность поверхностного слоя переносить заряд. Она определяется проводимостью квадрата поверхностного слоя со стороной 1 м, к противоположным сторонам которого приложено напряжение 1 В. Поверхностная электропроводность может существенно отличаться от объемной из-за присутствия на поверхности адсорбированной влаги, продуктов гидролиза и т. п.
По удельной объемной электропроводности при комнатной температуре материалы делят на три класса: проводники (χ = l06–l010 Ом-1·м-1); полупроводники (χ = 106–l0-8·Ом-1·м-1); изоляторы (χ = 10-8–10-19 Ом-1·м-1). Большая группа оксидных стекол, включая силикатные, боратные, фосфатные и другие, принадлежит к классу изоляторов, что обусловлено высокими значениями ширины запрещенной зоны. При комнатной температуре удельная объемная электропроводность силикатных стекол, например, лежит в пределах 10-7–10-15 Ом-1·м-1. Установлено, что носителями тока в кислородных стеклах являются катионы щелочных или щелочноземельных металлов.
Низкая электропроводность оксидных стекол обусловлена малой подвижностью катионов. Повышение температуры сопровождается снижением вязкости, увеличением подвижности носителей тока, в результате чего электропроводность возрастает на несколько порядков.
Влияние химического состава на электропроводность стекол. Электропроводность силикатных стекол зависит в первую очередь от концентрации щелочных компонентов и от их подвижности. Кварцевое стекло является почти идеальным изолятором в серии силикатных стекол. Его электропроводность при комнатной температуре равна 10-18 Ом-1·м-1, а при 800 ºС – 10-4 Ом-1·м-1.
 Электропроводность натриевосиликатных стекол растет по мере увеличения концентрации оксида натрия в области как низких, так и высоких температур. Введение ионов кальция, бария, свинца снижает подвижность ионов натрия и тем самым электропроводность стекла. По влиянию на электропроводность натриевосиликатных стекол оксиды металлов можно расположить в следующий ряд: СаО–(В2О3–ВаО– Fе2O3–РЬО–MgO–ZnO)–SiO2–Al2O3–K2O–Li2O–Na2O. Наиболее резко снижает электропроводность СаО.
Электропроводность натриевосиликатных стекол растет по мере увеличения концентрации оксида натрия в области как низких, так и высоких температур. Введение ионов кальция, бария, свинца снижает подвижность ионов натрия и тем самым электропроводность стекла. По влиянию на электропроводность натриевосиликатных стекол оксиды металлов можно расположить в следующий ряд: СаО–(В2О3–ВаО– Fе2O3–РЬО–MgO–ZnO)–SiO2–Al2O3–K2O–Li2O–Na2O. Наиболее резко снижает электропроводность СаО.
При одновременном присутствии в составе стекла двух типов катионов щелочных металлов электропроводность стекол резко снижается по сравнению с электропроводностью стекол соответствующих бинарных систем (рис. 2.6).

Рис. 2.6. Полищелочной эффект в стеклах систем при 150 ºС:
1 – (Na, K)2O–SiO2;
2 – (Li, Na)2O–SiO2;
3 – (Li, K)2O–SiO2
Минимальная электропроводность соответствует равному соотношению мольных долей каждого оксида щелочного металла. Наблюдаемый эффект изменения электропроводности, при одновременном присутствии двух щелочных компонентов, имеет следующие названия: «эффект двух щелочей«, «эффект нейтрализации», «полищелочной эффект». Природа явления состоит в том, что разнородные атомы щелочных элементов заполняют различные координационные полости в структурной сетке, компактность упаковки сетки растет, снижается число свободных полостей и подвижность катионов. В бесщелочных силикатных стеклах электропроводность обусловлена перемещением катионов щелочноземельных металлов. Повышение их концентрации способствует повышению электропроводности.
Влияние температуры на электропроводность силикатных стекол. Повышение температуры способствует резкому увеличению электропроводности (рис. 2.7). Зависимость электропроводности от температуры в широком температурном интервале может быть описана уравнением
χ = А е-Еχ/RT, (2.18)
где Еχ – энергия активации электропроводности;
А – константа.
Энергия активации электропроводности характеризует потенциальный барьер, который необходимо преодолеть катионам при перемещении в направлении электрического поля. Энергия активации электропроводности не зависит от температурной области (от комнатной до температуры стеклования), и ее среднее значение для обычных силикатных стекол составляет примерно 0-90 кДж/моль.
Зависимость электропроводности от температуры в том интервале температур имеет четко выраженный экспоненциальный характер, что подтверждается соответствием экспериментальных данных линейной зависимости типа  . В интервале стеклования ход зависимости χ = f(T) усложняется. На графике lnχ – (1/Т) экспериментальные данные укладываются на S-образную кривую. Энергия активации электропроводности в области температур выше Tg зависит от температуры и уменьшается обратно пропорционально последней. В расплавах зависимость электропроводности от температуры описывается экспонентой, но значения константы А и величины Еχ отличаются от таковых, характерных для твердого состояния.
. В интервале стеклования ход зависимости χ = f(T) усложняется. На графике lnχ – (1/Т) экспериментальные данные укладываются на S-образную кривую. Энергия активации электропроводности в области температур выше Tg зависит от температуры и уменьшается обратно пропорционально последней. В расплавах зависимость электропроводности от температуры описывается экспонентой, но значения константы А и величины Еχ отличаются от таковых, характерных для твердого состояния.
Электропроводность стекол зависит от степени неравновесности состояния, т. е. электропроводность закаленных стекол выше электропроводности тех же стекол после отжига. Закаленные стекла имеют больший молярный объем (и меньшую плотность), что облегчает миграцию катионов. После отжига стекла структурная сетка уплотняется и электропроводность стекла снижается.
Электропроводность стекол с различной степенью закалки показана на рис. 2.7 (кривые вг и в/г/).
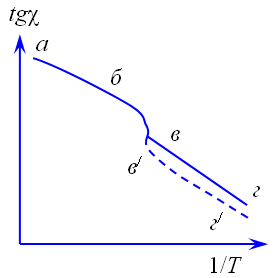
Рис. 2.7. Зависимость электропроводности стекол от температуры: аб – расплав; бв – пластичное; вг и в/г/ – твердое состояние
Изменение удельной электропроводности в зависимости от температуры характеризуют температурным коэффициентом ТКχ, который определяют из соотношения
ТКχ = (1/χ) (dχ /dT). (2.19)
На практике пригодность стекла для работы в тех или иных температурных условиях оценивают по температуре ТК100, при которой стекло имеет удельную электропроводность 100·10-8 Ом-1·м-1. Эта температура зависит от химического состава стекла (табл. 2.11).
Таблица 2.11
Электрические свойства электротехнических стекол (при 20 ºС)
| Марка стекла | TK100 ºС | ε (f = 106 Гц) | tgδ·104 | Eпр, кВ/м ·10-3 |
| С-5-1 (кварцевое) | 3,81 | |||
| П-15 (пирекс) | – | – | – | |
| С 38-1 (ЗС-9) | 4,8 | |||
| С 48-3 | 6,95 | – |
Поверхностная электропроводность стекол. В результате адсорбции влаги, а также продуктов химического взаимодействия поверхности с влагой воздуха на поверхности изделий создается электропроводящий слой. Во многих случаях этот процесс является нежелательным, т. к. отрицательно сказывается на изоляционных свойствах стекла.
Дата добавления: 2015-06-17; просмотров: 1120;
