5 страница. Мощность Ni, развиваемую силами приложенными к i-му звену, представим

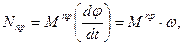
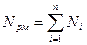(8)

Мощность N_i, развиваемую силами приложенными к i-му звену, представим

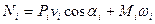(9)

Где P_i – сила, действующая на i-е звено, v_i – скорость точки приложения силы P_i, α_i – угол между ними; M_i – момент сил, действующий на i-е звено. Подставляя (7), (8), (9) в (6) находим

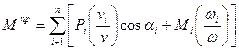
В общем случае из (10) следует, что M^пр является функцией положения (φ) и P_i и M_i , которые, в свою очередь, являются функциями t; φ; ω т.е. М^пр=f(φ,ω,t)

Аналогично получим приведенную движущую силу или силу сопротивления

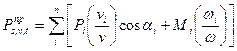
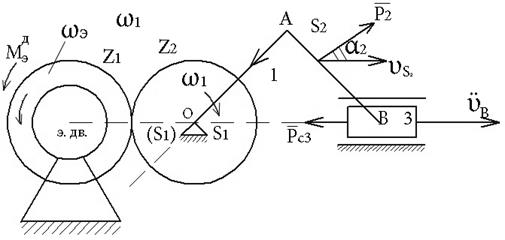
В качестве примера рассмотрим простейший машинный агрегат , где за звено приведения примем кривошип 1, учитывая (4) получим:

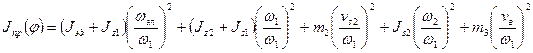, где

J_эд, J_z1, J_z2, J_s1, J_s2 – моменты инерции ротора эд.дв., зубчатых колес z₁, z₂,

Звенья 1,2 относит. Центров тяжести; m₂,m₃ – массы 2,3 звеньев, точка S₁ совпадает с O

Учитывая (10) имеем:

(движущих сил)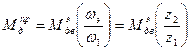

сил сопротивления

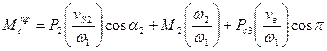
Основные формы уравнений движения и их анализ

Положим, что МА представлен в виде 1-ой динамической модели. Для вывода уравнений движения зв. Пр. можно воспользоваться уравнением Лагранжа 2 рода или теоремой об изменении кинетической энергии механической системы

Во втором случае будут более простые выкладки

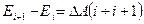(11)

Где E_i, E_i+1 - кинетическая энергия системы в положении i и (i+1)

∆A - работа внешних сил на перемещение при изменении положения системы от i к (i+1). В зависимости от конкретного представления E и ∆A различают две формы уравнений движения интегральную и дифференциальную

Для интегральной формы:

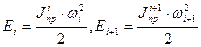
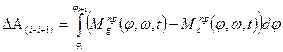(12)

Подставляя (12) в (11) получим интегральную форму уравнения движения МА при моделировании его кривошипом

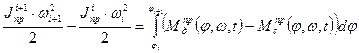(13)

Где интегралы означают, соответственно, работу (приведенную) движущих сил и сил сопротивления.

Для дифференциальной формы:

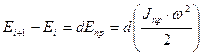
	(14)

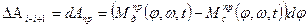
Подставляя (14) в (11) и дифференцируя его по φ получим два вида дифференциальных уравнений движения МА при моделировании его кривошипом

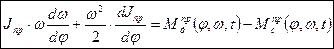(15)

Или учтя, что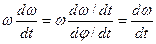

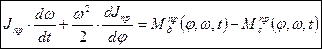(16)

Если мы моделируем МА второй моделью то в уравнениях (13), (15), (16) следует заменить J на m, а M на P.

Уравнение движения в интегральной форме используют, как правило, когда приведенная функция J_пр, 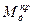, 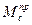в графическом виде. При этом интегрировании уравнения также ведется один из графических методов

Уравнение движения в дифференциальной форме используется при задании приведенной функций (J_пр, 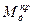, 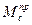) в аналитическом виде. Интегрирование уравнения осуществляется при помощи одного из численных методов решения (интегрирования) нелинейных дифференциальных уравнений на ЭВМ.

Методы решения уравнений движения МА.

В зависимости от формы задания приведенных функций (графической или аналитической) и аргументов от которых зависят эти функции, для решения дифференциальных уравнений движения используются различные методы.

Если приведенные силовые функци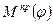и или 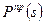зависят только от положения и заданы в графическом виде то для решения широко используют графический метод Виттенбауэра (метод с использованием диаграмм энергомасс ) в различных модификациях. Такая задача характерна при исследовании движения различного рода гидромашин, пневмоустройств и т.п.Если приведенные силовые функции зависят не только от положения, но и от угловой скорости и заданы в графическом виде, что характерно для многих машин с электродвигателем, то в расчетной практике используют графоаналитический метод Виттенбауэра в различных модификациях.

Из аналитических методов, которые пригодны при любой форме и законе задания приведенных силовых функций наиболее широкое применение имеют метод конечных разностей (предложен Барановым) и метод Рунге-Кутта в различных модификациях.

Рассмотрим некоторые из них.

Метод Виттенбауэра (диаграммы энергомасс )

Сущность его состоит в следующем:

Предположим задано уравнение движения звена приведения соверщающего вращательное движение, в интегральной форме в виде

=>

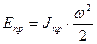
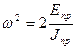(17)

Построив график зависимости 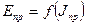на основании (17) можно найти угловую скорость входного звена машины ω_i в каждом i-ом положении, т.е. закон движения ω_i = f(φ_i). Такой график получил название диаграммы энергомасс или Виттенбаэура. (аналогично можно сделать и для звена совершающего поступательное движение). Поскольку, как выше отмечалось, в данном случае 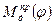и 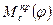– функции только положения, то построить диаграмму достаточно просто. Рассмотрим как это делается на примере 1-ой модели.

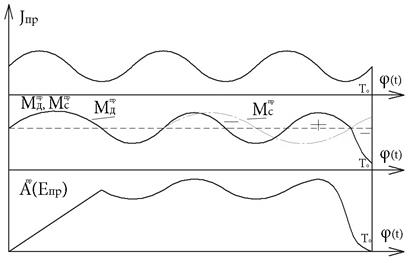
Пусть 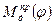; ; 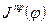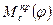заданы в виде графиков, где T_o – время работы машины. Интегрируя график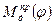и и 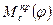можно определить соответствующие работы 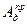; 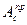. Работа определяется по графику (в) , либо

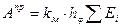
В соответствии с теоремой об изменении кинетической энергии зависимость 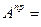f(φ) численно равна изменению кинетической энергии E_пр = f(φ).

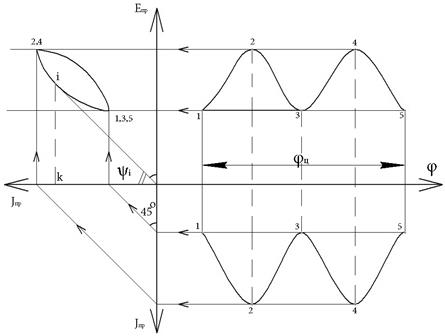
Исключая независимую величину φ из графиков J_пр = f(φ) и E_пр = f(φ)

Строим диаграмму энергомасс (для простоты выполнения для одного цикла)

работы машины φ_ц

kφ = …. 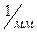kE = …. 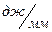kJ = ….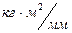

Возьмем произвольную точку i на диаграмме и соединим с началом координат. Определим tgψ_i

tgψ_i = 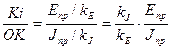(18)

Выразив из (18) 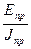подставим в (17) получим

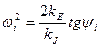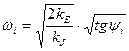или (19)

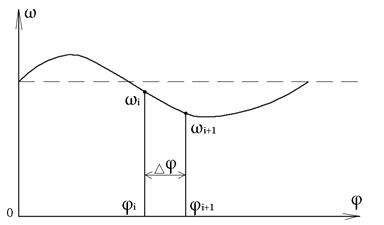
С помощью (19) и диаграммы энергомасс найдем искомую функцию ω = f(φ). Положим она выглядит таким образом:

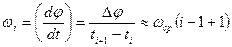
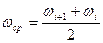подставим в верхнее и получим:

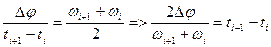
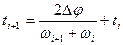
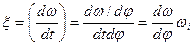
Нас интересует зависимость φ = f(t). Для ее определения воспользуемся приближенной формулой полученной таким образом:

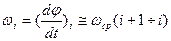
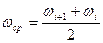подставим в верхнюю формулу

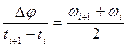
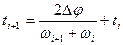(20)

Зная зависимость φ = f(t) дифференцируя, легко получим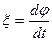

Метод конечных разностей (метод Баранова)

При использовании этого метода исходное дифференциальное уравнение движения звена приведения (см. ур-е (15)) преобразуется к разностному уравнению следующим образом:

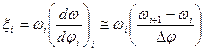
	(21)

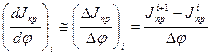
Подставляя значения 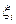; 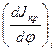из (21) в уравнение (15) и преобразовывая ее получим следующую формулу:

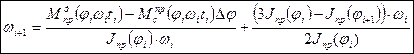(22)

При помощи (22) найдем закон движения входного звена т.к. функцию ω_i =f(φ_i) а при помощи (20) и (21) – функции φ(t) и в(φ)

2 Неравномерность движения машинного агрегата

Постановка задачи

Анализ уравнения движения МА в дифференцируемой форме показывает, что в режиме установившегося движения практически невозможно обеспечить постоянства скорости движения ведущего звена из за необходимости выполнения в каждый момент времени двух условий :

1) равенства приведенных моментов движущих сил и сил сопротивления

2) постоянства приведенного момента инерции МА.

Действительно если 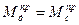и J_пр = const то уравнение (16) будет иметь вид

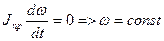(1)

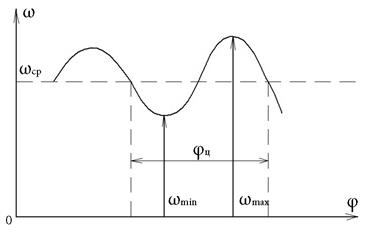
В реальных условиях эти два условия не выполняются, поэтому закон изменения угловой скорости ведущего звена в режиме установившегося движения обычно имеет вид какой то периодической функции с периодом φ_ц где ω периодически изменяется относительно постоянной ω_ср которая является желательной для данного технологического процесса

Изменение реальной скорости относительно в цикле характеризуются коэффициентом неравномерности хода б

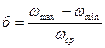(2)

Очевидно, что чем меньше б тем ближе функция ω(φ) к ω_ср = const и тем лучше выполняются условия технологических процессов и динамики движения МА. На практике принято, в зависимости от класса машин, ограничивать реальной некоторым предельным значением [б] так, чтобы в режиме установившегося движения обязательно выполнялось условие

б ≤ [б] (3)

Для реальных машин [б] изменяется в пределах 0.001-0.1 например, для самолетных двигателей [б] = 0.001; для сельхозтехмашин [б] = 0.1

Как при проектировании реальных машин обеспечить вышеупомянутое условие? Для этого воспользуемся теоремой об изменении кинетической энергии механической системы на интервале ωϵ[ω_min; ω_max]

Имеем:

∆A = ∆E ≈ 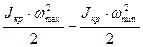(4)

Это выражение справедливо при условии 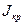≈ const которое допустимо т.к. обычно интервал [ω_min, ω_max] достаточно мал. Поэтому можно принять также следующее допущение:

ω_cр = 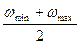(5)

Преобразуем (4)

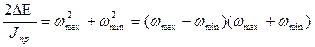(6)

Подставим в (6) , (2) и (5) получим

б 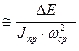(7)

Из (7) следует что для умножения б необходимо увеличивать 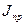так как в реальной машине ∆E и ω_ср постоянны в цикле

Поэтому определение дополнительного приведенного момента инерции 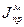машинного агрегата и является главной задачей в изучении неравномерности движения МА в режиме установившегося движения. Этот дополнительный приведенный момент инерции называется приведенный момент инерции маховых масс или маховика, а его конструктивное оформление – маховик

Методы расчета маховых масс

Определение маховых масс с помощью диаграммы энергомасс.

Это графоаналитический метод и используется тогда, когда 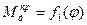; 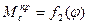и 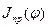– существенно переменная величина.

Положим что имеется диаграмма энергомасс, построенная для цикла. Известно, что с ее помощью можно определить угловую скорость звена приведения в i-й момент времени с помощью зависимости

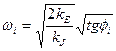
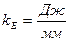
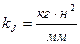
При решении задачи нам известны [б] и ω_ср, кроме того выполняется условие (3). Из (2) и (5) выразим значения ω_max и ω_min звена приведения на цикле через известные [б] и ω_ср. Получим:

ω_max = ω_ср (1+ 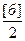) ; ω_min = ω_ср (1- 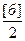) (8)

Знаем: б = 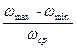(a) ω_ср = 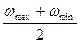(б)

ω_max = ω_min + ω_ср ∙ [б] из (б) ω_min = 2 ω_ср - ω_max тогда

ω_max = 2 ω_ср - ω_max + ω_ср ∙ [б] => 2 ω_max = 2 ω_ср + ω_ср ∙ [б]

ωmax = ωср (1+ )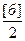

ω_min = ω_max - ω_ср ∙ [б] из (б) ω_max = 2 ω_ср - ω_min тогда

ω_min = 2 ω_ср – ω_min - ω_ср ∙ [б] => 2 ω_min = 2 ω_ср - ω_ср ∙ [б]

ωmin = ωср (1- )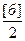

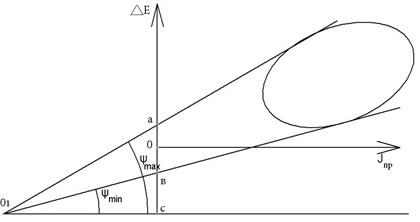
Из выражения для ω_i, используя (8) найдем значения углов ψ_max и ψ_min которые будут соответствовать ω_max и ω_min

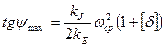
	(9)

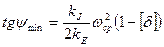
В выражениях (9) величиной ( 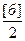)² пренебрегли, ввиду малости. Значения масштабных коэффициентов k_J, k_E берутся из графика. При экстремальных значениях угловой скорости соответствующие учи касаются диаграммы энергомасс. Проведя такие лучи под углами ψ_max и ψ_min и касаясь ими диаграммы получим изображение на графике.

Если лучи пересекутся левее оси ординат в точке O₁ , то маховик необходим и его приведенный момент будет определяться

J^н_пр = k_J ∙O₁ С кг∙м² (10)

Если точка лежит вне предела чертежа то удобнее пользоваться формулой

J^н_пр = 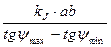(11)

Она получается из рассмотрения ∆ O₁oc и O₁bc

Определения маховых масс с помощью графиков приведенных моментов движущих сил М_g^пр и сил сопротивления М_с^пр.

В данном случае можно приближенно находить J^н_пр как в случае зависимост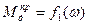и и 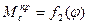, так и при функциях 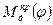и .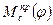

Подробнее остановимся на первом случае

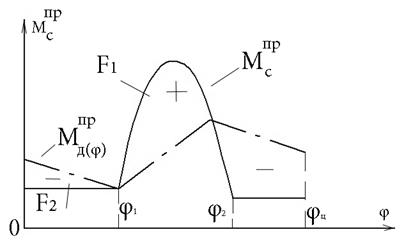
Построим заданный график зависимости 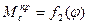за цикл

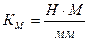
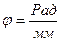
Поскольку 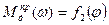, то в первом приближении построим 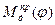в виде некоторой ломанной линии, установив при этом, что пр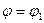и 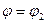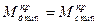и и 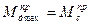соответственно, а заштрихованные со знаком (+)(+) F₁ и (-) F₂ равны. Первые два следуют из (1) , а последнее из равенства работ 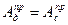в цикле. Также можно считать, что J_пр ≈ const.

Поскольку площади F₁ (или F₂) выражают избыток энергии, которая должна быть «поглощена» машины, то на основании теоремы об изменении кинетической энергии имеем.

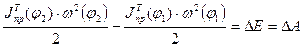(12)

Где 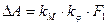(масшт. Коэфф. k_м , k_φ и площадь F₁ из графика)

На основании допущений 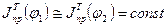( 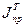- требуемый привод. Момент инерции М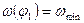А) , а 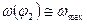, что следует из физического смысла зависимостей 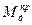, 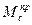и равенства (1)

Из (12) следует

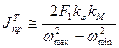
Поскольку машина уже обладает определенным 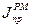, то

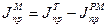(13)

Если 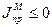, то маховик не нужен

Элементы конструирования маховика.

Если маховик необходим, то обычно его стараются совместить со звеном приведения. Как правило маховик выполняется в виде диска или кольца. Размеры этих маховиков можно определить исходя из обеспечения требуемого .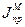

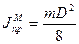- для диска

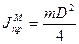- для кольца. Здесь m – масса маховика

Для уменьшения размеров маховика желательно его устанавливать на наиболее быстроходном звене. При этом необходимо пересчитать значение 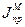по формуле:

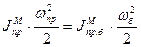
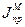, ω_ср, ω_б – известны, а 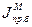определяем и далее находим новые размеры маховика.

Физический смысл «работы» маховика в накоплении и отдаче энергии

3. Основы теории автоматического регулирования машин (САР)

Постановка задачи. Основные понятия САР

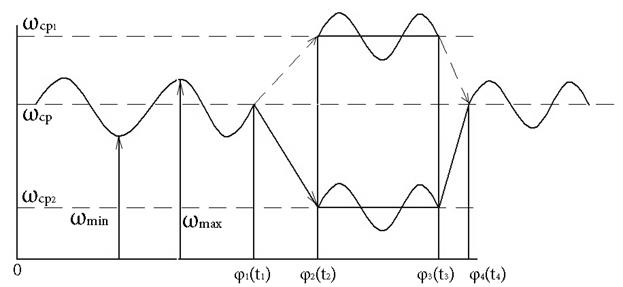
Рассмотрим установившееся движение МА. В некоторый момент времени t₁ из за случайного изменения энергии, поступаемой к машине, номинальная ω_ср за некоторый интервал 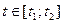становится равной ω_ср1 > ω_ср или ω_ср2 < ω_ср. Изменение ω_ср до ω_ср1 или ω_ср2 зависит от того, больше или меньше энергии от номинального значения соответственно поступило в машину, а интервал [t₁;t₂] от физических свойств машин и условий ее работы. Для нормальных условий работы МА необходимо предусмотреть в нем устройство которое бы за некоторый интервал времени возвратило его движение к прежней номинальной угловой скорости ω_ср

Исследование условий, при которых возможна такая работа машины, и составляет содержание поставленной задачи. В обзем случае возможна и точная постановка задачи когда требуется изменение по определенному закону. Все это решается с помощью САР.

Основные элементы необходимые машине с САР.

Знаем: Д – двигатель , ПМ – передаточный механизм, ИМ – исполнительный механизм

Прежде всего – это наличие обратной связи между входом и выходом

Система автоматического регулирования движения механизма

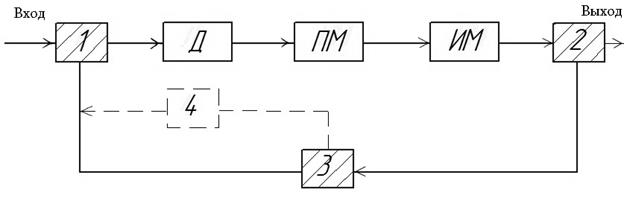
Обратную связь обеспечивает механизм 2, измеряющий выходной параметр (ω) , регулятор 3, который принимает сигнал от механизма 2, сравнивает его с эталонным и в случае их рассогласования (до определенного предела) подает соответствующий сигнал на механизмы 1. регулирующий подачу энергии к машине. Основным элементом САР является регулятор от которого зависит точность работы. Из-за этого чисто используется непрямая САР имеющая дополнительно элемент 4 – усилитель сигнала вызываемого регулятора.

В МА наиболее распространены следующие типы регуляторов скоростей:

Центробежные, инерционные, тахорегуляторы.

Более подробно рассмотрим работу машины с ц.б. регулятором.

Схема МА с центробежным регулятором скорости

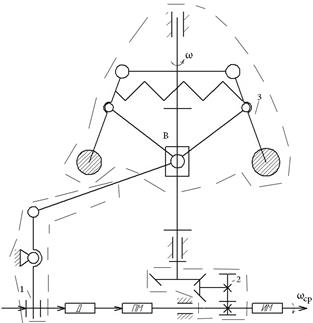
Работа регулятора

Изменения угловой скорости соответствует интервалам [t₁;t₂] ; [t₃;t₄] и характеризует динамику работы регулятора.

Для составления уравнения движения динамической модели машина с регулятором (для машин с 1 степенью свободы это нелинейное дифференциальное уравнение 3 порядка ) необходимы конкретные технические данные машины.

Поэтому динамика движения машины с САР обычно используется в спецкурсах. Однако для успешной работы машины с САР необходимо выбрать основные физико-геометрические параметры регулятора так, чтобы он двигался в соответствии с вышесказанным. Для этого необходимо рассмотреть более простую задачу – кинетостатика регулятора т.е. его равновесное состояние при некоторой постоянной угловой скорости.

Кинетостатика Ц.Б. регулятора (регулятор как бы неподвижен ω = const)

Регулятор симметричен поэтому будем рассматривать только его половину

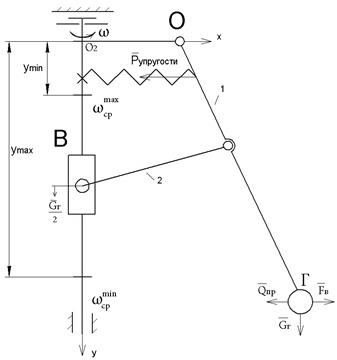
	На груз действуют
Fи = - mгaг = - mг r ω2 = f1(r)
-центробежная сила
Qпр = f (Pупр, G, Gмуфты) = f2(r)
-характеристика регулятора
1. При Fи = Qпр → r = const
2. При Fи < Qпр → r ↑ (увеличивается)
3. При Fи > Qпр → r ↓ (уменьшается)