3 страница. Здесь (-1)g – множитель для определения знака i1n, g – число внешних зацеплений
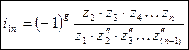 (10)
(10)
Здесь (-1)g – множитель для определения знака i1n, g – число внешних зацеплений
Частный случай: при 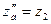 ;
; 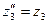 ; и т.д. получим:
; и т.д. получим:
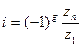 (11)
(11)
z2, z3, z4 … z(n-1) не влияют на величину передаточного отношения. Такие колеса называются паразитными (потери), а механизмы паразитным рядом.
Для уменьшения габаритов передачи
2. Планетарные механизмы (ω≥1)
Имеется хотя бы одно зубчатое колесо с подвижной геометрической осью. Такое колесо называется сателлитом.
Все планетарные механизмы делятся на две группы:
Дифференциальные механизмы (ω≥2); и планетарные передачи (ω=1)
А) Дифференциальные механизмы
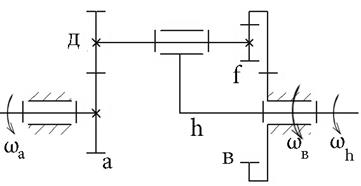
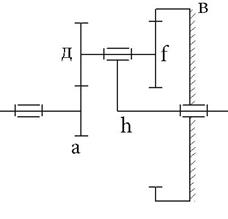
| х-х – основная ось |
| а,в – центральные колеса (солнечные колеса) | |
| g,f – сателлит (в данном случае двухвенцевой) | |
| h – водило |
Число сателлитов hw ≥ 2 (всегда) чаще nw = 3
Все сателлиты кроме одного являются пассивными звеньями и их на схеме не изображают.
а,в,h – основные звенья их признаки:
1)вращаются вокруг собственной оси
2)воспринимают нагрузки от внешних моментов
Число степеней свободы w определяется:
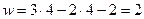 ,т.е. имеются 2-обобщенные координаты (положение звеньев будет характеризоваться углами поворота двух любых основных звеньев).
,т.е. имеются 2-обобщенные координаты (положение звеньев будет характеризоваться углами поворота двух любых основных звеньев).
Для проведения кинематического анализа диф. механизма используется метод инверсии.
Метод состоит в мысленной остановке подвижного звена механизма при сохранении относительных движений всех звеньев
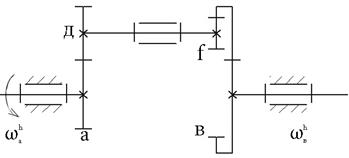
Так если всему механизму мысленно задать вращение с угловой скоростью (-ωh) , равной, но противоположной угловой скорости ωh водила h, то водило как бы , остановится, а механизм из планетарного превратится в простой рядный с неподвижными осями колес
| 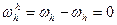
|
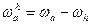
| |
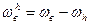
| |
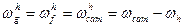
|
Учитывая (10), помня, что в данном случае одно внешнее зацепление, можно записать
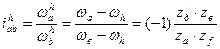 (1)
(1)
Величина 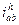 является передаточным отношением механизма с неподвижными осями полученного из планетарного остановкой водила, а формула (1) устанавливает однозначную связь между ωа ;ωв ;ωh основных звеньев с одной стороны и числом зубьев всех колес с другой. Поэтому зная любые две угловые скорости найдем третью.
является передаточным отношением механизма с неподвижными осями полученного из планетарного остановкой водила, а формула (1) устанавливает однозначную связь между ωа ;ωв ;ωh основных звеньев с одной стороны и числом зубьев всех колес с другой. Поэтому зная любые две угловые скорости найдем третью.
Аналогично можно получить передаточное отношение при остановке колеса в.
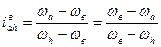 (2)
(2)
Сложим (1) и (2)
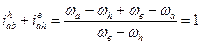 (3)
(3)
Из уравнения (1) или (2) выразим ωа , с учетом (3)
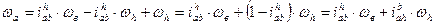
Введя индексы а → μ; в → ν; h → τ получим:
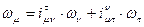 (4)
(4)
Дифференциальные механизмы применяются:
1) для функционального сложения движения
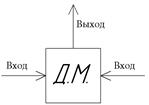
| Например, при 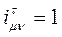 и и 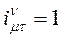
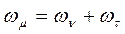
|
2) для обеспечения движения звеньев с различными скоростями при сохранении соотношения моментов на валах (например в транспортных машинах). В этом случае одно из основных звеньев (обычно водило) является входным, а два других – выходным. Не учитывая потери на трение и другие виды потерь, считая мощность на входном валу положительной, а на выходных – отрицательной, имеем
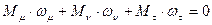 (5)
(5)
Где 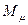 ,
, 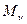 ,
, 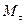 - крутящие моменты на соответствующих валах
- крутящие моменты на соответствующих валах
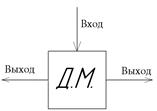
Применив метод обращения движения, мысленно остановим звено τ из (5) получим:
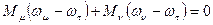
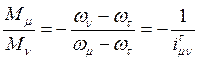
Т.е. отношение моментов на двух основных звеньях обратно пропорционально отношению их угловых скоростей относительно третьего основного звена взятого с обратным знаком.
|
2.Планетарные передачи
Образуются из дифференциальных механизмов за счет введения дополнительных связей двумя путями :
А) путем закрепления одного из центральных колес (П.П. с неподвижным солнечным колесом)
Б) путем введения дополнительной кинематической цепи, обычно зубчатой, между любыми двумя основными звеньями.
| 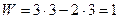
|
Тогда определим 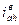 - ? - ?
| |
| Используя (3) получим | |
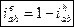 (6) (6)
| |
здесь 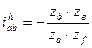
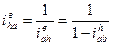 (8) (8)
|
Величина и знак 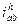 определяют кинематический эффект передачи : он особенно большой если
определяют кинематический эффект передачи : он особенно большой если 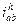 положительно и приблизительно равно 1.
положительно и приблизительно равно 1.
Покажем это на примере механизма типа «Д»
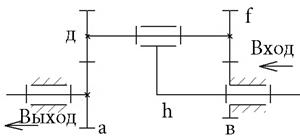
| Если: zв = 101 |
| zд = 99 | |
| Za = zf = 100 | |
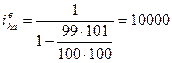 однако КПД однако КПД
|
Механизм типа «А» получается из «В» если zд = zf
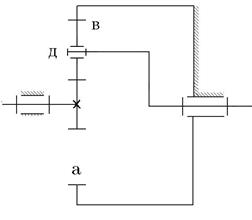
| 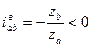 кинематический эффект небольшой кинематический эффект небольшой
|
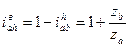
| |
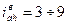
| |
| Здесь КПД выше, чем у механизма с неподвижным водилом |
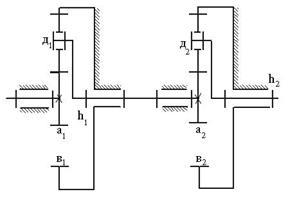
Большого кинематического эффекта при высоком КПД можно достичь последовательным соединением нескольких планетарных передач (например типа «А»)
| 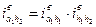
|
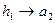
| |
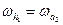
|
Передача типа «Е» (в данной передаче чаще всего za = zв)
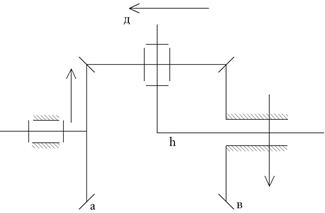
| Широко применяется в дифференциальных механизмах транспортных машин (дифференциал автомобиля) Найдем передаточное отношение при неподвижном водиле (знак находим с помощью правила стрелок) |
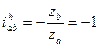 (при zb = za) (при zb = za)
| |
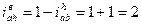
| |
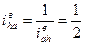
|
Механизмы ABD и E относятся к типу (2k-h) т.е. основными звеньями являются 2 центральных колеса и водило h.
Передача 3k (основными звеньями являются 3 центральных колеса а водило не является основным, так как не воспринимает нагрузку от внешних моментов, оно только поддерживает сателлиты)
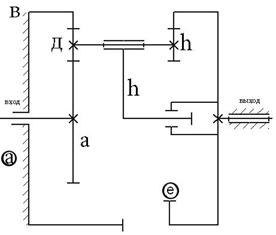
| Определим число степеней свободы. |
ω = 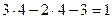
| |
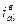 - ? - ? 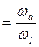
| |
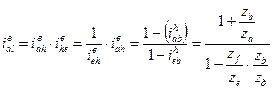
|
Очевидно, что у этой передачи можно получить большой кинематический эффект за счет знаменателя (если подбирать числа зубьев так, чтобы знаменатель → к 0). Реальное передаточное отклонение 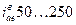
Широко применяются в планетарных рядах.
О замкнутых планетарных передачах
Для них передаточное отношение определяется их 2-х уравнений
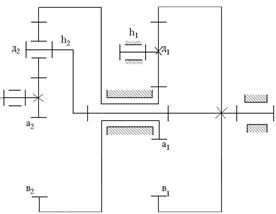
| 1)уравнение для планетарной цепи 2)уравнение для замыкающей цепи Решая совместно эти два уравнения получаем конкретное число передаточного отношения |
3. Волновые передачи
Отличительный признак – наличие в передаче хотя бы одного колеса специально деформируемого в процессе зацепления.
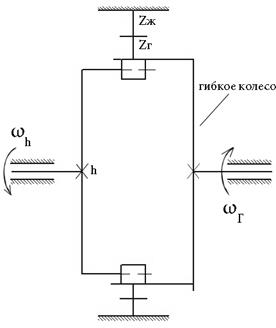
| h – генератор волн | |
| Для двухволнового генератора zm-zn=2 (min разность) | ||
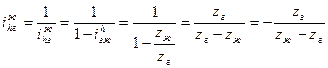
| ||
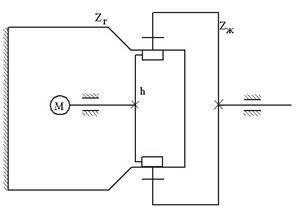
| 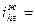 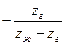
| |
| Если неподвижно гибкое колесо: | ||
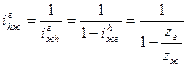
| ||
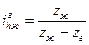
|
Достоинства:
1. Высокий кинематический эффект.
2. Высокий КПД.
3. Простота монтажа
4. Плавность передачи, способность передать вращение через перегородку
Недостатки:
1. Сложность изготовления гибкого колеса
2. Относительная маломощность
3. Невозможность получения небольших передаточных отношений
4. Качество смазки, и трудность подбора материала колеса (нагрузочная цикла)
Синтез зубчатых механизмов.
Важнейшая задача синтеза обеспечить для пары колес постоянство передаточного отношения, причем не только для полного оборота,
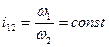 но и для бесконечно малых углов поворота
но и для бесконечно малых углов поворота
Для ступенчатых рядных механизмов
i12 > i23 > i34 и тд. (Это необходимо для уменьшения габаритов). Для планетарных механизмов необходимо дополнительно 3 условия:
1) Условие соосности (оси центровых колес и водила должны совпадать) для передач А: zа + zд = zв – zд ; Б: zа + zд = zв – zf (при равных модулях)
2) Условие соседства: вершины зубьев соседних симметрично расположенных сателлитов не должны соприкасаться (это накладывает ограничение на число сателлитов). При nw = 3– это условие выполняется автоматически.
3) Условие сборки: зубья сателлитов должны входить во впадины между зубьями центральных колес.
Для (А) => 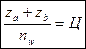 , где Ц – целое число (особо жестко для этого типа П.П.)
, где Ц – целое число (особо жестко для этого типа П.П.)
(В), (Д), ЗК => 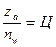 ;
; 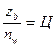 ;
; 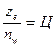
Основной закон зацепления
Отмечалось, что важнейшей задачей синтеза является обеспечение
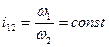 в этом случае
в этом случае 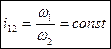
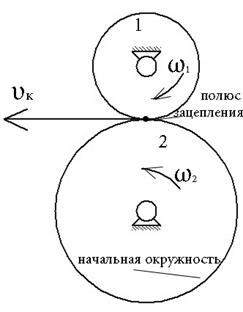
| ω (полюс зацепления) он один для заданного i |
Пусть передача вращения осуществляется звеньями с профилями П1 и П2
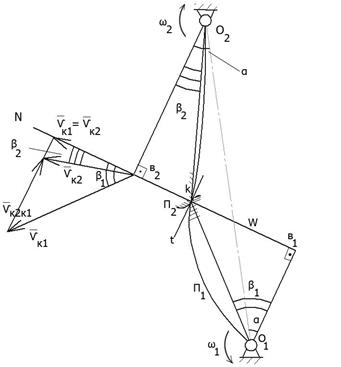
| Точка К – точка контакта t-t – общая касательная к профилю N-N – общая нормаль, пересекает линию центров О1О2 в некоторой точке W |
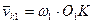 и и 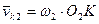 Проекции этих скоростей на N-N должны быть одинаковыми (условие правильного зацепления)
Проекции этих скоростей на N-N должны быть одинаковыми (условие правильного зацепления)
| |
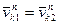
| (1) |
Действительно, другого быть не может, если 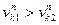 , то профиль 1 врезается в 2, если , то профиль 1 врезается в 2, если 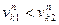 то профиль 1 не касается 2.
Скорость то профиль 1 не касается 2.
Скорость 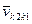 || t-t характеризует скольжение профилей П1 и П2 || t-t характеризует скольжение профилей П1 и П2
|
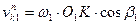 ;
; 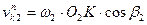
Мы видим, что 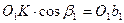 ;
; 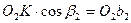
С учетом равенства (1) получим
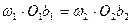
Или
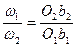
| (2) поскольку ∆b2O2W подобен ∆b1O1W
То 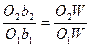 тогда тогда
|
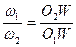
| (3) – основной закон зацепления |
- Общая нормаль N-N к профилям П1П2 в точке контакта К делит линию центров О1О2 (внешним или внутренним образом) в отношении обратном отношению угловых скоростей.
Другими словами: если мы хотим чтобы i12 = const, то общая нормаль в точке касания профилей всегда должны проходить через заданный полюс зацепления W.
Кроме этого основного кинематического требования , при выборе кривых П1 и П2 необходимо учитывать и другие:
А) Динамические (зубья должны иметь достаточную прочность и передавать постоянную мощность без резких изменений усилий)
Б) Технологические (зубчатые колеса должны быть просты в изготовлении)
В) Эксплуатационные (передачи должны быть долговечными, простыми в монтаже, бесшумными и компактными).
В качестве кривых образующих профиль зубчатых колес используется циклоидальные кривые, дуги окружности, но такие кривые используются редко т.е. сложны в изготовлении и чувствительны к ошибкам сборки, являются парными т.е. работают в одном сочетании чисел зубьев.
Эвольвенты окружностей – колеса с такими зубьями наиболее просты в изготовлении и непарные. Передачи мало чувствительные к ошибкам изготовления и сборки. Поэтому в настоящее время наиболее широко применяемы.
Дадим понятие эвольвенты окружности
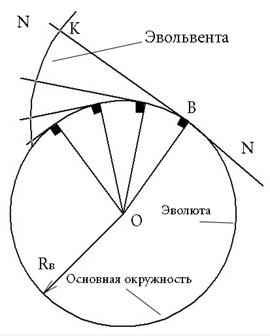
| Важные свойства эвольвенты: 1.Все точки эвольвенты, кроме одной, находятся вне основной окружности. 2. Точка В является мгновенным центром скоростей прямой N-N и центром кривизны эвольвенты в точке K, т.е. N-N является нормалью KB – радиус кривизны. 3. Форма эвольвенты зависит только от радиуса основной окружности , чем больше радиус тем меньше кривизны эвольвенты. Поэтому рейка эвольвентного зацепления имеет трапецеидальный профиль. |
Сущность эвольвентного зацепления можно продемонстрировать на примере перематывания нити (нерастяжимой) с барабана на барабан.
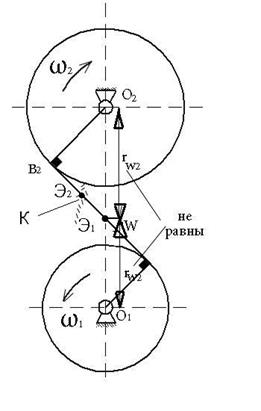
| Любая точка К на отрезке b1b2 имеет постоянную скорость 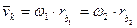 при ω1 = const, ω2 = const
Но если рассмотреть движение точки K в координатах системы жестко связанных с барабаном то она будет описывать эвольвенты Э1 и Э2 которые различны если при ω1 = const, ω2 = const
Но если рассмотреть движение точки K в координатах системы жестко связанных с барабаном то она будет описывать эвольвенты Э1 и Э2 которые различны если 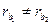 . В любой момент эвольвенты касаются друг друга и имеют общую нормаль. N-N по которой и движется точка K. При изменении O2O1 . В любой момент эвольвенты касаются друг друга и имеют общую нормаль. N-N по которой и движется точка K. При изменении O2O1 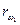 и и 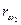 меняются, но не изменяется форма эвольвенты и величина меняются, но не изменяется форма эвольвенты и величина
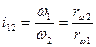
|
Основные параметры прямозубых цилиндрических колес
1. dн – начальная окружность (касание в полюсе зацепление (.) W)
2. dосн – dнcosα - диаметр основной окружности
3. α – угол зацепления 20о
4. Pt – шаг зацепления по делительной окружности
5. m – модуль зацепления
6. окружности выступов и впадин (da, df)
7. коэффициент перекрытия
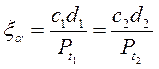
Для гарантированного безударного зацепления необходимо чтобы 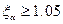 , чем больше
, чем больше 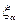 тем выше плавность работы передачи.
тем выше плавность работы передачи. 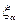 численно равен среднему числу пар зубьев одновременно находящихся в зацеплении
численно равен среднему числу пар зубьев одновременно находящихся в зацеплении
Косозубые передачи с параллельными осями валов.
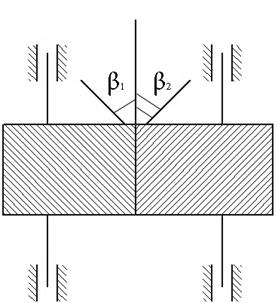
| В косозубых передачах с параллельными осями валов углы наклона винтовой линии зуба к начальному цилиндру должны быть равны по величине и противоположны по направлению 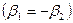 для внешнего зацепления и одинаковы для внешнего зацепления и одинаковы 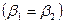 для внутреннего. В машиностроении как правило для внутреннего. В машиностроении как правило 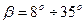
|
Кинематические зависимости для косозубых колес такие же как и для прямозубых
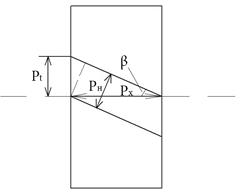
В соответствии с расположением секущей плоскости на косозубом колесе различают торцевой Pt, нормальный Pn, и осевой Px шаги и соответствующие им модули mt, mn и mx cвязь между которыми очевидна.
| 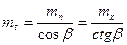
|
В торцевом сечении геометрия зацепления косозубых колес аналогична геометрии зацепления прямозубых
Коэффициент перекрытия косозубых передач больше чем у прямозубых
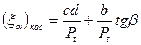
КПД косозубых передач примерно такой же как и у прямозубых. Изготавливаются теми же инструментами, но с поворотом заготовки на угол .
Недостаток - дополнительная осевая сила, возникающая при работе. Можно ликвидировать - сделать шевронный зуб, однако это сложно.
Конические зубчатые передачи
Применяются для передачи вращения между валами оси которых пересекаются под некоторым углом 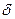 , как правило
, как правило 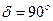
Для пары конических колес передаточное число обычно назначают для понижающих передач 1 ≤ u ≤ 6,3 для повышающих передач 1 ≤ u ≤ 3,2. КПД передачи обычно 0,98-0,96
При высоких угловых скоростях вместо прямозубых конических колес используют более сложные в изготовлении конических колеса с косыми, дуговыми или спиральными зубьями, которые работают более плавно за счет увеличенного коэффициента перекрытия.
Тема №7 Винтовые механизмы
Предназначены для преобразования вращательного движения в поступательное, причем поступательное движение может выполняться с очень высокой точностью. Звено, выполняющее поступательное движение, движется, как правило, с небольшой скоростью. Используются в механизмах, где необходимо обеспечить достаточно высокую точность позиционирования звена движущегося поступательно.
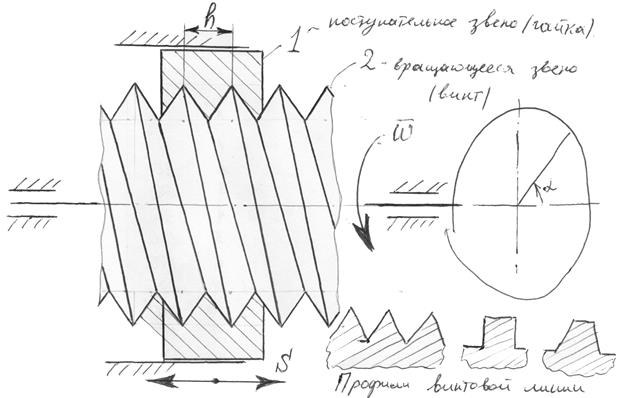
Подвижность винтового механизма определяется:
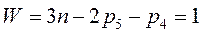
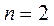 ;
; 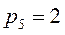 ;
; 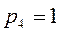
Перемещение поступательного звена, если 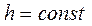 (шаг винта), определяется
(шаг винта), определяется
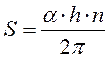
Где 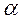 – угол поворота винта,
– угол поворота винта, 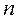 – число полных оборотов винта.
– число полных оборотов винта.
Учитывая, что 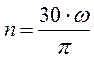 перемещение
перемещение 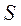 определяется
определяется
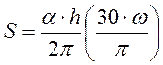
Скорость перемещения поступательного звена легко определяется. 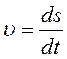
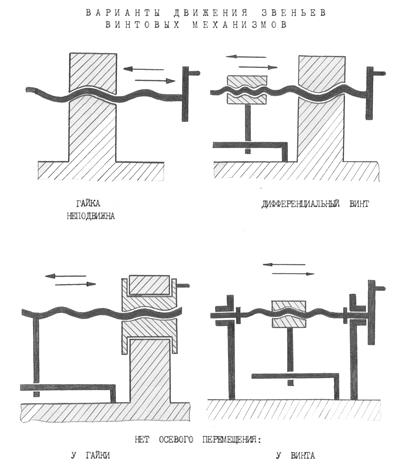
Усилие, передаваемое винтовой передачей, может достигать значительных усилий, но велики потери на трение в паре. Поступательное движение может выполнять как гайка так и винт (см. рис).
Пара “гайка-винт” образуют кинематическую пару 4 класса имеющую две степени свободы одна из которых поступательное движение звеньев друг относительно друга. Поэтому для уменьшения трения и “заедания” в месте контакта необходим подбор материалов винта и гайки. Как правило используются пары “сталь-сталь”, “сталь-бронза” , “сталь-латунь” и т.п.
Профиль винтовой линии выполняется, как правило, треугольным или прямоугольным, в зависимости от назначения механизма.
Для значительного уменьшения трения в винтовой паре используется шарико-винтовой механизм
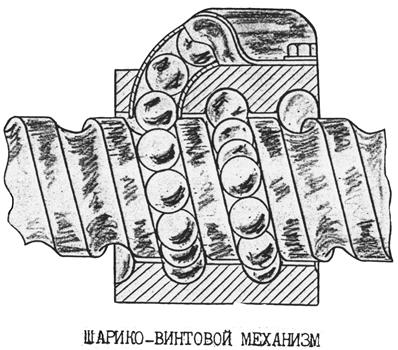
В данном случае трение скольжения 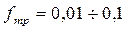 заменяется трением качения
заменяется трением качения 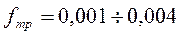 .
.
В качестве тел качения используют стальные шарики высокой твердости и различного диаметра. Как правило используются стандартные шарики, применяемые в шарикоподшипниках. Смазка пары выполняется консистентной или жидкой смазкой, в зависимости от условий работы механизма.
Недостатком винтовых механизмов является то, что они преобразуют вращательное движение в поступательное. Обратное преобразование – поступательное во вращательное, возможно только в случае очень большой величины шага 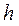 винтовой линии, но в этом случае потери будут велики, что приведет к значительному уменьшению к.п.д.
винтовой линии, но в этом случае потери будут велики, что приведет к значительному уменьшению к.п.д.
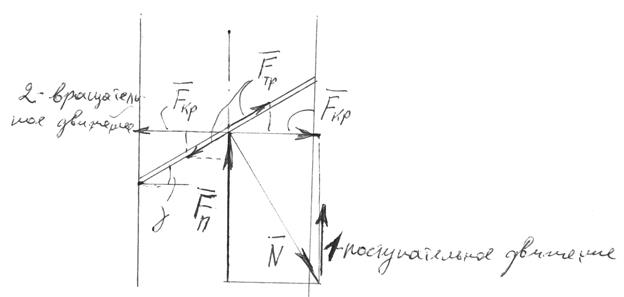
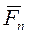 - полезная (движущая сила):
- полезная (движущая сила):
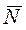 - реакция. С ростом угла
- реакция. С ростом угла 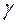 ,
, 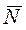 увеличивается, следовательно
увеличивается, следовательно 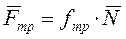 тоже возрастает следовательно уменьшается действие силы
тоже возрастает следовательно уменьшается действие силы 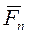 , при уменьшении угла
, при уменьшении угла 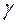 уменьшается значение
уменьшается значение 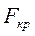 – определяющей крутящий момент на звене 2 и ее значение, при определенном значении
– определяющей крутящий момент на звене 2 и ее значение, при определенном значении 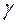 будет равно
будет равно 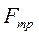 – вращение станет невозможным.
– вращение станет невозможным.
Шариковинтовая передача более сложна в изготовлении т.к. необходимо обеспечить высокую точность изготовления винтовых профильных канавок на винте и гайке. Кроме того разноразмерность шариков по диаметру не должна превышать 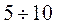 мкм.
мкм.
Дата добавления: 2015-06-17; просмотров: 947;
