Включение и выключение реальной индуктивной катушки при постоянном напряжении источника
Каждая реальная катушка индуктивности характеризуется двумя параметрами - активным сопротивлением R и индуктивностью L.
Включение катушки в электрическую сеть. Если присоединить реальную катушку к источнику постоянного напряжения (рис. 135 ), то из-за изменения тока в ходе переходного процесса в катушке возникает эдс самоиндукции 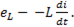
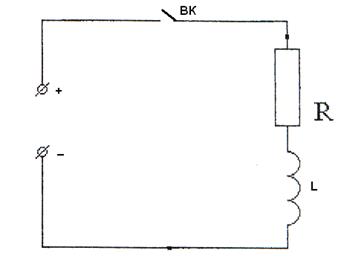
Рис.
Уравнение электрического состояния электрической цепи имеет вид:
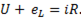 (11-15)
(11-15)
Подставим вместо 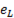 ее значение, получим
ее значение, получим
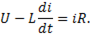
Разделим это равенство на R:
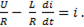 (11-16)
(11-16)
После окончания переходного процесса эдс самоиндукции будет отсутствовать, так как катушка подключена к источнику постоянного напряжения. Тогда отношение 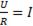 определит значение установившегося тока.
определит значение установившегося тока.
Отношение 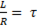 имеет размерность времени:
имеет размерность времени:
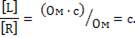
Выражение (11-16) можно переписать в виде
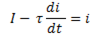
или
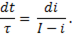
Это уравнение представляет собой дифференциальное уравнение, отражающее характер изменения тока в цепи во время переходного процесса. Проинтегируем это уравнение
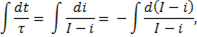
откуда следует
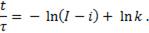
Значение постоянной интегрирования 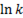 определим из начальных условий. В момент включения цепи (t = 0) ток в цепи также равен нулю (I = 0). Следовательно,
определим из начальных условий. В момент включения цепи (t = 0) ток в цепи также равен нулю (I = 0). Следовательно, 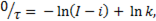 откуда
откуда 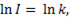 т.е.
т.е. 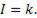
Таким образом,
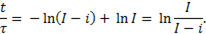
Освобождаясь от логарифмов, получим
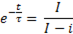
или
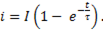 (11-17)
(11-17)
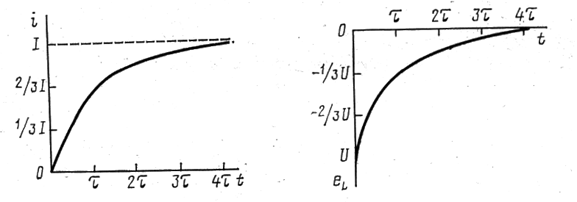
а б
Рис. 136
Это уравнение есть решение дифференциального уравнения (11-16), из которого следует, что ток в цепи при переходном процессе изменяется по экспоненциальному закону.
Из графика 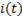 (рис. 135а) видно, что практически переходный процесс заканчивается через 4-5
(рис. 135а) видно, что практически переходный процесс заканчивается через 4-5 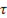 . Очевидно, что чем меньше индуктивность катушки, тем меньше постоянная времени, а следовательно, и время переходного процесса, и наоборот.
. Очевидно, что чем меньше индуктивность катушки, тем меньше постоянная времени, а следовательно, и время переходного процесса, и наоборот.
Рассмотрим, как меняется эдс самоиндукции при переходном процессе и построим график 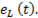 (рис. 136б).
(рис. 136б).
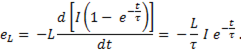
Так как 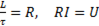 , то в окончательном виде
, то в окончательном виде
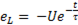 . (11-18)
. (11-18)
Минус в формуле ( ) означает, что эдс самоиндукции находится в противофазе к приложенному напряжению. Из графика 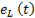 видно, что эдс самоиндукции в момент включения максимальна (
видно, что эдс самоиндукции в момент включения максимальна ( 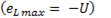 и затем спадает по экспоненциальному закону.
и затем спадает по экспоненциальному закону.
Анализируя полученные выражения можно увидеть, что функция 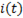 при переходном процессе зависит от приложенного напряжения
при переходном процессе зависит от приложенного напряжения 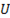 и от постоянной цепи
и от постоянной цепи 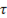 , т. е. от параметров цепи
, т. е. от параметров цепи 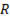 и
и 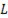 . Приложенное напряжение определяет величину установившегося тока, к которой стремится ток цепи в процессе становления, и поэтому чем больше приложенное напряжение, тем больше установившийся ток в цепи. Однако величина
. Приложенное напряжение определяет величину установившегося тока, к которой стремится ток цепи в процессе становления, и поэтому чем больше приложенное напряжение, тем больше установившийся ток в цепи. Однако величина 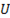 не влияет на характер кривой
не влияет на характер кривой 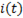 , зависящей только от
, зависящей только от 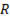 и
и 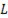 .
.
Следует отметить, что ток в цепи за время 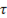 от момента включения достигает почти 2/3 своего установившегося значения.
от момента включения достигает почти 2/3 своего установившегося значения.
Параметры 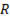 и
и 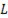 практически определяют время переходного процесса. Чем больше
практически определяют время переходного процесса. Чем больше 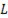 , тем больше
, тем больше 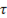 , а следовательно и продолжительность переходного процесса. Обратная картина получается при изменении сопротивления резистивного элемента.
, а следовательно и продолжительность переходного процесса. Обратная картина получается при изменении сопротивления резистивного элемента.
Отключение катушки от источника постоянного напряжения. Положим, что катушка индуктивности отключается от источника постоянного напряжения и замкнута накоротко (рис.137).
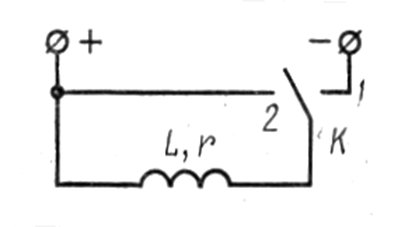
Рис. 137
При отключении источника ( 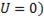
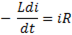
или
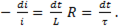 (11-19)
(11-19)
Получили дифференциальное выражение для цепи катушки, замкнутой накоротко.
Вследствие наличия магнитного поля индуктивной катушки ток в момент размыкания цепи исчезает не мгновенно, так как эдс самоиндукции, обусловленная убыванием магнитного потока, стремиться поддержать ток. При этом эдс самоиндукции изменяет свой знак, так как она обусловлена уже не нарастанием потока, как это было при включении цепи, а его убыванием. Это приводит к тому, что в первое мгновение разрыва цепи напряжение между расходящимися контактами резко увеличивается до величины 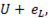 благодаря чему между контактами возникает искровой разряд, который при значительной мощности может переходить в дуговой.
благодаря чему между контактами возникает искровой разряд, который при значительной мощности может переходить в дуговой.
Искровой, а тем более дуговой разряд нарушает чистоту контактов и разрушает их. Для устранения разряда, отключающие аппараты, как правило, снабжаются специальными устройствами для гашения дуги ( например, катушку при размыкании цепи замыкают на резистор).
При замыкании катушки на разрядной сопротивление R, вследствие наличия магнитного поля катушки ток в цепи после ее разрыва не может исчезнуть мгновенно. Его изменение зависит от параметров цепи, и переходный процесс длится до тех пор, пока сохраняется энергия в магнитном поле катушки. По мере того как энергия магнитного поля рассеивается, преобразуясь в тепловую энергию на сопротивлении R, ток в контуре стремиться к нулю.
Второй закон Кирхгофа при размыкании цепи запишется в виде
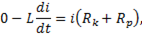
где 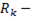 активное сопротивление катушки,
активное сопротивление катушки, 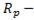 разрядное сопротивление.
разрядное сопротивление.
Обозначив 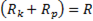 , где
, где 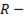 активное сопротивление цепи, уравнение ( ) перепишем следующим образом:
активное сопротивление цепи, уравнение ( ) перепишем следующим образом:
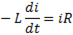
или
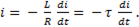
Разделив переменные, получим
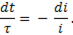
Проинтегрируем это выражение
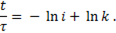
Постоянную интегрирования определим из начальных условий. В момент разрыва цепи
(t = 0) ток в цепи равен установившемуся току, т.е. 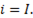
При t = 0 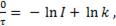 откуда
откуда 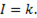 Тогда
Тогда
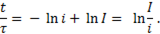
Следовательно,
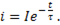 (11-20)
(11-20)
Из этого выражения следует, что ток в цепи с разрядным сопротивлением (рис.138) изменяется по убывающей экспоненте.
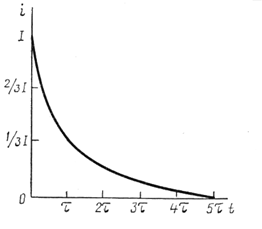
Рис.138
Дата добавления: 2015-06-17; просмотров: 12237;
