ПЕРЕДАЧА ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ ПО ПРОВОДАМ

Для практики большое значение имеет то, что одну и ту же мощность можно по проводам передать при низком напряжении и большом токе или при высоком напряжении и малом токе.

Согласно, представленной схемы (рис.22),

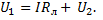(2-43)

Умножим это уравнение на величину тока, преобразовав его в уравнение мощностей

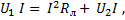(2-44)

где 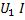- мощность генератора электрической энергии,I² R_л- потеря мощности в проводах линии, U₂I –мощность потребляемая нагрузкой.

Если повысить напряжение на зажимах нагрузки в 100 раз (U₂^*=100U₂), то, чтобы получить ту же мощность, нужно уменьшить в 100 раз ток, т.е. до значения I^*=I/100. Тогда потери в проводах линии (при неизменном R_л) уменьшаются в 10 000раз, т.к.

I^*2 R_л = I ²R_л/10 000.

Следовательно, при повышении напряжения в десять раз и, если сохранить процент потерь мощности при передаче энергии неизменным, можно уменьшить площадь сечения проводов линии в 10 000 раз или удлинить линию в 10 000 раз.

Или другой оценочный пример.

Пусть генератор на электростанции имеет мощность Р = 200МВт=2 10⁸Вт. Оценим диаметр медного провода при передаче этой энергии при напряжениях 100В и 1МВ=10⁶В.

При напряжении 100В для передачи такой мощности требуется ток в I=P/U =2 10⁶А, а при напряжении 10⁶В величина тока равна 200А.

Максимальная плотность тока для меди составляет величину порядка

j = I/S = 2А/мм².

Тогда, в первом случае, сечение и диаметр медного провода составляют величины порядка 1м² и 1м, соответственно. Во втором случае, эти величины 10^-4 м² и 10^-2м, соответственно.

Сравнение этих значений свидетельствует о том, что передача электрической энергии экономически более выгодна при повышенном напряжении. Это и применяется на практике с использованием высоковольтных линий электропередач (ЛЭП).

Кроме того, следует учитывать и большие тепловые потери при протекании больших токов при передаче электрической энергии.