Линеаризованная модель биполярного транзистора
Используя формальную запись нелинейных зависимостей
Iк= F(Iб, Uкэ),
Uбэ= F(Iб, Uкэ) (4.7)
и разлагая (4.7) в ряд Тейлора относительно некоторого режима покоя
Iб0, Iк0, Uкэ0, Uбэ0
получим линеаризованное уравнение
 ,
,
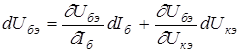 .
.
Или, вводя обозначения,
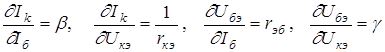 ,
,
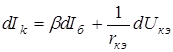 ,
, 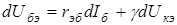 . (4.8)
. (4.8)
Физический смысл коэффициентов линеаризованного уравнения (4.8) вытекает из математических соотношений
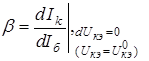 - дифференциальный коэффициент усиления тока базы;
- дифференциальный коэффициент усиления тока базы;
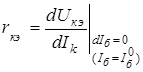 - дифференциальное выходное (внутреннее) сопротивление;
- дифференциальное выходное (внутреннее) сопротивление;
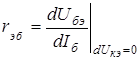 - дифференциальное входное сопротивление;
- дифференциальное входное сопротивление;
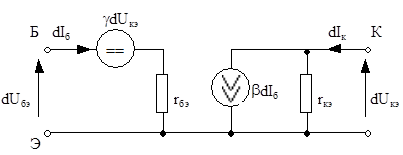 Рис. 4.12. Линеаризованная электрическая модель биполярного транзистора
Рис. 4.12. Линеаризованная электрическая модель биполярного транзистора
|
 - коэффициент обратной связи по напряжению.
- коэффициент обратной связи по напряжению.
Уравнениям (4.8) соответствует электрическая схема, которая и является линеаризованной моделью биполярного транзистора (рис. 4.12).
Параметры линеаризованной модели зависят от режима покоя, поэтому в справочных данных они приводятся для конкретного режима и для другого режима должны быть пересчитаны, определены экспериментально или графически по ВАХ.
В технической литературе уравнение (4.8) часто приводятся в системе h-параметров (из теории электрических четырехполюсников):
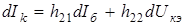 ,
, 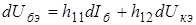 (4.9)
(4.9)
Из (4.8) и (4.9) очевидны значения и смысл h-параметров.
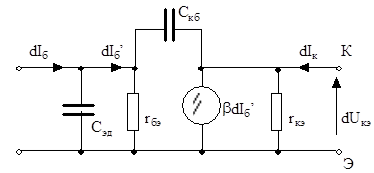 Рис. 4.13. Линеаризованная модель биполярного транзистора, учитывающая инерционность
Рис. 4.13. Линеаризованная модель биполярного транзистора, учитывающая инерционность
|
Инерционность биполярного транзистора в активном режиме можно определить введением диффузионной емкости открытого эмиттерного перехода Сэд и зарядной емкости коллекторного перехода Скз (рис. 4.13), где для упрощения принято g=0.
Следует еще раз подчеркнуть, что практическое использование даже линеаризованных моделей для ручного расчета приводит к достаточно сложным аналитическим выражениям, поэтому следует рекомендовать в качестве основного способа анализа - цифровое моделирование.
Дата добавления: 2015-06-17; просмотров: 801;
