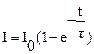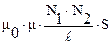Токи при размыкании и замыкании цепи
Пусть ключ SA замкнут и в цепи (рисунок 33) течет ток 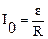 .
.
|
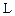 начнет уменьшаться, и появится ЭДС самоиндукции
начнет уменьшаться, и появится ЭДС самоиндукции 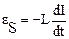 .
.
По закону Ома 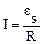 . Отсюда :
. Отсюда : 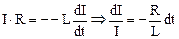 .
.
|
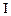 (от
(от 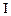 0 до
0 до 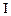 ) и по
) и по 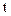 (от 0 до
(от 0 до 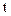 ), получим:
), получим: 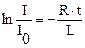 или:
или:
Здесь 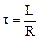 - постоянная, называемая временем релаксации, т.е. временем за которое сила тока
- постоянная, называемая временем релаксации, т.е. временем за которое сила тока 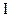 уменьшится в "е" раз.
уменьшится в "е" раз.
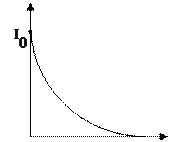 Чем больше
Чем больше 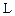 , тем больше t и тем медленнее убывает ток по экспоненциальному закону (рисунок 34).
, тем больше t и тем медленнее убывает ток по экспоненциальному закону (рисунок 34).
|
|
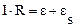 ;
; 
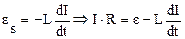
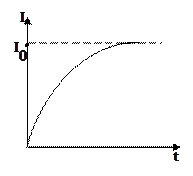 Обозначим:
Обозначим: 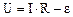 , тогда
, тогда 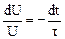 . Интегрируя это выражение по
. Интегрируя это выражение по 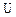 (от
(от 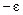 до
до 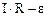 ) и
) и
|
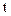 (от 0 до
(от 0 до 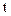 ), получим:
), получим:
|
Ток нарастает по экспоненциальному закону(рисунок 35).При 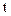 = 0Þ
= 0Þ 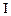 = 0.
= 0.
Взаимная индукция
Рассмотрим два неподвижных контура (1 и 2), расположенных близко друг от друга с токами 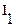 и
и 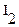 соответственно (рисунок 36). Часть потока от тока
соответственно (рисунок 36). Часть потока от тока 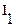 , которая пронизывает контур 2:
, которая пронизывает контур 2:
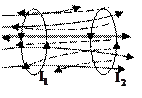 |
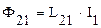 ;
; 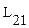 – коэффициент пропорциональности.
– коэффициент пропорциональности.
|
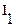 меняется, то в контуре 2 индуцируется ЭДС:
меняется, то в контуре 2 индуцируется ЭДС: 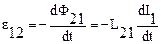 .
.
Аналогично при протекании в контуре 2 тока 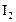
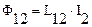 - часть потока от тока
- часть потока от тока 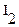 , пронизывающего контур 1 и
, пронизывающего контур 1 и 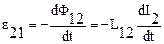 .
.
Явление возникновения ЭДС в одном контуре при изменении силы тока в другом контуре называется взаимной индукцией.
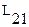 и
и 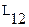 - называются коэффициентами взаимной индуктивности контуров. Расчеты показывают, что
- называются коэффициентами взаимной индуктивности контуров. Расчеты показывают, что 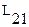 =
= 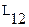 .
. 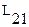 и
и 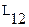 зависят от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей среды.
зависят от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей среды.
Коэффициент взаимной индуктивности двух катушек, намотанных на общий тороидальный сердечник:
|
, где 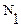 – число витков
– число витков
первичной обмотки; 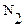 – число витков вторичной обмотки;
– число витков вторичной обмотки;
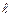 – длина сердечника по средней линии;
– длина сердечника по средней линии;
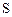 – площадь поперечного сечения сердечника.
– площадь поперечного сечения сердечника.
Дата добавления: 2015-06-12; просмотров: 990;

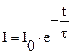 .
.