Разряд конденсатора через сопротивление
Рассмотрим электрическую цепь, состоящую из конденсатора емкостью С и сопротивления R, соединенных с источником тока как показано на рис. 1.
 1 К 2
1 К 2
С R
Е
Рис. 1
С помощью ключа К конденсатор присоединяется к источнику напряжения и заряжается. Обозначим напряжение на обкладках конденсатора 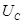 . Если теперь ключ К повернуть в положение (2), то конденсатор начнет разряжаться через сопротивление R, напряжение на обкладках конденсатора постепенно спадает до нуля. Ток в цепи, начиная от нуля, быстро достигает максимального значения
. Если теперь ключ К повернуть в положение (2), то конденсатор начнет разряжаться через сопротивление R, напряжение на обкладках конденсатора постепенно спадает до нуля. Ток в цепи, начиная от нуля, быстро достигает максимального значения 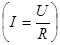 , а затем уменьшается до нуля. Весь этот процесс длится небольшой промежуток времени (доли секунды), величина которого зависит от величины сопротивления R и емкости C конденсатора.
, а затем уменьшается до нуля. Весь этот процесс длится небольшой промежуток времени (доли секунды), величина которого зависит от величины сопротивления R и емкости C конденсатора.
Такой процесс, когда при замыкании цепи величина тока устанавливается не сразу, а постепенно, называется переходным. Запишем второй закон Кирхгофа для цепи, содержащей конденсатор С и сопротивление R:
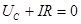 (1)
(1)
Так как 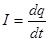 , а
, а 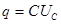 , то
, то 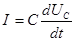 (2)
(2)
Подставив выражение (2) в уравнение (1), получим дифференциальное уравнение первого порядка:
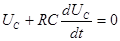 или
или
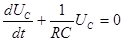 (3)
(3)
Решение этого уравнение имеет вид:
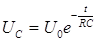 , (4)
, (4)
где 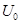 - напряжение на обкладках конденсатора в начальный момент времени (
- напряжение на обкладках конденсатора в начальный момент времени ( 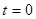 ). Произведение
). Произведение 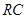 , стоящее в показателе степени имеет размерность времени и называется постоянной временицепи с
, стоящее в показателе степени имеет размерность времени и называется постоянной временицепи с 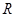 и С, обозначается
и С, обозначается 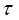 :
:
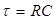
Тогда уравнение (4) перепишется:
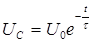 (5)
(5)
Уравнение (5) выражает закон изменения напряжения со временем на обкладках конденсатора при его разряде.
Выясним физический смысл постоянной 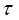 времени. Если
времени. Если 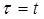 , то
, то 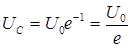 или
или 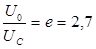 .
.
Следовательно, постоянная времени 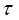 - это промежуток времени, за который напряжение на обкладках конденсатора при разряде уменьшается в
- это промежуток времени, за который напряжение на обкладках конденсатора при разряде уменьшается в 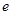 раз.
раз.
Величина, обратная 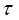 ,
, 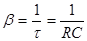 называется коэффициентом затухания.
называется коэффициентом затухания.
Коэффициент затухания 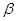 характеризует скорость уменьшения напряжения при разряде конденсатора. Чем больше R и С, тем меньше
характеризует скорость уменьшения напряжения при разряде конденсатора. Чем больше R и С, тем меньше 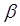 , т.е. тем медленнее происходит разряд конденсатора.
, т.е. тем медленнее происходит разряд конденсатора.
Дата добавления: 2015-06-12; просмотров: 3417;
